Attack Kab Review
22 Sep 2025Attacking Knowledge Acquisition Bottleneck: frameworks, algorithms and applications
1. Introduction
The Knowledge Acquisition Bottleneck (KAB) represents a fundamental and pervasive challenge across artificial intelligence (AI), significantly impeding the development of truly autonomous and intelligent systems. Historically, the KAB emerged prominently in the 1970s and 80s with early expert systems, characterized by the prohibitive manual effort, reliance on human experts, and substantial cost associated with hand-encoding knowledge into formal, rule-based representations [52,59,75]. This foundational problem persists, having evolved in complexity and manifestation with successive advancements in AI paradigms [47].
In contemporary AI, a comprehensive definition of the KAB incorporates the challenge of “dynamic knowledge integration” and the critical distinction between “acquired” and “utilized” knowledge, especially evident in modern Pre-trained Language Models (PLMs). While PLMs acquire vast amounts of parametric knowledge during pre-training, a significant “knowledge acquisition-utilization gap” exists, where the mere presence of knowledge within a model’s parameters does not guarantee its effective and flexible deployment in downstream tasks [34,53]. This gap is further exacerbated by the static nature of deployed LLMs, which struggle to dynamically update and adapt to constantly evolving information, frequently leading to outdated knowledge, hallucinations, and overall unreliability in knowledge-intensive applications [5,20,27,36]. Dynamic knowledge integration, therefore, refers to an AI system’s ability to continuously learn, update, and reconcile new information with its existing knowledge base, a capability still largely nascent in current static models [67].
The pervasive nature of the KAB is evident across various AI subfields, manifesting in distinct yet interconnected ways, each defined by specific underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations. For instance, in Knowledge Representation (KR) and Knowledge Graph (KG) construction, the KAB is marked by extensive manual effort, data scarcity, semantic heterogeneity, and scalability issues [3,23,55]. In contrast, robotics faces KABs related to interpreting sensor data, engineering explicit models for physical interactions, tractability of planning, and the need for dynamic knowledge in variable environments [64]. For Large Language Models (LLMs), new facets of the KAB include computational cost, massive data requirements, interpretability issues concerning how knowledge is internalized, catastrophic forgetting, and ineffective knowledge injection mechanisms [7,8,12,32,34,44]. This contrasts with KGs, which, despite their accuracy and traceability, grapple with scalability and manual updating [3,40]. In Reinforcement Learning (RL), the KAB centers on efficient exploration in sparse reward environments [56], whereas in educational AI, it involves accurately modeling student knowledge and translating it into interpretable, actionable feedback for educators [22,50]. Furthermore, the KAB differentiates between constructive contexts, such as building AI for beneficial applications with challenges like data scarcity and interpretability [2,19], and adversarial contexts, exemplified by model extraction attacks against proprietary AI models [15,45].
The timeliness and significance of this survey are underscored by the critical role that effective knowledge acquisition plays in advancing AI capabilities, transforming AI from narrow, data-driven systems into more robust, interpretable, and adaptable intelligent agents [19,32,70]. The proliferation of LLMs and advancements in Natural Language Processing (NLP) have paradoxically amplified the prominence and urgency of the KAB. While LLMs exhibit expansive knowledge coverage and impressive generalization capabilities [12], they introduce new facets of the KAB related to their inherent limitations, such as outdated or static knowledge, susceptibility to hallucinations, domain-specific deficits, and poor transferability across specialized tasks [20,70]. This necessitates continuous learning and adaptation to dynamic world knowledge, a task where LLMs frequently struggle, especially in later pretraining stages where new knowledge acquisition becomes increasingly difficult, as observed through metrics like “knowledge entropy” [69]. Moreover, the growing reliance on AI in sensitive domains like healthcare and scientific discovery demands interpretability, trustworthiness, and robustness, which are often hampered by the KAB [48,50].
Beyond developing solutions, it is crucial to both understand and rigorously measure the KAB, a perspective explicitly highlighted in the context of assessing knowledge utilization in PLMs [53]. Diagnostic and analytical studies, such as those employing controlled datasets to study memorization in LLMs [60], or proposing novel metrics like knowledge entropy [69], are indispensable for guiding future research. The establishment of standardized benchmarks, exemplified by Bench4KE for automated competency question generation in Knowledge Engineering (KE) [14], is fundamental for systematic evaluation and comparison of methods addressing the KAB.
This academic survey, titled “Attacking Knowledge Acquisition Bottleneck: frameworks, algorithms and applications,” delineates the current research landscape by organizing it around several main themes: frameworks, algorithms, and applications, with a critical examination of their constructive and adversarial dimensions. The survey covers architectural designs and systematic approaches (frameworks), specific computational methods (algorithms) for diverse tasks like information extraction, skill discovery, and knowledge injection, and their applications across various domains including LLMs/NLP, robotics, game AI, and sensitive fields. It also differentiates between constructive efforts for beneficial AI and defensive strategies against adversarial knowledge acquisition, such as model extraction attacks [18,19,20,21,28,35,43,44,45,51,54,56,63,66,70].
The primary contribution of this survey is to organize the current, often fragmented, research landscape by systematically comparing, contrasting, and synthesizing insights from diverse approaches to the KAB. It explicitly identifies the underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations that contribute to the observed strengths, weaknesses, and performance differences between methods. A recurring insight, for instance, is the convergence of neuro-symbolic AI, where combining LLMs’ expansive but implicit knowledge with KGs’ structured and interpretable representations can mitigate hallucinations and enhance reasoning [12,70]. Conversely, purely fine-tuned models can often outperform LLM-based in-context learning in specific tasks, indicating a comparative weakness in generalizability for direct application [18]. Critically, the survey also assesses the limitations and potential areas for improvement. Many current solutions, while effective in specific contexts, face challenges in generalizability, scalability, computational cost, and data dependency [17,37,43,44]. Furthermore, ethical considerations, bias mitigation, and the trade-offs between model size and knowledge integration capabilities remain largely unaddressed in many specialized studies [69]. Overcoming the KAB necessitates interdisciplinary research, moving beyond isolated solutions to foster frameworks that combine diverse knowledge representations, dynamic learning mechanisms, and enhanced human-AI collaboration. This includes developing new methodologies for data-efficient learning, enabling systems to dynamically update knowledge, bridging the gap between acquired and utilized knowledge, and improving the interpretability and explainability of AI’s internal knowledge processes. By pinpointing these limitations and unaddressed questions, this survey aims to highlight future research directions that are crucial for developing more robust, efficient, and ethical AI systems.
1.1 Defining the Knowledge Acquisition Bottleneck
The Knowledge Acquisition Bottleneck (KAB) represents a fundamental and pervasive challenge across artificial intelligence (AI), impeding the development of truly autonomous and intelligent systems. Fundamentally, the KAB describes the inherent difficulties and resource-intensive processes involved in enabling AI systems to effectively acquire, integrate, represent, maintain, and apply knowledge from diverse sources for robust and generalizable performance [47]. Historically, this bottleneck first emerged prominently in the 1970s and 80s with early expert systems, characterized by the prohibitive manual effort, reliance on human experts, and cost associated with hand-encoding knowledge into formal, rule-based representations [52,59,75]. This foundational problem persists, evolving in complexity and manifestation with successive advancements in AI paradigms.
A comprehensive definition of the KAB must incorporate the challenge of “dynamic knowledge integration” and the critical distinction between “acquired” and “utilized” knowledge, especially evident in modern Pre-trained Language Models (PLMs) [34,53]. While PLMs acquire vast amounts of parametric knowledge during pre-training, there exists a significant “knowledge acquisition-utilization gap,” where the mere presence of knowledge within a model’s parameters does not guarantee its effective and flexible deployment in downstream tasks [53,68,73]. This gap is further exacerbated by the static nature of deployed LLMs, which struggle to dynamically update and adapt to constantly evolving information, frequently leading to outdated knowledge, hallucinations, and overall unreliability in knowledge-intensive applications [5,20,27,36]. Dynamic knowledge integration, therefore, refers to an AI system’s ability to continuously learn, update, and reconcile new information with its existing knowledge base, a capability still largely nascent in current static models [67].
Comparative KAB Manifestations in Paired AI Subfields
| AI Subfield Pair | Key KAB Manifestations (AI-1) | Key KAB Manifestations (AI-2) | Core Contrast/Distinction |
|---|---|---|---|
| KR & KG vs. Robotics | Manual effort, Data scarcity, Semantic heterogeneity, Scalability, Error propagation | Sensor data interpretation, Explicit physical models, Planning tractability, Dynamic knowledge, Data scarcity, Environmental variability | Structure/content of knowledge vs. Operational acquisition/application in physical environment |
| LLMs vs. Knowledge Graphs (KGs) | Computational cost, Massive data requirements, Interpretability, Catastrophic forgetting, Ineffective knowledge injection, Hallucinations, Static nature, Acquisition-utilization gap | Manual effort for construction/update, Scalability, Limited extrapolation/reasoning transferability, Data heterogeneity, Incompleteness | Implicit/broad/general vs. Explicit/structured/precise |
| Reinforcement Learning (RL) vs. Educational AI | Efficient exploration in sparse rewards, Acquiring behavioral primitives, Costly/unsafe physical exploration | Modeling student knowledge from diverse materials, Interpretable/actionable feedback, Distinguishing knowledge gain, Hallucinations in LLM explanations | Efficient policy/behavior acquisition vs. Interpretable human learning models |
| Constructive Contexts vs. Adversarial Contexts | Manual effort, Data scarcity, Scalability, Interpretability, Building beneficial AI | Model extraction attacks, Limited query budgets, Lack of domain knowledge, Ethical/security implications (IP theft) | Building AI for benefit vs. Exploiting AI for unauthorized knowledge acquisition |
The KAB’s pervasive nature is evident across various AI subfields, manifesting in distinct yet interconnected ways, each defined by specific underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations.
1. Knowledge Representation vs. Robotics:
In the realm of Knowledge Representation (KR) and Knowledge Graph (KG) construction, the KAB is historically rooted in the difficulty of creating and maintaining formal, structured knowledge. This involves extensive manual effort, cost, and reliance on human experts for knowledge elicitation, conceptualization, and formalization [3,31,52,55]. Modern KG construction still grapples with data scarcity of high-quality graph-structured data, error propagation in multi-stage pipelines, semantic heterogeneity across diverse sources, and scalability issues when dealing with large, dynamic information landscapes [23,38,40,55]. The “Open World problem” further highlights the KAB’s facet in the difficulty of distinguishing new from old knowledge and integrating it without catastrophic forgetting, especially when feature distributions differ significantly between known and unknown entities [37].
Conversely, in robotics, the KAB is deeply intertwined with embodied intelligence and real-world interaction [64]. It manifests through a complex interplay of: (1) a core Knowledge Bottleneck requiring human experts to manually interpret sensor data and provide explicit domain knowledge for tasks like object classification; (2) an Engineering Bottleneck stemming from the substantial time and effort required to implement and generate explicit models for robot dynamics and environmental interactions, especially for complex physical properties; (3) Tractability issues arising from the computational complexity of realistic planning problems, leading to slow response times; and (4) Precision challenges in executing plans with sufficient accuracy, particularly with flexible robots [64]. Additionally, data scarcity for real-world training, environmental variability with unpredictable noise, and the necessity for dynamic knowledge due to changing robot properties (e.g., wear, temperature) further amplify the KAB in robotics. While knowledge representation focuses on the structure and content of knowledge itself, robotics emphasizes the operational acquisition and application of knowledge within a physical, dynamic environment.
2. LLMs vs. Knowledge Graphs:
The KAB in Large Language Models (LLMs) contrasts sharply with that in Knowledge Graphs (KGs), highlighting fundamental differences in their knowledge paradigms [12]. For LLMs, KABs extend beyond the acquisition-utilization gap to include the computational cost and massive data requirements for pre-training, which pose significant challenges for deployment on resource-constrained systems [8]. A critical aspect is the “critical gap in understanding how LLMs internalize new knowledge” and structurally embed this acquired knowledge in their neural computations, affecting learning and retention dynamics, as quantified by concepts like knowledge entropy decay during pre-training [5,30,34,69]. This interpretability challenge extends to the lack of transparent reasoning, debugging capabilities, and control over LLM behavior, which affects reliability and safety [32]. Furthermore, LLMs face catastrophic forgetting during fine-tuning and struggle with effective knowledge injection from external KGs, sometimes treating relevant injected knowledge as noise due to ineffective knowledge utilization or knowledge complexity mismatch [7,42,44,61]. Eliciting knowledge from LLMs also presents a KAB due to manual effort in prompt engineering and the sensitivity to phrasing [43]. When integrating LLMs with structured knowledge like KGs (e.g., in Retrieval-Augmented Generation, RAG), an architectural mismatch arises because most RAG pipelines are designed for unstructured text, limiting their applicability to holistic graph structures and leading to a knowledge acquisition-utilization gap where LLMs lack substantial pre-training on graph data [1,63]. LLMs’ inherent struggle to maintain structured consistency and susceptibility to hallucinations also pose a KAB for LLM-driven ontology evolution [17].
In contrast, KGs are characterized by high accuracy, controlled reasoning, traceable origins, and human-centric interpretability [12]. However, KGs face their own KABs related to scalability (e.g., model size and inference time grow linearly with KG size), limited extrapolation, reasoning transferability, and the manual effort required for continuous updating and validation, particularly for emerging entities and relations [3,23,40,49]. LLMs’ strength in broad coverage and generalization, and KGs’ strength in structure and precision, illustrate a “cognitive gap” in how knowledge is stored and organized, highlighting the trade-off in the KAB for each paradigm [12].
3. Reinforcement Learning (RL) vs. Educational AI:
The KAB manifests distinctly in RL and educational AI, reflecting their differing learning objectives and environments. In RL, the KAB primarily concerns the difficulty of efficient exploration and knowledge acquisition in environments characterized by sparse reward signals [35,56]. Agents struggle to discover effective policies without clear and frequent reward feedback, or to acquire useful behavioral primitives for navigating vast state-action spaces. This often necessitates physical exploration, which can be costly or unsafe. The core problem is bridging the gap between minimal environmental feedback and the complex knowledge needed for optimal behavior.
Conversely, in educational AI, the KAB centers on the challenge of accurately modeling student knowledge from diverse learning materials and translating this into interpretable, actionable feedback for educators [22,50]. Traditional knowledge tracing methods exacerbate this KAB by relying on opaque, high-dimensional latent vectors, which provide limited cognitive interpretability or concrete guidance for teaching strategies. The difficulty arises from distinguishing knowledge gain from gradable versus non-gradable learning activities, and confounding factors like student selection bias [22]. LLM-based explanations, while promising, are susceptible to hallucination, hindering reliability as educational tools [50]. The KAB here is about transforming internal system representations of knowledge into human-understandable and pedagogically useful insights.
4. Constructive vs. Adversarial KAB:
The KAB also differentiates between constructive and adversarial contexts. Constructively, the KAB encompasses the traditional challenges of manual effort, data scarcity (e.g., for labeled data, specialized domain knowledge, or sense-annotated corpora), scalability (e.g., maintaining large knowledge bases, handling scientific information overload), and interpretability in building AI systems for beneficial applications [2,6,10,11,14,16,19,21,25,28,39,41,48,51,57,65,70,72]. This includes the challenge of translating scientific research into accessible knowledge or making ML models’ predictions scientifically insightful [2,39].
In contrast, an adversarial KAB describes the challenge faced by an adversary in efficiently acquiring the functional knowledge of a proprietary model (e.g., a Machine Learning as a Service (MLaaS) model) under practical constraints like limited query budgets and lack of domain knowledge [15,45]. This form of KAB involves ethical and security implications, including copyright violations, patent infringement, and financial and reputational damage to model owners. The underlying problem is reconstructing an accurate substitute model with minimal interaction.
Implications for Solutions and Future AI Systems: The diverse manifestations of the KAB across domains underscore that there is no single, universal solution; rather, a spectrum of tailored and often interdisciplinary approaches is required. Addressing this bottleneck is crucial for advancing AI systems towards greater autonomy and intelligence because it directly impacts their:
- Reliability and Trustworthiness: Systems prone to hallucinations, outdated knowledge, or inability to generalize become unreliable for real-world applications in critical domains [20,32].
- Scalability and Efficiency: Manual efforts and high computational costs limit the deployment and continuous adaptation of AI models to vast, dynamic datasets and complex environments, hindering their practical utility [3,8,44,62].
- Generalization and Adaptability: AI systems must move beyond task-specific training to effectively acquire and transfer knowledge across diverse problem settings and adapt to unforeseen changes in dynamic open worlds [24,33,37,47].
- Interpretability and Actionability: Understanding how AI systems acquire and use knowledge, and translating that into human-understandable insights, is vital for high-stakes domains like healthcare, education, and scientific discovery, bridging the “human-AI knowledge gap” [2,22,32,39,50,54].
- Robustness and Security: The KAB can expose systems to vulnerabilities, as seen in adversarial model extraction, emphasizing the need for robust knowledge safeguards and secure deployment [15].
Overcoming the KAB necessitates interdisciplinary research, moving beyond isolated solutions to foster frameworks that combine diverse knowledge representations, dynamic learning mechanisms, and enhanced human-AI collaboration. This includes developing new methodologies for data-efficient learning, enabling systems to dynamically update knowledge, bridging the gap between acquired and utilized knowledge, and improving the interpretability and explainability of AI’s internal knowledge processes.
Limitations and Future Research:
Despite significant progress, several critical limitations and unaddressed questions persist within the current understanding and tackling of the KAB. Many papers define KAB implicitly within their specific domain, limiting the generalizability and comparative analysis of solutions across disparate AI fields [52,63,64,69]. A common deficiency is the lack of quantifiable metrics for KAB’s severity beyond qualitative descriptions of cost, time, or performance drops [47]. For LLMs, understanding the theoretical underpinnings of why they struggle with knowledge extraction after continued pre-training, or why knowledge entropy decays during pre-training, remains a key challenge [68,69]. The mechanisms by which LLMs “know what knowledge is outdated” and how to effectively bridge the “cognitive gap” between LLM knowledge storage and human understanding also remain largely unexplored [12,20]. Additionally, current efforts to address KABs often introduce new complexities, such as the computational cost of Monte Carlo Tree Search (MCTS)-based methods in RAG or the ineffective knowledge utilization in LLM fine-tuning when external knowledge is injected [7,27]. Future research should focus on developing standardized KAB metrics, exploring mechanistic explanations for observed KAB phenomena (especially in black-box models), and devising integrated, generalizable frameworks that address multiple facets of the KAB concurrently, thereby fostering the development of genuinely intelligent and adaptable AI systems.
1.2 Scope and Significance of the Survey
The knowledge acquisition bottleneck (KAB), traditionally understood as the difficulty in eliciting and encoding expert knowledge into AI systems, has emerged as a pervasive and increasingly urgent challenge across various domains of artificial intelligence. The timeliness and significance of this survey are underscored by the critical role that effective knowledge acquisition plays in advancing AI capabilities, transforming AI from narrow, data-driven systems into more robust, interpretable, and adaptable intelligent agents [19,27,32,50,69,70].
The evolution of AI, particularly the proliferation of Large Language Models (LLMs) and advancements in Natural Language Processing (NLP), has paradoxically amplified the prominence and urgency of the KAB. While LLMs exhibit expansive knowledge coverage and impressive generalization capabilities [12], they introduce new facets of the KAB related to their inherent limitations, such as outdated or static knowledge, susceptibility to hallucinations, domain-specific deficits, and poor transferability across specialized tasks [5,20,27,44,70]. This necessitates continuous learning and adaptation to dynamic world knowledge, a task where LLMs frequently struggle, especially in later pretraining stages where new knowledge acquisition becomes increasingly difficult, as observed through metrics like “knowledge entropy” [69]. Furthermore, the growing reliance on AI in sensitive domains like healthcare, scientific discovery, and critical infrastructure demands interpretability, trustworthiness, and robustness, which are often hampered by the KAB [19,32,48,50,58].
Beyond developing solutions, it is crucial to both understand and rigorously measure the KAB, a perspective explicitly highlighted in the context of assessing knowledge utilization in Pretrained Language Models (PLMs) [53]. Diagnostic and analytical studies, such as those employing controlled datasets like FictionalQA to study memorization in LLMs [60], or proposing novel metrics like knowledge entropy [69], are indispensable for guiding future research. The establishment of standardized benchmarks, exemplified by Bench4KE for automated competency question generation in Knowledge Engineering (KE) [14], is fundamental for systematic evaluation and comparison of methods addressing the KAB.
This academic survey delineates the scope of research into “Attacking the Knowledge Acquisition Bottleneck” by organizing it around several main themes: frameworks, algorithms, and applications, with a critical examination of their constructive and adversarial dimensions. The inclusion of these themes is justified by their pervasive relevance across the input papers:
- Frameworks: This survey covers architectural designs and systematic approaches that streamline knowledge acquisition. Examples include
StructSense, a modular framework for structured information extraction integrating symbolic knowledge and human-in-the-loop validation [70];AutoElicit, which leverages LLMs for expert prior elicitation in predictive modeling [19];Agent KB, designed for cross-domain experience sharing in agentic problem-solving [33]; and frameworks for incremental and cumulative knowledge acquisition that aim for lifelong learning [67]. The conceptualization of a “Large Knowledge Model” that merges LLMs and KGs also represents a significant framework perspective [12]. - Algorithms: The survey analyzes specific computational methods developed to tackle the KAB. These range from
AutoPrompt, an automated method for eliciting knowledge from LLMs without fine-tuning [43], toDiversity Induced Weighted Mutual Learning (DWML)for data-efficient language model pretraining on small datasets [8]. Other algorithms focus on skill discovery in reinforcement learning (e.g.,InfoBot) [56], dynamic knowledge base construction for LLM task adaptation (e.g.,KnowMap) [44], and cost-efficient expert interaction in sensitive domains (e.g.,PU-ADKA) [4]. - Applications: The scope extends to diverse application areas where the KAB is particularly acute.
- LLMs and Natural Language Processing (NLP): This forms a major focus, encompassing information extraction (e.g., Named Entity Recognition, Relation Extraction in biomedical domain [18], scholarly articles [51]), Knowledge Graph construction and population [3,11,31,49,66], Retrieval-Augmented Generation (RAG) for improving factual accuracy and reasoning [27,63,71], continual knowledge learning and updating for ever-changing world knowledge [20,68], and intrinsically interpretable LLMs [32].
- Robotics and Game AI: In robotics, the KAB manifests in efficient skill acquisition and transfer [35,56], behavioral learning in complex systems [64], and bridging subsymbolic sensor inputs with symbolic planning [28]. For game AI, it involves human-AI knowledge transfer and discovering super-human knowledge, as demonstrated in AlphaZero [54].
- Sensitive Domains: This includes clinical NLP for patient care [21], aerospace maintenance for trusted decision support [48], education for interpretable knowledge tracing [50], and materials science for accelerated discovery [65].
- Constructive and Adversarial Dimensions: This survey examines both benevolent efforts to acquire and integrate knowledge and defensive strategies against adversarial knowledge acquisition. While most papers focus on constructive knowledge acquisition, some directly address adversarial KABs related to AI security and intellectual property protection. For instance, research on model extraction attacks (MEAs) against Machine Learning as a Service (MLaaS) platforms highlights the threat of unauthorized model acquisition and the need for defense mechanisms [15,45]. The detection of vulnerable code and intellectual property infringements through assembly clone search also represents an adversarial dimension of KAB [24]. Furthermore, the challenge of building “Trustworthy LLMs” includes mitigating risks like jailbreaks and toxic content, which involves understanding and manipulating knowledge mechanisms to prevent malicious exploitation [30].
This survey’s primary contribution is to organize the current, fragmented research landscape by systematically comparing, contrasting, and synthesizing insights from diverse approaches to the KAB. It explicitly identifies the underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations that contribute to the observed strengths, weaknesses, and performance differences between methods. For example, the convergence of neuro-symbolic AI is a recurring insight, with many works highlighting how combining LLMs’ expansive but implicit knowledge with KGs’ structured and interpretable representations can mitigate hallucinations and enhance reasoning in domains ranging from general knowledge to specialized scientific literature [12,36,66,70]. Conversely, purely fine-tuned models can often outperform LLM-based in-context learning in specific tasks, such as biomedical NER and RE, indicating a comparative weakness in generalizability for direct application [18].
Critically, the survey also assesses the limitations and potential areas for improvement or future research. Many current solutions, while effective in their specific contexts, face challenges in generalizability across domains (e.g., “quantum learning” demonstrated in pedestrian re-identification yet untested in LLMs or robotics [37]), scalability (e.g., simulating dual-decoder architectures due to GPU constraints in ontology evolution [17]), computational cost (e.g., dynamic knowledge base construction in KnowMap not fully quantified [44]), and data dependency despite efforts toward data efficiency [43,57]. Furthermore, ethical considerations, bias mitigation, and the trade-offs between model size and knowledge integration capabilities remain largely unaddressed in many specialized studies [69]. By pinpointing these limitations and unaddressed questions, the survey aims to highlight future research directions that are crucial for developing more robust, efficient, and ethical AI systems. The subsequent sections will delve into specific solutions within these themes, examining their technical details, empirical impact, and implications for a more comprehensive understanding of how to effectively attack the KAB.
2. Characterizing the Knowledge Acquisition Bottleneck
The Knowledge Acquisition Bottleneck (KAB) represents a fundamental and pervasive challenge across diverse fields of artificial intelligence, broadly defined as the inherent difficulty, cost, and inefficiency associated with collecting, representing, structuring, updating, and effectively utilizing knowledge within AI systems [3,44,52]. This bottleneck prevents AI systems from efficiently acquiring and leveraging the necessary information to operate adaptively, intelligently, and reliably in complex, real-world, and dynamic environments. It is not a monolithic problem but rather a multi-dimensional constraint space impeding AI’s cognitive capabilities.
To systematically characterize the KAB, we propose a theoretical framework that delineates its manifestations and underlying causes across four primary dimensions:
- Resource Constraints: This dimension encompasses the tangible limitations on knowledge acquisition, primarily driven by the extensive manual effort and high economic costs [19,21,41]. It includes the labor-intensive processes of data labeling, annotation, expert elicitation, and the significant computational costs associated with training and maintaining complex AI models, especially Large Language Models (LLMs) [44,64]. The scarcity of high-quality labeled data further exacerbates this constraint, hindering model training and generalization [3,25].
- Cognitive Constraints: This dimension refers to the limitations in AI models’ inherent abilities to process, represent, or reason with knowledge due to architectural designs or the complexity of the knowledge itself. Key issues include architectural mismatch between textual and structured representations, preventing effective integration of knowledge graphs with LLMs [12,42]. The opacity of AI systems, particularly LLMs, leads to interpretability bottlenecks, making it challenging to understand how knowledge is used or to generate human-level explanations [32,50]. Furthermore, a significant human-AI knowledge gap emerges when AI systems develop reasoning principles and concepts not readily understandable or leveraged by human experts [37,54].
- Dynamic Constraints: This dimension highlights the challenges associated with maintaining and adapting knowledge in evolving environments. A critical problem, especially for LLMs, is their reliance on static, pre-trained knowledge, leading to
outdated information,hallucinations, andknowledge forgettingwhen confronted with new data [5,44]. Catastrophic forgetting, where previously acquired knowledge is lost upon learning new tasks, is a pervasive issue, often linked to the decay ofknowledge entropyduring pre-training, which reduces the model’s plasticity for new knowledge acquisition [69]. - Epistemic Constraints: This dimension focuses on issues related to the quality, certainty, and generalizability of knowledge. Knowledge acquisition is frequently bottlenecked by environments characterized by inherent uncertainty, partial observability, and difficulties in generalizing knowledge beyond specific training distributions [37]. Data quality issues, such as annotation inconsistencies or incompleteness in structured knowledge bases, also lead to
knowledge incompletenessanddata sparsity, impacting system reliability and performance [25,55].
These KAB dimensions are often rooted in labor-intensive processes for knowledge engineering and annotation, which severely limit scalability and continuous updates [3]. Within LLMs, internal dynamics characterized by “knowledge circuits” and “knowledge entropy decay” underpin their ability, or inability, to integrate and retain information efficiently [34,69]. Furthermore, the “acquired knowledge gap” (what models know) and the “knowledge utilization gap” (how much of that knowledge they can effectively use) in pre-trained language models highlight critical limitations in current evaluation methodologies [53].
The manifestations of the KAB vary significantly across specific AI domains. For LLMs, this includes issues like insufficient knowledge utilization and hallucinations due to outdated or conflicting information [44,53]. Knowledge Graphs grapple with the manual effort for construction and the challenges of data heterogeneity and incompleteness [3]. In Natural Language Processing (NLP), particularly clinical applications, data scarcity and the high cost of human annotation are prevalent [21]. In MLaaS security, the KAB is framed by adversarial query costs and intellectual property concerns related to model extraction [15]. Binary code analysis struggles with the invariance to compilation nuisances and poor generalization to out-of-domain architectures [24]. Robotics and Reinforcement Learning face data scarcity, the reality gap, and the curse_of_dimensionality [64].
Across all these domains, persistent cross-cutting challenges include architectural mismatch, scalability limitations, data scarcity, issues of reliability and interpretability, and the difficulty of achieving Out-of-Distribution (OOD) generalization. Addressing these multifaceted challenges requires moving beyond incremental improvements toward developing novel frameworks and algorithms that prioritize efficiency, scalability, robustness, and interpretability in knowledge acquisition and utilization. Future research must focus on developing standardized, quantifiable metrics for KAB severity to enable robust comparative analyses and to provide clearer targets for mitigation efforts, ultimately aiming to bridge the critical human-AI knowledge gap [12,30].
2.1 Definition and Manifestations
The Knowledge Acquisition Bottleneck (KAB) represents a pervasive challenge across diverse fields of artificial intelligence, broadly defined as the inherent difficulty, cost, and inefficiency associated with collecting, representing, structuring, updating, and effectively utilizing knowledge within AI systems. This encompasses the fundamental obstacles preventing AI from efficiently acquiring and leveraging the necessary information to operate adaptively, intelligently, and reliably in real-world, dynamic environments [3,44,52].
The manifestations of KAB can be categorized into several distinct types, reflecting the multifaceted nature of knowledge acquisition:
1. Manual Effort and Economic Costs: A dominant manifestation of the KAB stems from the extensive manual effort and high economic costs required for knowledge engineering. This includes the labor-intensive process of data labeling and annotation, which is often expensive, time-consuming, and prone to errors [3,6,10,14,16,18,19,21,25,31,41,51,57,72,75]. For instance, populating leaderboards for machine learning research requires “laborious and error-prone” human annotation of results [41], and creating high-quality sense-annotated corpora for Word Sense Disambiguation (WSD) is “laborious and expensive” [10]. Similarly, in the clinical NLP domain, manual chart review for extracting medical events is “prohibitively expensive” [21]. The elicitation of well-specified prior distributions from human experts for predictive models is also a “challenging, costly, or infeasible” endeavor, especially in low-resource settings [19]. For Large Language Models (LLMs), prompt engineering demands “heavy dependence on manual expertise” [43,44]. The high costs extend to physical robot maintenance, which limits the number of training episodes and necessitates constant human oversight during learning, contributing to resource constraints [64]. In adversarial model extraction, the cost of model extraction queries, billed pro rata, imposes strict budget constraints, compelling adversaries to minimize API calls [15,45].
2. Data Scarcity and Quality Issues:
A prevalent bottleneck is the scarcity of sufficiently large and high-quality labeled data, hindering model training and generalization. This data scarcity is noted across various domains: for large-scale labeled data requirements in supervised fine-tuning (SFT) of LLMs [44], for new resources in Knowledge Graph (KG) construction [74], for full-text scientific articles and novel facets in scholarly information extraction [51], and for low-frequency knowledge in LLMs due to insufficient representations [34]. Robotics faces data scarcity due to physical constraints, wear-and-tear, and high maintenance costs [64]. Clinical NLP for rare events like hypoglycemia also struggles with data scarcity for training robust models [21].
Beyond mere quantity, data quality is critical. Issues like manual annotation inconsistencies or errors lead to lower quality training data and significant performance drops; for instance, models trained on single-annotated data for Named Entity Recognition (NER) show a 9.8% F-score drop compared to double-annotated data [25]. The vast majority of experimental data in scientific domains remains “locked in semi-structured formats” like tables and figures, creating a computational challenge for knowledge extraction [65]. Even large KBs can be “error-prone and have lot many facts that are still missing” [9], highlighting knowledge incompleteness and data sparsity in structured forms.
3. Modeling Complexity and Architectural Mismatch:
This type of KAB arises when current AI models struggle to process, represent, or reason with knowledge due to limitations in their design or the inherent complexity of the knowledge itself. The “modeling bottleneck” is evident in classical planning, where autonomously acquiring classical planning models from subsymbolic inputs faces the “Symbol Stability Problem” (SSP). This issue, caused by systemic and statistical uncertainties, results in unstable latent representations that degrade search performance, disconnect the search space, and complicate hyperparameter tuning [28]. Similarly, in Knowledge Tracing (KT), traditional methods use “opaque latent embeddings” lacking interpretability, while LLM-based explanations can “hallucinate,” compromising reliability and preventing actionable insights for educators [50].
LLMs, despite their capacity, frequently struggle with structured relational knowledge, leading to suboptimal results on knowledge-intensive tasks [12,42]. They often fail to “fully exploit relational patterns” for complex or multi-hop reasoning, contributing to factual errors and hallucinations [30,71]. This architectural mismatch is also evident in integrating structured KGs with free-form text [1] and in LLMs’ inability to adequately process granular external knowledge, often treating it “as functionally equivalent to random noise” [7]. The difficulty in handling highly flexible domain-specific terminology (e.g., in clinical notes or operations and maintenance records) further exemplifies this modeling challenge, as manually specifying rules becomes impossible [21,48]. Agentic systems also face architectural issues like “Task-Specific Experience Isolation” and “Single-Level Retrieval Granularity,” preventing knowledge transfer and efficient adaptation across tasks [33].
4. Dynamic Knowledge Maintenance and Forgetting:
A critical challenge, particularly for LLMs, is their reliance on “static, pre-trained knowledge” that becomes “outdated or insufficient when confronting evolving real-world challenges” [5,20,30,44,68]. This leads to hallucinations and unreliable performance [5]. LLMs struggle to “dynamically update and extract newly acquired factual information” even after continued pre-training, exhibiting “impaired question-answering (QA) capability” and “constrained knowledge retrieval” [68].
Knowledge forgetting is a significant sub-category. Catastrophic forgetting occurs when models lose previously acquired knowledge upon learning new tasks, a pervasive issue in continual learning [5,26,44,67]. This is quantitatively measured by knowledge entropy decay during pre-training, where LLMs show a consistent decline in the range of memory sources utilized, leading to reduced ability to acquire new knowledge and increased forgetting rates in continual learning scenarios [69]. For instance, a strong Pearson correlation of 0.94 between knowledge entropy and acquisition, and -0.96 with forgetting, highlights this phenomenon [69]. This issue is exacerbated by LLMs’ lack of an inherent mechanism to memorize newly retrieved information, necessitating repeated retrieval for future use [27]. In robotics, dynamic robot properties like wear and temperature changes make learned behaviors quickly outdated, demanding dynamic knowledge maintenance [64].
5. Interpretability and Representation Bottlenecks:
This KAB arises from the opacity of AI systems’ internal workings, preventing understanding of how knowledge is used. In knowledge tracing, interpretability is crucial as predictive accuracy alone can be misleading [50]. LLMs, despite their knowledge, struggle with self-awareness and human-level explanations, lacking “semantically interpretable knowledge resources” crucial for action justification [58]. This lack of introspectability makes it difficult to ensure reliability, detect misuse, and debug flawed reasoning [32,36]. In scientific domains, highly accurate ML predictions from satellite imagery often fail to yield “scientific insight” or new knowledge because the models cannot explain why predictions are made, hindering understanding of causal relationships for social scientists and policymakers [39].
6. Human-AI Knowledge Gap:
A distinct KAB emerges when AI systems, particularly those achieving superhuman performance through self-play (e.g., AlphaZero), develop reasoning principles and concepts that are not derived from or constrained by human knowledge. This “human-AI knowledge gap” ($M-H$ set) represents machine-specific knowledge ($M$) not yet part of human understanding ($H$) [54]. Such a gap is evident when AI decisions are initially incomprehensible to human experts but are later validated as superior, limiting human experts’ ability to leverage AI insights [54]. This gap is also observed when LLMs struggle with polysemous terms and domain-specific terminology, requiring ontological grounding to prevent hallucinations and ensure correct interpretation [70]. Furthermore, the lack of universal measurement standards across diverse feature distributions can lead to AI misidentifying objects, as it hasn’t learned the “differences in feature distributions between knowledge systems” [37].
7. Scalability and Computational Limitations:
The sheer volume of data and the computational demands of modern AI systems pose significant KABs. The “explosion in the number of machine learning publications” makes manual tracking of state-of-the-art “unsustainable over time” [11,41]. In KG construction, manual approaches are not scalable for continuous updates from large, diverse data sources, leading to inefficient learning paradigms and high re-computation costs [3,49]. LLMs face significant computational and memory requirements, along with massive data demands for training, which complicate deployment on edge systems [8]. High computational costs for Reinforcement Learning (RL) and lengthy training processes for SFT are also noted [44]. In robotics, the “curse of dimensionality” poses scalability issues for high-DOF robots, and real-time execution limits learning speed [64].
8. Uncertainty and Generalization Issues:
Knowledge acquisition is bottlenecked by environments characterized by uncertainty, partial observability, and difficulties in generalizing knowledge. In open-world settings, significant differences in data distribution and feature representation lead to poor generalization for models trained on one domain and applied to another [37]. This is further complicated by “insufficient confidence in new knowledge” and challenges in incremental recognition with infinite label spaces [37]. RL systems face KABs from “sparse rewards, partial observability, and vast state spaces,” making efficient exploration difficult and resulting in a “vanishing probability of reaching the goal randomly” [35,56]. Knowledge is also bottlenecked by its “invariance” to skill, data distribution (Out-of-Distribution generalization), and data syntax, where models fail to adapt knowledge across varying contexts [47]. Within KG construction, uncertainty management is a major KAB, as KGs suffer from “knowledge deltas” arising from invalidity, vagueness, fuzziness, timeliness, ambiguity, and incompleteness, which impact KG quality and downstream applications [55].
Acquired Knowledge Gap vs. Utilized Knowledge Gap in PLMs:
| Aspect | Acquired Knowledge Gap | Utilized Knowledge Gap | Implication for KAB |
|---|---|---|---|
| Definition | Missing facts in the model’s parametric knowledge. | Inability to effectively apply already acquired knowledge in downstream tasks. | Model knows but cannot use its knowledge effectively. |
| Quantifies | What the model knows. | How much of that knowledge can be effectively used. | Reveals a disconnect between presence and applicability. |
| Measurement Example | Top-1 accuracy on diagnostic fact-checking datasets. | Performance drop on tasks designed from the model’s known facts. | Traditional metrics may overestimate true capability. |
| Manifestation | Model lacks specific factual information. | Knowledge is present but deployment is ineffective, inflexible, or sub-optimal. | Even with knowledge, system is unreliable or inefficient. |
| Observed in PLMs | Larger models acquire more facts. | Persists even with larger models, suggesting internal limitations (e.g., inductive biases). | Scaling alone is insufficient to close the utilization gap. |
| Contribution to Hallucination | Model invents missing facts due to lack of knowledge. | Model fails to apply correct knowledge, leading to incorrect generation despite internal presence. | Both contribute to unreliability and factual errors. |
Pre-trained Language Models (PLMs) exhibit a crucial distinction in their KAB: the “acquired knowledge gap” and the “knowledge utilization gap” [53]. The acquired knowledge gap refers to the missing facts in the model’s parametric knowledge, quantifying what the model knows (e.g., top-1 accuracy on diagnostic fact-checking datasets) [53]. In contrast, the knowledge utilization gap signifies how much of the already acquired parametric knowledge can be effectively utilized in downstream tasks. This gap manifests as a significant performance drop on tasks specifically designed from the model’s known facts, suggesting insufficient knowledge utilization even when knowledge is present internally [53]. For instance, a model like RoBERTa might acquire more facts than GPT-Neo but achieve similar downstream performance due to a larger utilization gap, implying an inability to apply stored knowledge effectively to relevant tasks [53]. This distinction is robust across different knowledge base sizes and negative sampling strategies, indicating inductive biases within the model or fine-tuning process as potential culprits [53]. This problem is further compounded by “knowledge conflicts,” where LLMs might favor internally memorized (potentially outdated) knowledge over explicitly provided, correct external context, creating a “knowledge acquisition-utilization gap” where external information is available but not effectively applied [20,36,44].
Knowledge Forgetting and LLMs’ Dynamic Knowledge Challenges:
Knowledge forgetting in AI systems, particularly LLMs, is defined as the degradation or loss of previously learned information upon continuous learning or exposure to new data. Beyond catastrophic forgetting, recent studies have introduced quantitative measures. One such measure is knowledge entropy, a metric derived from the feed-forward networks (FFNs) of LLMs, which quantifies the range of memory sources a model utilizes. A decline in knowledge entropy during pre-training, consistently observed in models like OLMo and Pythia, suggests that models increasingly rely on a narrower set of active memory vectors, leading to reduced ability to acquire new knowledge and increased rates of forgetting in continual learning scenarios [69].
These internal dynamics profoundly impact LLMs’ ability to continuously update and integrate dynamic world knowledge. LLMs are characterized by their static nature post-training, making rapid adaptation to novel tasks in dynamic environments challenging [44,68]. They struggle to extract newly acquired factual information, even after continuous pre-training on new corpora, leading to impaired QA performance and constrained knowledge retrieval [68]. This manifests as initial closed-book evaluations showing “extremely low performance” (e.g., 2% Exact Match) for new knowledge, indicating LLMs possess virtually none of the target domain’s new facts [68]. The “abnormal learning behavior” of LLMs, where fine-tuning for QA tasks can lead to forgetting original biographical text, underscores the fragility of parametric knowledge and the complex interplay between different knowledge representations [73]. The challenge lies in how LLMs internalize new information and structurally integrate it, with acquisition efficiency being influenced by the relevance and frequency of new knowledge to pre-existing knowledge [34].
Communalities, Nuances, and Critical Assessment:
Across these diverse manifestations, a common thread is the significant economic and practical burden they impose. This includes substantial labor costs, prolonged development times, diminished system reliability, and underutilized AI capabilities. The sheer scale of data in modern systems leads to scalability challenges, whether in tracking scientific literature (e.g., over 33,000 ML papers in 2019, growing 50% yearly [41]) or managing petabytes of operational data.
However, each domain presents specific nuances:
- LLMs: The KAB is deeply intertwined with their parametric knowledge storage, statistical learning capabilities, and the inherent trade-off between broad generalization and deep domain-specific expertise. Their susceptibility to
hallucination,knowledge conflicts,limited context windows, andknowledge forgettingare architectural shortcomings [12,30,36]. The critique for LLMs often centers on the difficulty in quantifying the “cognitive gap” or the exact severity of knowledge fragility [12,30]. - Knowledge Graphs: The core KABs are related to
incompleteness,data heterogeneityfrom diverse sources,error propagationin construction pipelines, and the constant need for dynamic maintenance and quality control from potentially noisy facts [3,23,55]. The theoretical foundation often involves symbolic representation and formal logic, which contrasts with the statistical nature of LLMs. - Robotics: KABs are significantly influenced by physical constraints, high costs of real-world interaction, the
reality gapbetween simulation and reality, and the need to cope with partial observability and uncertainty in unstructured environments [64]. This often highlights the challenges of grounding abstract knowledge in embodied agents. - Model Extraction: The KAB is defined by an adversarial context, where the “adversary lacks access to the secret training dataset” and faces severe query budget constraints [15,45]. This necessitates active learning strategies to optimally select samples for querying.
- Knowledge Tracing: The primary bottleneck is the
interpretabilityof student knowledge states, moving beyond opaque latent embeddings to actionable insights for human educators [50].
Critically, many analyses, while effectively identifying KABs, often lack a broad theoretical exploration beyond their specific domain, or quantitative measures of the bottleneck’s severity in terms of universal costs, time, or performance impacts before applying their proposed solutions [5,6,10,11,12,14,16,19,21,23,25,28,29,30,37,39,40,41,42,44,48,51,57,59,62,64,65,67,68,71,74]. Future research should focus on developing standardized, quantifiable metrics for KAB severity to enable more robust comparative analyses across AI paradigms and to provide clearer targets for mitigation efforts. The challenge of how to effectively bridge the human-AI knowledge gap, instill true logical reasoning in LLMs, and efficiently integrate dynamic, multi-modal knowledge remains an open and critical area for investigation.
2.2 Underlying Causes and Limitations of Traditional Approaches
The Knowledge Acquisition Bottleneck (KAB) poses a persistent challenge across diverse domains of artificial intelligence, rooted in fundamental limitations of traditional methodologies and emerging issues within modern paradigms like Large Language Models (LLMs). These limitations stem from inherent assumptions, architectural choices, and domain-specific adaptations that collectively impede the efficient, scalable, and reliable acquisition, representation, and utilization of knowledge.
A primary and pervasive root cause of the KAB lies in the labor-intensive processes that necessitate extensive human domain expertise, impose significant cognitive load, and make formalizing complex knowledge exceedingly difficult. This bottleneck manifests acutely in several areas:
- Manual Knowledge Engineering and Annotation: Constructing Knowledge Graphs (KGs) traditionally demands substantial manual intervention for identifying relevant sources, defining ontologies, mapping data, and validating quality [3]. This manual effort is costly, time-consuming, and resource-intensive, requiring specialized domain experts [3,4,6,10,12,14,17,19,25,28,29,36,55,63,72]. For instance, rule-based systems in information extraction (IE) are difficult to scale due to the impossibility of manually specifying rules for all patterns in flexible language, such as clinical notes [9,21]. High-quality prompt engineering for LLMs similarly introduces a time-consuming and laborious manual effort, akin to traditional knowledge engineering [12,43].
- Scalability Issues: The inherent labor-intensiveness of manual annotation and rule definition severely limits scalability, making these approaches impractical for large volumes of data or rapidly evolving knowledge domains [3,8,10,11,12,21,23,31,32,38,41,51,55,59,63,65,66,67,75]. This is particularly problematic for ontology evolution, which struggles to keep pace with the growth of unstructured information [17].
Within LLMs, two theoretical perspectives shed light on the internal dynamics governing knowledge integration and loss. The concept of “knowledge circuits” proposes that knowledge acquisition within LLMs is driven by “topological changes” and the cooperative interplay between multiple components like attention heads and MLPs, rather than isolated knowledge blocks [34]. This theoretical foundation suggests a complex, distributed representation of knowledge. Conversely, the empirical observation of “knowledge entropy decay” during language model pretraining reveals that as training progresses, the distribution of memory coefficients in Feed-Forward Network (FFN) layers becomes sparser, leading to reliance on a limited set of memory vectors [69]. This reduced plasticity makes efficient new knowledge acquisition difficult and increases the risk of catastrophic forgetting, where new information overwrites existing, frequently used knowledge [5,20,26,36,67]. A consolidated view suggests that while LLMs form intricate “knowledge circuits” through topological changes to encode information, the continuous decay of “knowledge entropy” limits the dynamic range and plasticity of these circuits. This makes it challenging to form new, stable circuits for novel knowledge or to efficiently update existing ones without destabilizing previously learned information, thus contributing to the KAB in LLMs.
Prior methodological limitations in evaluating knowledge utilization have often obscured the true nature and persistence of the KAB in pre-trained language models (PLMs). Confounding factors, such as “shortcuts or insufficient signal” from “arbitrary crowd-sourced tasks” and the use of synthetic datasets that are not comprehensive or dynamic enough, have led to misleading assessments of knowledge acquisition and utilization [20,43,53,60,73]. This results in a “knowledge acquisition-utilization gap,” where models possess knowledge internally but fail to effectively leverage it for downstream tasks or novel scenarios [7,27,42,49,68].
Theoretical explanations for the KAB vary significantly across different AI paradigms:
- Reinforcement Learning (RL): KAB in RL is attributed to challenges such as sparse rewards, vast state spaces, partial observability, and the inherent difficulty of exploration and policy generalization [56]. Traditional exploration methods often lack the ability to leverage experience from previous tasks, preventing efficient knowledge transfer and adaptation to new environments [56].
- Educational AI: Knowledge representation in educational AI faces interpretability and reliability issues. Traditional Knowledge Tracing (KT) methods represent student knowledge as “opaque, high-dimensional latent vectors,” hindering actionable insights for educators [50]. Newer LLM-based approaches, while promising, risk “hallucination” and lack accuracy guarantees, compromising their reliability for educational tools [2,50]. Traditional methods also struggle with non-personalization, predefined concepts, static knowledge assumptions, and difficulty modeling non-graded learning materials, leading to data scarcity for explicit knowledge gain signals [22].
- Deep Learning (DL): A major limitation is its pervasive reliance on large volumes of meticulously annotated examples [16]. This “extreme data-dependence” leads to scalability issues for manual annotation, making data acquisition both time-consuming and expensive [8,25,57]. Weak supervision methods often produce incorrect or inconsistent labels, and joint inference involves significant modeling complexity and computational intractability [16].
- Full Text Processing: In scholarly information extraction, traditional approaches often relied on partial text (e.g., abstracts), missing crucial details only present in full texts [51]. Existing neural models also faced data scarcity and architectural mismatch for comprehensive full-text processing, struggling with document-level context and long-range relations [11,51].
- Competency Question Generation: The KAB here is characterized by the labor-intensive manual formalization of competency questions and their validation, coupled with a lack of standardized evaluation benchmarks and reusable datasets, constituting a significant methodological flaw [14].
KAB Root Causes and Limitations by AI Paradigm
| AI Domain / Area | Primary Root Causes of KAB | Limitations of Traditional Approaches (Pre-LLM) | Emergent LLM Limitations (if applicable) |
|---|---|---|---|
| General Knowledge Engineering | Labor-intensive manual processes, High human expertise dependency, Cognitive load for formalization | Costly, Time-consuming, Resource-intensive, Not scalable for evolving knowledge | Manual prompt engineering, Sensitivity to phrasing |
| Knowledge Graphs (KGs) | Manual schema definition/population, Data heterogeneity, Error propagation in pipelines | Scalability issues for continuous updates, Lack of comprehensive entity fusion/quality assurance | Hallucination, Reliability issues for generative KGC |
| Reinforcement Learning (RL) | Sparse rewards, Vast state spaces, Partial observability, Difficulty of exploration/policy generalization | Inability to leverage experience from previous tasks (transfer learning) | - |
| Educational AI | Opaque knowledge representation, Difficulty modeling non-graded learning, Student selection bias | Limited interpretability of student knowledge states (latent vectors), Static knowledge assumptions | Hallucination in LLM explanations, Lack of accuracy guarantees |
| Deep Learning (DL) | Extreme data dependence, Need for meticulous annotation | Scalability issues for manual annotation, Noisy/inconsistent labels from weak supervision | Computational cost, Data dependency on massive datasets |
| Full Text Processing (e.g., Scientific) | Manual tracking of state-of-the-art, Extracting complex technical facets | Reliance on partial text (e.g., abstracts), Architectural mismatch for document-level context | - |
| Competency Question Generation | Labor-intensive manual formalization/validation, Lack of standardized evaluation/reusable datasets | Methodological flaws (e.g., lack of benchmarks) | - |
| Traditional Robotics | Accurate modeling of complex real-world dynamics, Hand-crafted solutions are brittle | Knowledge/Engineering/Tractability/Precision bottlenecks, Intractability of modeling soft bodies/fluids | - |
| AlphaZero (Game AI) | - | Human biases, Reliance on heuristics, Limited computational capacity (in humans) | Human-AI knowledge gap ($M-H$ set) - machine knowledge incomprehensible to humans |
| Binary Code Analysis | Compilation artifacts (function inlining, injected code), Sensitivity to compiler variations | Poor OOD generalization, Over-reliance on task-specific data, Learning “nuisance information” | Architectural mismatch for semantic understanding |
| Pre-trained Language Models (PLMs) | Knowledge circuits/entropy decay, Acquired/Utilized knowledge gap | Confounding factors in evaluation (shortcuts, insufficient signal), Synthetic datasets not dynamic enough | Catastrophic forgetting, Ineffective knowledge utilization, Hallucational reasoning, Lack of transparent reasoning |
Critically comparing root causes across different AI domains reveals distinct yet interconnected limitations:
- Traditional Robotics vs. ML: Traditional robotics, with its reliance on explicit models, encounters severe “knowledge,” “engineering,” “tractability,” and “precision” bottlenecks [64]. Accurately modeling complex real-world dynamics (e.g., soft bodies, fluids) is often intractable, and hand-crafted solutions become brittle in changing environments [64]. This contrasts sharply with machine learning’s ability to directly learn from experience and adapt to unmodeled dynamics, though sometimes at the cost of interpretability or requiring vast amounts of data [64].
- AlphaZero’s Self-Taught Capability vs. Human Bias: AlphaZero’s ability to learn strategies solely through self-play, unconstrained by human supervision, led to the discovery of “unconventional” and “unorthodox” knowledge ($M-H$ set) that human experts might overlook due to their inherent biases, reliance on heuristics, and limited computational capacity [54]. This highlights a fundamental “human-AI knowledge gap,” where human analysis can inadvertently limit the discovery of truly novel AI concepts by attempting to “shoehorn” machine knowledge into existing human frameworks [54].
- Classical Model Extraction vs. Assembly Code Analysis: Classical model extraction often necessitates a “domain knowledge requirement,” demanding access to subsets of secret datasets or hand-crafted examples, posing a significant “human expertise dependency” for an adversary [15]. In contrast, traditional learning-based approaches for assembly code analysis suffer from a lack of “human expert knowledge” integration and an over-reliance on task-specific data. This leads to severe Out-of-Distribution (OOD) generalization failures and sensitivity to compiler variations, making models inapplicable to unseen architectures and toolchains [24]. Existing models inadvertently learn “nuisance information” from training data, further hindering their transferability [24].
Across these varied applications, several cross-cutting limitations emerge. Architectural mismatch is a recurring theme, hindering the seamless integration of structured and unstructured data, preventing models from leveraging crucial structural information (e.g., in KGs), or leading to suboptimal knowledge transfer mechanisms [1,3,4,8,12,13,16,18,21,26,27,28,31,32,33,37,42,46,58,62,63,67,70,74]. This is evident in the difficulty of blending structured data with free-form text or the challenges of adapting RAG pipelines, primarily designed for unstructured text, to structured graph data [1,63]. The architectural constraints of LLMs also mean they lack substantial pre-training on graph-structured data, impairing their inherent performance on graph-related tasks [63].
Scalability and computational costs remain significant hurdles, from the batch-oriented processing of traditional KG construction leading to redundant computation [3], to the prohibitive costs of retraining massive LLMs or performing extensive human annotation [20,27,44]. Even modern methods like LLM-based interpretable models face scalability issues due to numerous costly API queries [32]. Data scarcity and dependency are equally critical, as many advanced models still require vast amounts of accurately labeled data, which is difficult and expensive to obtain, especially in domain-specific or low-resource settings [16,21,25,48,57,70].
Furthermore, the phenomena of hallucination, lack of reliability, and poor interpretability are significant limitations, particularly concerning LLMs. LLMs frequently generate texts that lack factual accuracy or contextual relevance [2,5,12,17,29,30,36,55,59,66,70]. This arises from issues such as improper learning data distribution, internal memory conflicts, and a lack of mechanisms for “mover heads” within LLMs [30]. The absence of provenance or reliability information further compromises the utility of LLM-extracted knowledge, particularly in sensitive domains [55]. Finally, OOD generalization remains a critical challenge, as models tend to overfit to specific domains, learn spurious correlations, and struggle to transfer knowledge effectively to new, unseen environments [24,27,37,42,48,70,72].
These limitations underscore the pressing need for novel frameworks and algorithms that can overcome the KAB by balancing efficiency, scalability, robustness, and reliability across the diverse landscape of AI applications. Addressing these underlying causes will require moving beyond mere incremental improvements to rethinking fundamental architectural designs, knowledge representation schemes, and evaluation methodologies.
2.3 Manifestations in Specific Domains
The Knowledge Acquisition Bottleneck (KAB) is a pervasive challenge across diverse fields of artificial intelligence, manifesting uniquely in each domain due to distinct underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations. A comparative analysis reveals that while some challenges like data scarcity and the need for human expertise are widespread, their precise nature, severity, and optimal mitigation strategies vary significantly. This section provides a high-level overview of KAB manifestations across key AI domains, setting the stage for more detailed discussions in subsequent subsections.
In the realm of Large Language Models (LLMs), the KAB is multifaceted, primarily stemming from their reliance on massive, static pre-training corpora. Key manifestations include insufficient knowledge utilization and a persistent knowledge acquisition-utilization gap where LLMs possess encyclopedic facts but struggle to reliably apply or retrieve them in downstream tasks or novel contexts [27,53,61,68,73]. The static nature of their training data leads to outdated knowledge, hallucinations, and knowledge forgetting during continual learning or updates, where new information overwrites prior memorization [5,20,30,34,69]. Furthermore, LLMs exhibit a lack of deep domain-specific knowledge [2,4,44] and struggle with the integration and utilization of structured knowledge like that found in Knowledge Graphs (KGs), often yielding sub-optimal results and hallucinations due to architectural mismatch between textual and structured representations [1,12,17,36,42,63]. Interpretability and controllable generation remain significant challenges, particularly given the opacity of their internal decision-making processes [32,59].
In Knowledge Graphs (KGs) and Knowledge Engineering, the KAB is primarily rooted in the manual effort and human expertise required for their construction, curation, and continuous management [3,9,12,14,31,55,66]. Challenges include data heterogeneity from diverse sources, scalability issues in processing vast and dynamic information, incompleteness of real-world knowledge, and stringent quality control measures to maintain accuracy and consistency [3,11,23,31,38,40,55]. This contrasts sharply with LLMs, where the challenge is less about creating structured knowledge from scratch and more about effectively utilizing existing knowledge.
For Natural Language Processing (NLP), particularly in specialized domains like Clinical NLP, data scarcity and the high cost of human annotation are central KAB manifestations [9,16,18,19,21,25,57,72]. This is exacerbated by specialized vocabularies, inconsistent structures, rare entities, and small record sizes in fields like aviation and maintenance, leading to domain-specific knowledge gaps and poor performance of generic NLP tools [6,48,70]. In scholarly information extraction, the KAB is driven by the exponential growth of scientific literature, leading to information overload and the manual effort required to track state-of-the-art and extract complex technical facets [41,51]. Word Sense Disambiguation (WSD) similarly struggles with data scarcity for sense-annotated corpora and the noise introduced by automatically generated resources [10].
In MLaaS Security and Binary Code Analysis, the KAB is characterized by adversarial constraints and the inherent obfuscation of information. For Adversarial Model Extraction (AME) in MLaaS, the bottleneck is defined by the adversary’s lack of secret training data and the need to minimize costly queries to the proprietary service, highlighting a knowledge challenge centered on query costs and intellectual property concerns [15,45]. This presents a different manifestation than the manual model specification in classical planning. In Binary Code Analysis, the KAB stems from the profound difficulty in achieving generalizable semantic understanding due to compilation artifacts. Models struggle with data scarcity for unseen compiler variants, function inlining, and compiler-specific injected code, leading to architectural mismatch and poor generalization to out-of-domain architectures and libraries [24].
Within Robotics and Reinforcement Learning (RL), the KAB manifests as a range of challenges, including data scarcity in real-world environments, the reality gap between simulation and physical systems, and the curse of dimensionality in vast state-action spaces [35,56,64]. Other issues include uncertainty in dynamic environments, modeling complexity for deformable objects or dynamic manipulation, and safety risks associated with learning in physical systems. Interpretability of learned skills also poses a challenge [35]. This “reality gap” in robotics contrasts with the “M-H gap” in game AI, where the challenge is understanding and transferring machine-unique concepts rather than bridging physical simulation differences [54,64].
For Classical Planning and Game AI, the KAB focuses on symbolic representation and human-AI knowledge alignment. In classical planning, the KAB is primarily the manual symbolic model specification and the symbol grounding problem from raw, subsymbolic data, exacerbated by the lack of labeled action data [28,29]. This differs significantly from the difficulty in understanding internal knowledge states in knowledge tracing, which deals with student learning models [50]. In Game AI, especially with agents like AlphaZero, the KAB appears as machine-unique concepts and a human-AI discrepancy in how knowledge is interpreted and applied, making super-human strategies difficult for humans to extract and learn from [54].
In Educational Technologies and Knowledge Tracing (KT), the KAB centers on interpretability and the comprehensive modeling of student learning. Traditional KT models often rely on opaque latent embeddings that provide limited interpretability for teachers and learners, failing to offer actionable insights into knowledge gaps or misconceptions [50]. Furthermore, these models often assume quasi-static knowledge states and struggle to integrate knowledge acquired from multiple, heterogeneous learning resource types, leading to an incomplete understanding of student proficiency [22].
Beyond these major categories, KABs manifest in various other specialized domains. In Computer Vision, beyond general object recognition, manifestations include the inability to incorporate higher-level conceptual information (e.g., functionality, intentionality) and commonsense knowledge for tasks like event and scene recognition [72]. The poverty and welfare domain demonstrates a KAB not in data acquisition, but in the failure of ML models to generate scientific insights and causal understanding from satellite imagery, limiting actionable knowledge for policymakers [39]. Materials science faces challenges with data heterogeneity in semi-structured formats within scientific tables, hindering large-scale analysis of composition-property relationships [65]. Cross-domain general AI and cognitive systems face a KAB in their inability to adapt and transfer knowledge effectively across different tasks, data distributions, and syntaxes, often falling prey to spurious correlations and struggling with non-Euclidean data types [26,47].
Across these diverse manifestations, several common underlying challenges emerge: the persistent need for robust and efficient mechanisms to acquire, integrate, and dynamically update knowledge; the struggle for models to generalize beyond their training distribution or specific task formulations; the imperative for greater interpretability and explainability, particularly in sensitive domains; and the ongoing challenge of effectively bridging symbolic and sub-symbolic knowledge representations. Addressing these requires a deeper understanding of the inherent complexities within each domain, the development of architectures that can disentangle salient information from noise, and innovative frameworks for managing knowledge throughout its lifecycle.
2.3.1 Adversarial Model Extraction and MLaaS Security
Adversarial Model Extraction (AME) poses a significant challenge within the realm of Machine Learning as a Service (MLaaS) security, representing a critical knowledge acquisition bottleneck (KAB) for both adversaries and service providers. At its core, AME involves an attacker attempting to replicate a proprietary MLaaS model by strategically querying the service, thereby reconstructing a high-fidelity local replica [45]. This KAB is characterized by distinct constraints and objectives that differentiate it from other knowledge acquisition challenges, such as data scarcity in knowledge graphs (KGs) or high annotation costs in clinical Natural Language Processing (NLP) [15].
Adversarial Model Extraction KAB: Adversary vs. Provider Perspectives
| Aspect | Adversary’s KAB Challenges & Objectives | Provider’s KAB Challenges & Objectives |
|---|---|---|
| Core Goal | Replicate a proprietary MLaaS model (functional knowledge). | Protect proprietary model’s confidentiality & intellectual property (IP). |
| Key Constraints | Lack of secret training data, Limited query budget (cost, rate limits). | Preventing unauthorized model replication & data exfiltration. |
| Information Gathering Method | Sole reliance on model’s black-box outputs. | Securing model internals & data flows. |
| Efficiency Metric | Minimize queries to maximize extracted model fidelity. | Maximize attacker’s query cost, limit info per query, detect attacks. |
| Ethical/Security Implications | IP infringement, Copyright violations, Patent infringement, Unfair competition. | Data privacy issues, Vulnerabilities from LLM outputs, Unauthorized redistribution. |
| Typical Techniques (Adversary) | Active learning (uncertainty, diversity), Universal thief datasets. | On-premises LLMs, Secure RAG, Sandboxing, Data anonymization, Encryption, Access Control. |
| KAB Focus | Efficient extraction of functional knowledge from a deployed model. | Efficient protection of model’s internal knowledge and behavior. |
From the adversary’s perspective, the KAB in AME is defined by two primary constraints. First, the attacker typically operates without access to the secret training data or domain-specific knowledge about its distribution [15,45]. This absence of foundational knowledge necessitates reliance solely on the model’s output for information gathering. Second, and crucially for MLaaS, adversaries must minimize the number of queries to the proprietary service due to inherent billing structures (pro rata costs) and rate limits, which also trigger security alerts [15,45]. This “computational cost” limitation makes efficient information acquisition paramount. The severity of this bottleneck is evident in scenarios where naive querying strategies, such as using uniform noise, yield extremely low agreement scores (e.g., 10.62% on CIFAR-10 for image classification), highlighting the inadequacy of indiscriminate data acquisition [15].
The KAB in MLaaS security, when compared to data scarcity in KGs or annotation costs in clinical NLP, presents unique characteristics centered around query costs and intellectual property concerns [15]. While data scarcity and annotation costs relate to the direct unavailability or expensive creation of raw data for model training, MLaaS KAB is focused on the efficient and covert extraction of knowledge from a deployed, proprietary model. Query costs are a direct financial and operational barrier imposed by the service provider on the act of knowledge acquisition itself, rather than an intrinsic cost of data generation. Furthermore, the motivation behind AME often extends beyond merely understanding a model’s behavior; it frequently aims at intellectual property (IP) infringement. Successful model extraction can lead to severe consequences for MLaaS providers, including copyright violations, patent infringement, unauthorized redistribution, and unfair competition, particularly in high-stakes domains such as the pharmaceutical industry [45]. These IP concerns underscore the economic and strategic value embedded within proprietary models, making their extraction a distinct threat.
For MLaaS providers, the KAB manifests as the challenge of protecting model confidentiality and preventing data exfiltration, ensuring that “no data is sent to third parties” [48]. This involves mitigating risks stemming from LLM training data privacy issues, insecure user prompts, vulnerabilities with LLM-generated outputs, and issues with LLM agents [48]. To counter AME and uphold MLaaS security, various architectural choices and theoretical foundations are employed. These include secure LLM deployment strategies such as on-premises LLMs for maximum control, secure Retrieval-Augmented Generation (RAG) to manage data flow, sandboxing for execution isolation, data anonymization and PII scrubbing for privacy, differential privacy to inject noise and protect individual data points, robust access control mechanisms, encryption for data in transit and at rest, comprehensive logging for auditing, and red-teaming strategies to proactively identify vulnerabilities [48]. These measures collectively aim to raise the KAB for adversaries by increasing query costs, limiting information gain per query, and introducing uncertainty or noise into outputs, while simultaneously safeguarding the model’s IP.
Despite advancements, current research on AME and MLaaS security exhibits certain limitations. Some analyses, while detailing the adversary’s goals, do not extensively characterize the security vulnerability aspect or thoroughly analyze the defense mechanisms of MLaaS models [15]. There is also a lack of specificity regarding the types of MLaaS APIs and their security features that an adversary might encounter, which could inform more targeted defensive strategies [15]. Furthermore, critical issues like query costs and IP infringement are often implied rather than explicitly categorized with a “Defect Label,” hindering a systematic assessment of their impact and mitigation [45]. Future research should focus on a more detailed characterization of the KAB from the MLaaS provider’s perspective, analyzing the effectiveness and trade-offs of proposed secure deployment strategies, and developing explicit frameworks for categorizing and addressing the unique economic and legal ramifications of AME. This would involve a deeper exploration of API-specific vulnerabilities and defenses, moving beyond generic security practices to tailored solutions for different MLaaS offerings.
2.3.2 Binary Code Analysis and Cybersecurity
The knowledge acquisition bottleneck (KAB) in binary code analysis primarily manifests as a profound difficulty in achieving generalizable semantic understanding and invariance to the myriad nuisances introduced by various compilation processes [24]. Unlike human reverse engineers who can infer high-level functionality despite low-level differences, machine learning models often struggle to abstract away compilation artifacts to identify true semantic equivalence. This challenge is acutely observed in “out-of-domain (OOD) architectures and libraries” in assembly clone search, where models fail to generalize across unseen processor architectures (e.g., MIPS, PowerPC) or libraries (e.g., Putty, Coreutils) [24].
KAB Challenges in Binary Code Analysis
| Challenge Category | Specific Issue | Impact on Knowledge Acquisition & Generalization |
|---|---|---|
| Compilation Variability | Inability to generalize to unseen compiler variants | Models trained on limited toolchains fail on low-resource/proprietary architectures due to data scarcity. |
| Function Inlining | Significantly perturbs binary code structure, increases sequence length, obscures semantic patterns. | |
| Compiler-Specific Injected Code | Adds considerable noise and complexity, causes architectural mismatch for semantic similarity. | |
| Feature Reliance | Reliance on Structural Features (e.g., CFGs) | Susceptible to noisy information from diverse architectures, poor performance in OOD scenarios. |
| Semantic Understanding | Achieving Generalizable Semantic Understanding | Difficulty abstracting away compilation artifacts to identify true semantic equivalence across binaries. |
| Architectural Mismatch | - | Models struggle to capture true semantic similarity due as surface forms are profoundly altered by compilation. |
| Transferability | Poor Generalization to Out-of-Domain (OOD) | Models trained on one environment (e.g., x86) perform poorly on others (e.g., MIPS, PowerPC). |
Several specific issues contribute to this bottleneck, stemming from the underlying assumptions and architectural choices of current methods:
- Inability to Generalize to Unseen Compiler Variants: Existing models, often trained on limited toolchain variants (e.g., x86 and ARM), exhibit poor generalization to low-resource or proprietary processor toolchains. This limitation is primarily due to
data scarcity, which impedes the effective generation of diverse training data encompassing the vast landscape of compiler optimizations and target architectures [24]. The theoretical foundation often assumes a degree of input homogeneity that is simply not present in the real-world binary space. - Challenges from Function Inlining: Compiler optimizations, such as function inlining, significantly perturb the binary code structure. This introduces noise and substantially increases the sequence length of code segments, thereby obscuring critical elements and making it difficult for models to identify core semantic patterns [24]. The architectural choices in many models are not robust enough to discern salient features from such heavily optimized and lengthened sequences.
- Compiler-Specific Injected Code: Compilers frequently inject additional code for various purposes, including memory optimization or bounds checking. This injected code adds considerable noise and complexity, leading to
architectural mismatchissues where models struggle to capture true semantic similarity due to extraneous elements [24]. - Reliance on Structural Features: Methods that predominantly rely on structural features, such as Control-Flow Graphs (CFGs), are particularly susceptible to noisy information generated by diverse architectures and compiler optimizations. This dependency on mutable structural properties leads to suboptimal performance in OOD scenarios, as these structural features are not invariant to the compilation process [24]. The underlying assumption that structural similarity correlates directly with semantic similarity is often flawed in binary analysis.
In contrast to the highly specific challenges of binary analysis, other areas of software engineering and code understanding address different facets of the KAB. For instance, agent_kb_leveraging_cross_domain_experience_for_agentic_problem_solving focuses on resolving software engineering issues and “code repair tasks” at the source code level using the SWE-bench benchmark [33]. While this involves code analysis, its focus remains on fixing bugs within source code, and it does not directly confront the challenges posed by “binary code analysis,” “out-of-domain architectures and libraries,” or “compiler variants” that are central to the binary analysis KAB. Similarly, graph_based_approaches_and_functionalities_in_retrieval_augmented_generation_a_comprehensive_survey discusses GraphCoder, a Retrieval-Augmented Generation (RAG) framework for code completion. GraphCoder leverages Code Context Graphs (CCGs) to capture relationships like control flow and data dependencies for improved code LLM performance. Its language-agnostic design, tested on Python and Java, demonstrates versatility in utilizing structured code knowledge [71]. However, this framework, despite its advancements in acquiring and utilizing structured code knowledge, does not explicitly address the unique KAB manifestations related to OOD architectures, compiler variations, or function inlining in assembly clone search [71].
The fundamental distinction lies in the level of abstraction and the nature of semantic understanding required. Source-code-focused approaches (e.g., agent-based bug fixing or graph-based RAG for code completion) operate in a relatively controlled environment where high-level linguistic structures are largely preserved. Their domain-specific adaptations and architectural choices, such as using CCGs [71], are tailored to extract semantics from human-readable code. Binary analysis, conversely, demands distilling invariant semantics from low-level, highly variable, and often obfuscated representations where compilation choices profoundly alter the surface form without changing underlying functionality. The observed performance differences highlight that current models’ theoretical foundations and architectural choices often assume an idealized representation, which breaks down when faced with the inherent “noise” of compiled binaries.
A critical assessment reveals that current methodologies in binary analysis are limited by their inability to learn truly invariant representations of code semantics across diverse compilation environments. Future research must prioritize developing robust feature extraction techniques that are explicitly designed to be insensitive to compilation nuisances, rather than implicitly assuming their absence. This involves exploring novel model architectures capable of disentangling semantic information from extraneous structural and stylistic variations introduced by compilers. Addressing the data scarcity problem for low-resource architectures through techniques like few-shot learning, meta-learning, or advanced data augmentation strategies also represents a crucial area for improvement [24]. Ultimately, overcoming the KAB in binary analysis requires moving beyond superficial structural similarities to a deeper, more generalizable understanding of program behavior, akin to a human reverse engineer’s cognitive abilities, irrespective of the specific compilation context. This will necessitate architectural innovations that can learn and abstract away the impact of compiler optimizations, function inlining, and injected code to achieve true semantic equivalence.
3. Analytical and Measurement Frameworks for Understanding the KAB
Understanding and mitigating the Knowledge Acquisition Bottleneck (KAB) in Large Language Models (LLMs) necessitates sophisticated analytical and measurement frameworks that can both peer into the internal mechanisms of these models and rigorously evaluate their capacity for knowledge acquisition and utilization.
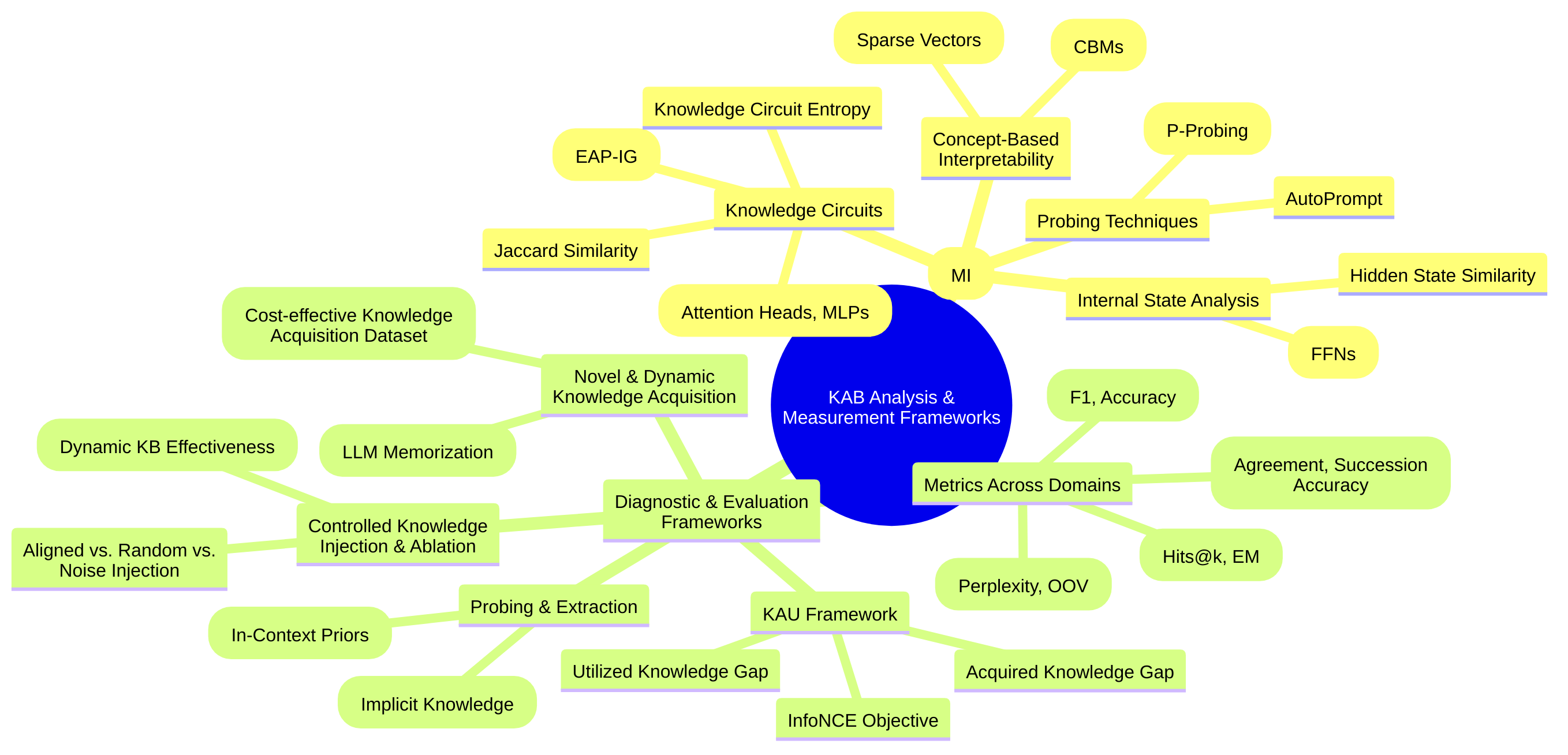
This section synthesizes the principal approaches used to analyze the KAB, categorizing them into mechanistic interpretability (MI) and diagnostic and evaluation frameworks. While MI approaches aim to unravel the intricate internal workings of LLMs to illuminate how knowledge is acquired, stored, and processed, diagnostic frameworks focus on quantifying what knowledge is present and how effectively it is utilized in various tasks and contexts. Together, these methodologies provide a comprehensive lens through which to identify the root causes of the KAB and inform the development of more effective solutions.
Mechanistic interpretability (MI) serves as a critical tool for transparently analyzing the internal dynamics of LLMs, offering insights into their knowledge integration and processing. A prominent MI approach involves the analysis of “knowledge circuits,” which are defined as sparse computational subgraphs within the model responsible for storing and processing specific knowledge [34]. Techniques such as Edge Attribution Patching with Integrated Gradients (EAP-IG) are employed to quantify the importance of individual computational paths, assigning a score $S(e)$ to an edge $e=(u,v)$ as: \(S(e)=\left(z_u^{\prime}-z_u\right) \frac{1}{m} \sum_{k=1}^m \frac{\partial L\left(z^{\prime}+\frac{k}{m}\left(z-z^{\prime}\right)\right)}{\partial z_v}\) This allows for the identification of critical circuits that contribute significantly to a model’s performance on a given task [34]. Graph-theoretical metrics, such as Jaccard Similarity and Knowledge Circuit Entropy $H(\mathcal{C})=-\sum_{e\in E_{\mathcal{C}}} P(e)\log P(e)$, further quantify the structural evolution and functional specialization of these circuits, revealing how knowledge becomes more centralized and efficient during training, particularly in larger models [34]. Beyond circuit analysis, probing techniques, including Position-Based Probing (P-Probing) and AutoPrompt, diagnose how factual knowledge is stored and elicited, often assuming a linear encoding within hidden embeddings [43,73]. Concept-based interpretability, exemplified by methods that discover sparse concept vectors in latent spaces or through Concept Bottleneck Models (CBMs), also explores how human-interpretable concepts are represented and influence model decisions [32,54]. Internal state analysis metrics, such as “knowledge entropy” within Feed-Forward Networks (FFNs), provide quantitative diagnostics for the KAB by revealing how the sparsity of memory coefficients impacts new knowledge acquisition and forgetting rates [69]. While these MI approaches offer deep insights into how LLMs learn and organize knowledge, many are limited by their computational demands, generalizability across model sizes, and often rely on simplifying assumptions like linear knowledge encoding or synthetic data [34,73].
Complementing mechanistic insights, diagnostic and evaluation frameworks rigorously quantify the extent of knowledge acquisition and, crucially, its utilization. A notable framework, \methodabbrev, directly measures the “acquired knowledge gap” and the more critical “utilized knowledge gap” by constructing downstream tasks exclusively from knowledge that a model demonstrably possesses [53]. This framework leverages techniques like soft-prompting to extract parametric knowledge and employs objectives such as InfoNCE, maximizing the similarity between queries and relevant documents, to assess utilization: \(\mathcal{L}(k) = -\log \frac{\exp(\mathrm{sim}(q, d^+))}{\sum_{d \in \{d^+,d^-_1,\dots,d^-_m\}} \exp(\mathrm{sim}(q, d))}\) This approach has demonstrated that while larger models acquire more knowledge, the gap in their ability to utilize that knowledge persists [53]. Other probing and extraction techniques, including AutoPrompt and AutoElicit, diagnose implicit knowledge and its consistency during in-context learning [19,43]. Controlled knowledge injection and ablation studies, as seen in frameworks like those in [7] and KnowMap [44], differentiate genuine knowledge utilization from mere data augmentation effects and highlight the critical role of efficient knowledge access and retrieval. For assessing the acquisition of novel and dynamic information, frameworks like the Cost-effective Knowledge Acquisition Dataset (CKAD) utilize LLM judges to evaluate knowledge gained from recently published content, ensuring the targets are genuinely new [4]. A broad spectrum of metrics are employed across domains, including traditional NLP metrics (F1 score, accuracy), knowledge graph-specific metrics (Hits@k, Exact Match), and efficiency metrics (perplexity, Out-Of-Vocabulary rates) [16,49].
The synergy between mechanistic interpretability and diagnostic evaluation frameworks is essential for a holistic understanding of the KAB. MI provides a window into the internal “how,” explaining the computational structures and dynamics underpinning knowledge, while diagnostic frameworks quantify the external “what” and “how well,” assessing the practical application of that knowledge. For instance, while MI identifies that knowledge circuit entropy decreases during training, indicating centralization [34], diagnostic frameworks can then quantify how effectively this centralized knowledge translates into performance on specific tasks, as exemplified by \methodabbrev [53]. A key challenge across both areas is the current reliance on static benchmarks and the potential biases introduced by LLM-as-a-judge evaluations, which often lack the depth to explain why knowledge utilization failures occur [4,20]. Future research must bridge the gap between internal mechanistic insights and external performance evaluation by developing unified, dynamic, and prescriptive diagnostic tools. These tools should move beyond measuring outcomes to pinpoint the precise stages in the knowledge pipeline where acquisition or utilization bottlenecks arise, considering both linear and non-linear representations, thereby advancing towards a more intelligent and knowledge-efficient generation of AI systems.
3.1 Mechanistic Interpretability Approaches
Mechanistic interpretability (MI) aims to unravel the internal mechanisms of Large Language Models (LLMs) to understand how they acquire, store, and process knowledge, thereby illuminating the underlying causes of the Knowledge Acquisition Bottleneck (KAB). These analytical frameworks contribute to a deeper understanding of the KAB by providing transparent insights into the internal dynamics of LLMs’ knowledge integration and processing, facilitating problem identification, and informing the development of more targeted solutions.
Mechanistic Interpretability Techniques for LLM KAB
| Technique / Approach | Core Idea / Mechanism | Application / Insight for LLM KAB | Limitations / Challenges |
|---|---|---|---|
| Knowledge Circuits | Identifies sparse computational subgraphs responsible for specific knowledge. | Reveals dynamic re-organization & specialization of internal graphs, shows knowledge centralization. | Computationally demanding, assumes topological changes drive knowledge. |
| EAP-IG | Quantifies causal importance of individual computational paths/edges. | Locates critical paths for knowledge, shows how components contribute to performance. | High computational cost, complexity. |
| Knowledge Circuit Entropy | Measures topological centralization of knowledge flow. | Stable downward trend (centralization) linked to efficient new knowledge integration. | Focuses on structural flow, not semantic content. |
| Probing Techniques | Trains auxiliary models to extract linearly encoded knowledge. | Diagnoses factual knowledge storage & extractability. | Assumes linear encoding, may miss complex non-linear representations. |
| P-Probing | Linear classifier on final hidden layer outputs to predict attributes. | Quantifies linear encoding of attributes, shows impact of augmentation. | Relies on linearity assumption, may be limited. |
| AutoPrompt | Automates trigger token generation for knowledge elicitation. | Reveals inherent model knowledge without fine-tuning, provides lower bound. | Generated prompts often uninterpretable, method can be brittle. |
| Concept-Based Interpretability | Identifies human-interpretable concepts in latent spaces. | Helps interpret AI-discovered strategies, allows control over model decisions. | Linearity assumption for concepts, challenging to establish causality. |
| AlphaZero Concept Discovery | Sparse vectors in latent space via convex optimization. | Makes black-box AI concepts (M-H set) interpretable & transferable to humans. | Limited to linear encoding, methodological flaws possible. |
| Concept Bottleneck Models (CBMs) | Explicitly learns human-interpretable concepts in a dedicated layer. | Allows direct intervention & understanding of model decisions, enhances steerability. | Design challenge to ensure concept meaningfulness, linearity assumption. |
| Internal State Analysis | Quantifies specific properties of internal representations. | Diagnoses how internal memory organization impacts continuous learning. | Focuses on specific components (e.g., FFNs), may not be holistic. |
| Knowledge Entropy (FFNs) | Measures sparsity of memory coefficients in FFNs. | Correlates with new knowledge acquisition & forgetting rates, diagnoses plasticity. | Does not fully encompass all internal model components. |
| Hidden State Similarity | Compares cosine similarity of hidden states for knowledge content. | Reveals LLM struggle to differentiate aligned vs. random knowledge (inefficient encoding). | Limited to cosine similarity, may ignore other differences. |
This section synthesizes various MI approaches, comparing their theoretical foundations, architectural choices, and the specific insights they offer into the KAB.
A prominent approach to understanding knowledge acquisition within LLMs involves analyzing “knowledge circuits,” defined as sparse computational subgraphs within the model that are most relevant to storing and processing specific knowledge [34]. This framework allows for a granular diagnosis of how new knowledge is integrated into an LLM during continual pre-training. The methodology for discovering and analyzing these circuits often employs Edge Attribution Patching with Integrated Gradients (EAP-IG) to assign an importance score to each edge in the model’s computation graph. The importance score $S(e)$ for an edge $e=(u,v)$ is computed as: \(S(e)=\left(z_u^{\prime}-z_u\right) \frac{1}{m} \sum_{k=1}^m \frac{\partial L\left(z^{\prime}+\frac{k}{m}\left(z-z^{\prime}\right)\right)}{\partial z_v}\) where $z_u$ and $z’_u$ represent clean and corrupted activations, $L$ is the negative logit difference loss function, and $m$ is the number of integrated gradient steps [34]. Circuits are then identified by selecting the top $n$ edges with the highest absolute EAP-IG scores, ensuring these selected edges collectively reproduce a significant portion (e.g., over 70%) of the whole model’s performance on a specific task [34].
Graph-theoretical metrics are crucial for quantifying the structural evolution and functional specialization of these knowledge circuits. Jaccard Similarity measures the structural consistency of edge and node sets between intermediate training checkpoints and the final circuit, indicating how stable the circuit’s composition is over time [34]. Knowledge Circuit Entropy, calculated as $H(\mathcal{C})=-\sum_{e\in E_{\mathcal{C}}} P(e)\log P(e)$ (where $P(e)$ is the normalized absolute importance score of an edge $e$), quantifies topological centralization. A lower entropy value suggests greater centralization of knowledge within fewer, more critical computational pathways [34]. Analysis using these metrics has revealed that knowledge circuit entropy exhibits a stable downward trend, characterized by an initial rapid “formation phase” followed by a slower “optimization phase.” Larger models tend to reach this phase shift more quickly, leading to improved circuit performance in later stages [34]. Component analysis further tracks the distribution and specialization of attention heads (e.g., mover, relation, mixture heads) and activated edges across layers, showing shifts in their proportions and layer-wise activation during different acquisition phases [34]. These findings suggest that the KAB is not merely a capacity issue but involves dynamic re-organization and specialization of internal computational graphs, which become more centralized and efficient over training, particularly for relevant new knowledge [34].
Beyond circuit analysis, probing techniques represent a class of MI approaches designed to diagnose how LLMs store and process factual knowledge, typically assuming linear encoding in their hidden embeddings [54,73]. Position-Based Probing (P-Probing), for instance, involves training an auxiliary linear classifier on the LLM’s final hidden layer outputs to predict target attributes from specific token positions. The accuracy of this classifier quantifies the extent of linear encoding for the attribute’s value [73]. This method has shown that knowledge augmentation during pretraining significantly improves P-probing accuracies, suggesting more robust and linear knowledge encoding [73]. Complementary to this, AutoPrompt serves as a non-invasive probing technique that elicits knowledge from LMs using automatically generated prompts without introducing additional learned parameters, thereby providing a more reliable lower bound on the model’s inherent knowledge [43]. However, a critical limitation of these probing methods is their reliance on the assumption of linearly encoded knowledge, which may overlook more complex, non-linear representations within the model’s hidden states [54,73]. Furthermore, AutoPrompt’s generated prompts often “lack interpretability,” hindering understanding of why certain triggers are effective [43].
Concept-based interpretability offers another perspective, assuming that concepts are linearly encoded in the latent space. For example, in AlphaZero, concepts are discovered as sparse vectors in the latent space via convex optimization, minimizing their $L_1$ norm subject to concept-specific constraints. A novelty metric based on spectral analysis helps identify concepts unique to the AI’s “language,” and concept amplification validates their influence on model behavior by nudging latent representations [54]. Similarly, Concept Bottleneck Models (CBMs) explicitly design individual neurons within a Concept Bottleneck Layer (CBL) to learn specific, human-interpretable concepts, allowing for direct intervention and understanding of the model’s decision-making [32]. However, these approaches also face limitations regarding the linearity assumption, the potential for methodological flaws in capturing complex neural representations, and challenges in establishing definitive causal links between concepts and predictions [54].
Internal state analysis metrics provide quantitative diagnostics for the KAB. “Knowledge entropy” quantifies the sparsity of memory coefficients within Feed-Forward Networks (FFNs), which are conceptualized as key-value memories within transformer architectures [69]. A spikier coefficient distribution (lower knowledge entropy) signifies that gradient updates are concentrated on specific positions, making these memory vectors more susceptible to overwriting during new knowledge acquisition. This entropy consistently decays during pretraining and correlates strongly with knowledge acquisition and forgetting rates, directly diagnosing the KAB by revealing how the model’s internal memory organization hinders continuous learning [69]. The focus on FFNs, however, means it does not fully encompass the complex interactions of all internal model components.
Hidden state similarity analysis is another diagnostic tool, particularly for understanding the processing of injected knowledge. By comparing the cosine similarity of hidden states when an LLM is fed “aligned knowledge” versus “random knowledge,” researchers can determine if the model effectively differentiates and utilizes the specific knowledge content. Findings show high cosine similarities, suggesting that LLMs often struggle to distinguish between aligned and random knowledge at a microscopic level, indicating a lack of interpretability and inefficient knowledge encoding [7]. This analysis, however, is limited to cosine similarity, potentially ignoring differences in some dimensions [7]. For more specific symbolic representations, metrics such as state variance, number of effective bits, and number of constant zero bits have been used to diagnose the Symbol Stability Problem (SSP) in latent spaces, highlighting instability that can undermine symbolic reasoning [28].
Broader classifications of MI methods categorize them into “observation-based methods” (e.g., probes, Logit Lens, sparse representation) which project internal information into understandable forms, and “intervention-based methods” (e.g., causal mediation analysis, activation patching) which directly perturb LLMs to identify critical components and causal connections [30]. These methods apply to analyzing “Modular Region” hypotheses (e.g., MLPs or attention heads) and “Connection” hypotheses, such as knowledge circuits [30]. However, the reliability of causal tracing for knowledge localization has been questioned, indicating a methodological flaw in some existing approaches [20].
While some interpretability efforts focus on high-level, human-legible explanations, such as the C$^4$ model’s “transparency” via output inspection and explanation generation [58], these often lack the technical detail required for mechanistic analysis of neural networks. Similarly, conceptual frameworks drawing analogies to cognitive science, such as “quantum tunneling” with “meta-characteristics” or InfoBot’s dual pathways, primarily offer metaphorical or theoretical insights without providing concrete computational methods for internal component analysis [37,46,56]. Visual interpretability methods, like GradCAM for heatmaps in VQA [61], or attribution maps and learned filter visualizations for image analysis [39], are effective for visual domains but do not directly probe the knowledge circuits of LLMs. Specialized datasets, like fictional QA datasets, can serve as crucial resources for controlled studies of memorization, which is a prerequisite for more advanced mechanistic interpretability [60].
In summary, mechanistic interpretability frameworks provide diverse tools to scrutinize the KAB. Knowledge circuit analysis offers deep insights into the dynamic, structural, and functional evolution of knowledge integration [34]. Probing and concept discovery methods reveal aspects of linear knowledge encoding, though they may overlook non-linear complexities [54,73]. Metrics like knowledge entropy quantify the parametric knowledge distribution and its impact on acquisition and forgetting [69]. However, many of these approaches are limited by computational resources, generalizability to larger models, and their reliance on assumptions such as linear encoding or the use of synthetic data [34]. Future research should focus on developing methods to identify non-linear concept representations, enhancing the reliability of knowledge localization, and exploring how to bridge abstract theoretical models with concrete, verifiable computational mechanisms within LLMs to address the fundamental questions of what factors shape knowledge circuits and how knowledge in the human brain compares to text sequences [12]. The integration of diverse MI techniques will be crucial for a holistic understanding of the KAB and for informing the development of LLMs that acquire and retain knowledge more effectively.
3.2 Diagnostic and Evaluation Frameworks for Knowledge Utilization
The accurate diagnosis and rigorous evaluation of knowledge acquisition and utilization are paramount for advancing research in large language models (LLMs) and other AI systems. While conventional task-specific metrics offer performance insights, a deeper understanding necessitates frameworks that can isolate and quantify specific knowledge gaps, particularly distinguishing between knowledge that a model possesses and knowledge it can effectively apply.
Diagnostic & Evaluation Frameworks for Knowledge Utilization
| Framework/Approach | Core Mechanism / Goal | KAB Insight / Measurement | Key Metrics / Examples | Limitations / Challenges |
|---|---|---|---|---|
| KAU Framework | Differentiates “acquired” vs. “utilized” parametric knowledge. | Quantifies the “knowledge acquisition-utilization gap.” | InfoNCE loss, Top-1 retrieval accuracy, Performance on model-generated tasks. | Relies on model’s ability to generate coherent knowledge, specific to PLMs. |
| Probing & Extraction | Elicits implicit knowledge without fine-tuning. | Diagnoses inherent knowledge & its consistency during ICL. | Automated prompts (AutoPrompt), MLE/Energy Statistic (AutoElicit), Q-Probing accuracy. | Linearity assumption, lack of interpretability for prompts, diagnostic not prescriptive. |
| Controlled Knowledge Injection & Ablation | Systematically compares aligned vs. random/noise injection. | Distinguishes genuine knowledge utilization from data augmentation. | F1, precision, recall, accuracy, Training-validation loss gap (KnowMap). | Difficult to disentangle true knowledge effects from noise, often task-specific. |
| Evaluation of Novel & Dynamic Knowledge | Assesses acquisition/utilization of genuinely new information. | Measures ability to learn & apply new, evolving world knowledge. | Win Rate (WR), LC_WR (CKAD), Exact Match, NLL, MCQ accuracy (FictionalQA). | LLM-as-a-judge bias, limited to static benchmarks, “leaky generalization.” |
| Mechanistic Interpretability (MI) | Analyzes internal knowledge processing (how knowledge is used). | Explains mechanisms rather than direct measurement of utilization gap. | Knowledge circuit entropy, causal tracing, concept bottleneck activation. | Primarily explanatory, not directly quantitative for utilization gap, computationally intensive. |
| Domain-Specific Metrics | Tailored to specific tasks & knowledge types. | Quantifies performance on specific knowledge-intensive tasks. | NLP (F1), KG (Hits@k), Efficiency (Perplexity), Model Agreement, Policy Accuracy. | Not directly comparable across domains, may obscure underlying KAB issues. |
One pioneering framework, known as \methodabbrev, addresses this challenge by meticulously measuring the “acquired knowledge gap” and the more critical “utilized knowledge gap” in pre-trained language models (PLMs) [53]. The core assumption of \methodabbrev is that true knowledge utilization can only be assessed in controlled environments where confounding factors, such as arbitrary crowd-sourced tasks or insufficient signal, are eliminated. To achieve this, \methodabbrev employs a multi-stage methodology: first, it extracts parametric knowledge from a pre-trained model ($\mathcal{M}\theta$) as a set of data instances ($\mathcal{D}^\theta$) that the model can solve zero-shot, often leveraging soft-prompting techniques to predict entities or relations [53]. Subsequently, a downstream task ($\mathcal{K}^\theta$) is meticulously constructed *exclusively* from this model-generated knowledge ($\mathcal{D}^\theta$). This architectural choice ensures that success on $\mathcal{K}^\theta$ relies *solely* on utilizing the model’s internal parametric knowledge, rather than external cues. The evaluation then proceeds by fine-tuning the model on $\mathcal{K}^\theta\mathrm{train}$ using the InfoNCE objective, a technique commonly employed for learning discriminative embeddings, where the loss function is defined as: \(\mathcal{L}(k) = -\log \frac{\exp(\mathrm{sim}(q, d^+))}{\sum_{d \in \{d^+,d^-_1,\dots,d^-_m\}} \exp(\mathrm{sim}(q, d))}\) This objective maximizes the similarity between queries and relevant documents while pushing away irrelevant ones [53]. Performance on $\mathcal{K}^\theta_\mathrm{test}$ (measured by top-1 retrieval accuracy) directly indicates the model’s ability to utilize its acquired knowledge. Experiments with models like OPT and GPT-Neo demonstrated that while scaling model size increases acquired knowledge, the utilization gap persists, highlighting a fundamental limitation in current PLMs’ ability to operationalize their internal representations [53].
Beyond \methodabbrev, several other frameworks contribute to understanding knowledge utilization, though with varying assumptions and methodologies.
1. Probing and Extraction of Parametric Knowledge:
The concept of soft-prompting, central to \methodabbrev, finds parallels in other probing techniques. AutoPrompt employs a gradient-guided search to automatically generate “trigger tokens” for classification tasks, reformulating them as fill-in-the-blank problems to elicit knowledge from masked language models (MLMs) without fine-tuning [43]. This technique diagnostically identifies the most effective phrasing to reveal existing knowledge, albeit sometimes resulting in ungrammatical prompts that lack human interpretability [43]. Similarly, AutoElicit diagnoses LLMs’ implicit knowledge during in-context learning (ICL) by extracting in-context priors and posteriors using Maximum Likelihood Estimation (MLE) and quantifying consistency with an energy statistic [19]. This approach helps determine if LLMs approximate Bayesian inference during ICL, revealing that some models, like GPT-3.5-turbo, struggle to consistently imitate linear models, indicating an approximation error in knowledge representation or application [19]. Q-Probing from [73] also assesses knowledge extractability by training linear classifiers on LLM embeddings of entities (e.g., person names) to predict associated biographical attributes. This method reveals a strong correlation between attribute linkage to an entity name and effective knowledge extraction, suggesting that names function as crucial retrieval “hooks” for stored knowledge [73].
2. Controlled Knowledge Injection and Ablation Studies:
To diagnose the genuine impact of knowledge injection, the framework in [7] proposes an ablation protocol. It compares performance under aligned knowledge injection, random knowledge injection, and noise injection, measuring metrics like F1 score, precision, recall, and accuracy, alongside an analysis of the training-validation loss gap. This systematic comparison serves to distinguish true knowledge utilization from mere data augmentation effects, often revealing that performance gains are not always attributable to the structured knowledge itself [7]. KnowMap evaluates the effectiveness of dynamically constructed knowledge bases for task adaptation by fine-tuning an embedding model using the InfoNCE loss function to optimize knowledge retrieval for an LLM backbone [44]. This diagnostic highlights that ineffective retrieval can actively degrade performance, underscoring the critical role of efficient knowledge access and utilization [44]. Similarly, GRAIL employs ablation studies to quantify the impact of fine-tuning (SFT) and interactive inference on graph comprehension and knowledge utilization in graph-retrieval augmented LLMs. It measures accuracy and F1 score, with GPT-4 acting as a semantic equivalence judge, demonstrating that removing these components significantly degrades performance and efficiency [63]. Ski also uses RAG, SFT, and CPT strategies with various metrics (F1, nDCG, Recall) to evaluate the outcome of synthetic knowledge ingestion for enhancing LLMs [5].
3. Evaluation of Novel and Dynamic Knowledge Acquisition:
For assessing the acquisition and utilization of genuinely novel information, the CKAD (Cost-effective Knowledge Acquisition Dataset) framework is proposed. It simulates biomedical expert consultations using PubMed Central articles published after an LLM’s knowledge cutoff [4]. This ensures that the evaluation targets truly new knowledge, employing LLM judges (GPT-4o, GPT-4-Turbo) and metrics like Win Rate (WR) and Length-Controlled Win Rate (LC_WR) to quantify knowledge gaps [4]. The study on fictional QA datasets also provides a multi-faceted diagnostic to understand how LLMs acquire and utilize factual knowledge from training data, measuring verbatim memorization (Exact Match), factual memorization via Negative Log-Likelihood (NLL) on Q&A pairs, and Multiple Choice Question (MCQ) accuracy. This framework controls for pre-existing model knowledge and reveals “leaky generalization,” suggesting an intermingling of factual and distributional learning [60,68].
4. Mechanistic Interpretability for Knowledge Utilization:
While many frameworks focus on external performance, understanding how knowledge is utilized internally requires mechanistic interpretability. The framework presented in [30] categorizes knowledge utilization into memorization, comprehension & application, and creation, investigated through hypotheses like the Modular Region, Connection, Reuse, and Extrapolation hypotheses. This diagnostic aims to identify knowledge-encoding components (e.g., specific MLP layers, attention heads) and knowledge circuits within LLMs [30]. However, it primarily explains mechanisms rather than providing quantitative diagnostic metrics for knowledge gaps or assessing parametric knowledge application in downstream tasks using objectives like InfoNCE. Similarly, concept_bottleneck_large_language_models proposes CB-LLMs and evaluates them based on faithfulness (human studies on Activation and Contribution Faithfulness), steerability (quantified by setting concept neuron activations), and generation quality (perplexity), aiming to make the model’s internal concept utilization explicit and interpretable [32].
5. Metrics for Knowledge Utilization and Efficiency in Various Domains: A broad spectrum of metrics are employed across different domains to assess knowledge utilization, including:
- Traditional NLP Metrics: F1 score, accuracy, precision, recall remain standard for evaluating tasks like biomedical relation extraction, MRC, QA, NER, and text generation [2,9,16]. ROUGE and METEOR are used for summarization and Q&A [2].
- Knowledge Base/Graph Specific Metrics: Hits@k for Knowledge Base Completion (KBC) [49], and Exact Match (EM) accuracy for Open-Domain QA and LAMA knowledge probing [1]. KG construction quality is assessed via human evaluation of precision and coverage comparisons with external resources like Paperswithcode [11,66]. Specific KG quality dimensions include completeness, accuracy, timeliness, availability, and redundancy, often evaluated through recall and precision against ground truth [55]. Novel metrics like “Domain Specificity” quantify the proportion of extracted domain-relevant triples not present in open KGs [66].
KGValidatorleverages LLMs and contextual augmentation (Wikidata, Web) to assess the factual accuracy of KGC outputs, demonstrating enhanced diagnostic capability through external knowledge utilization [40]. - Efficiency and Uncertainty Metrics: Perplexity and Out-Of-Vocabulary (OOV) rates are used to quantify knowledge utilization and the severity of vocabulary acquisition bottlenecks, respectively [16]. Retrieval Count (RC) quantifies the efficiency of knowledge acquisition by measuring reliance on external searches [27]. Perplexity also serves as an indicator of uncertainty in adaptive elicitation strategies, complemented by Expected Calibration Error (ECE) and Brier Score to assess confidence-accuracy alignment [13].
- Specialized Domain Metrics: For classical planning, metrics like successor state prediction accuracy, monotonicity violation, plan coverage, validity, and optimality are used to evaluate the acquired knowledge and its utilization by symbolic planners [28]. In model extraction, “agreement” between a secret and substitute model (defined as identical label predictions on a dataset) is used to quantify knowledge utilization efficiency [15,45].
DKAimplicitly diagnoses knowledge utilization gaps by having the LLM explicitly request specific types of knowledge through question decomposition, directly addressing the mismatch between retrieved and needed knowledge prevalent in “forward-only” systems [61].
Critique and Future Directions:
Despite these advancements, the landscape of diagnostic and evaluation frameworks for knowledge utilization faces significant limitations. A prevalent critique is the lack of comprehensiveness and the reliance on static benchmarks, which are insufficient for measuring dynamic and evolving world knowledge [20]. This leads to a methodological flaw where knowledge editing methods often show limited propagation of edited knowledge, preventing LLMs from performing deeper reasoning based on newly acquired facts [20]. The use of LLM-as-a-judge for evaluation, while offering scalability, introduces potential biases and uncalibrated confidence scores, as observed in StructSense and CKAD [4,70]. Such black-box evaluations often fail to provide why certain knowledge is utilized or not, posing interpretability challenges.
Many frameworks remain task-specific, focusing on the outcome of knowledge utilization (e.g., accuracy on QA tasks) rather than the internal mechanisms or “knowledge circuits” within the model [16,42]. This necessitates novel diagnostic tools that can pinpoint the root causes of utilization failures, potentially by integrating mechanistic interpretability with utilization metrics. Frameworks for rule-based systems, such as the coverage graph and Minimum Message Length (MML) adaptation for hierarchical assessment, offer insights into symbolic knowledge structures but are not directly applicable to deep learning models due to differing representations [67]. The challenge of evaluating knowledge systems with LLM components, designing appropriate ontologies, and understanding the relationship between evaluation and explainability remains an open research question, often requiring labor-intensive human evaluation with associated computational costs and time implications [52].
Future research should prioritize the development of dynamic, robust, and unified evaluation benchmarks that can quantitatively compare diverse knowledge acquisition and utilization methods across different categories (e.g., knowledge editing, continual learning, retrieval-based methods) [20]. There is a clear need for frameworks that go beyond measuring overall performance to offer prescriptive diagnostics of where in the knowledge pipeline failures occur, rather than simply quantifying the lack of difference. Advancements in quantifying knowledge entropy decay suggest a promising avenue for understanding capacity for new knowledge, but its relation to parametric knowledge extraction and utilization gaps needs further exploration [69]. The ultimate goal is to move towards evaluation methodologies that not only measure what a model knows and utilizes, but also how and why, guiding the development of more intelligent and knowledge-efficient AI systems.
4. Solution Frameworks for Attacking the Knowledge Acquisition Bottleneck
The Knowledge Acquisition Bottleneck (KAB) represents a persistent challenge in Artificial Intelligence, hindering the development of intelligent systems by requiring extensive manual effort to gather, structure, and formalize knowledge. Addressing this bottleneck necessitates diverse solution frameworks that span methodologies from automated data generation and structured knowledge representation to advanced model learning paradigms, human-AI collaboration, and cognitively inspired architectures.
This section provides a high-level overview of these frameworks, highlighting their fundamental contributions, underlying principles, and the synergistic interplay crucial for scalable and efficient knowledge acquisition.
Broadly, these solutions can be categorized into frameworks focused on efficient data and resource generation, structured knowledge representation and management, leveraging and enhancing model-centric intelligence, integrating human expertise for quality and guidance, and cognitively inspired approaches that seek deeper understanding of intelligence itself. While each category offers distinct advantages, modern research increasingly emphasizes their integration to create more robust and adaptive AI systems.
Data-centric and Resource Creation Frameworks primarily tackle the KAB by minimizing the manual effort in data annotation and resource generation [10,57]. These approaches include automated data annotation and synthesis, often leveraging large language models (LLMs) to generate high-quality synthetic datasets or augment existing ones, thereby scaling up training data production [5,60,63,68]. Weak and distant supervision further reduce annotation burdens by automatically generating noisy labels from existing knowledge or heuristics, although robust denoising mechanisms are often required [9,16]. Active learning strategically selects the most informative data points for human annotation, optimizing human effort and accelerating model training [6,57]. Techniques like data augmentation, sampling, and refinement enhance the utility of available data, addressing issues such as class imbalance and optimizing computational efficiency [65,73]. Crucially, these frameworks also encompass the direct creation and management of structured knowledge resources, such as knowledge graphs (KGs) and benchmark datasets, which are foundational for many AI applications.
Knowledge Graph Construction and Management Frameworks are dedicated to transforming heterogeneous, often unstructured, data into semantically rich, structured representations [3,74]. These frameworks have evolved from labor-intensive rule-based and symbolic systems, which offer high precision within well-defined domains, to statistical and neural approaches leveraging information extraction techniques for greater scalability. The advent of generative knowledge graph construction, particularly with LLMs, marks a significant shift towards higher automation, enabling direct generation of structured knowledge from natural language and even facilitating autonomous ontology evolution [17,23,66]. Ensuring data quality and managing uncertainty are paramount in this domain, with frameworks integrating validation mechanisms and confidence scores to enhance trustworthiness.
Pre-trained Language Model (PLM) and Large Language Model (LLM) Integration Frameworks have revolutionized knowledge acquisition by positioning LLMs as central to Knowledge Engineering workflows [59,75]. LLMs passively acquire vast amounts of knowledge during pre-training, but active elicitation frameworks (e.g., AutoPrompt) are designed to query and extract this embedded knowledge efficiently [43]. More critically, various knowledge injection frameworks actively integrate external knowledge into LLMs, bridging their static pre-training with dynamic, up-to-date information. These include KG augmentation strategies, Retrieval-Augmented Generation (RAG) systems that couple LLMs with external memory for real-time information access [20,71], and knowledge editing/continual learning techniques that directly modify LLM parameters to internalize new facts without full retraining [68]. Agentic and modular frameworks further orchestrate LLMs within broader systems, often with external components for specialized tasks. The focus is also on knowledge disentanglement and interpretability, aiming to make LLM-acquired knowledge transparent and controllable [32,50,61].
Model-Centric and Transfer Learning Frameworks mitigate the KAB by enabling models to learn transferable representations and reason more efficiently about their own knowledge [26]. This often involves leveraging knowledge acquired from diverse sources or previous tasks to reduce reliance on extensive task-specific data. Metacognitive knowledge, allowing models to reason about their own learning processes, and meta-learning, which trains models to learn efficient adaptation algorithms, are key concepts [68]. Different approaches facilitate architectural transfer (e.g., Net2Net) or cross-domain experience sharing (e.g., AgentKB) [33,62]. The Information Bottleneck principle guides the learning of maximally compressed yet informative representations, enhancing transfer and exploration across various domains like Reinforcement Learning and semantic representation learning [24,56]. Deep Neural Network (DNN) extraction frameworks demonstrate how functional knowledge can be transferred by replicating a target model’s behavior, making implicit knowledge explicit [15].
Hybrid and Human-in-the-Loop (HIL) Frameworks are crucial for balancing the efficiency of automation with the precision and nuanced judgment of human expertise [3,55]. Strategies include active learning for efficient annotation, expert validation for quality control, interactive refinement and steerability of AI models (e.g., TeachMe, MemPrompt, LBM), and human-guided data generation for bootstrapping initial knowledge [50,57,70]. These frameworks also leverage implicit human expertise embedded in pre-trained models and structured knowledge bases, and integrate symbolic and statistical learning (neuro-symbolic AI) to combine interpretability with pattern recognition capabilities [16,28,36].
Cognitive and Neurosymbolic Approaches seek to address the KAB by integrating principles inspired by human cognition into AI system design, aiming for more interpretable, adaptable, and robust knowledge acquisition. This includes operationalizing concepts like metacognition—the ability of systems to monitor and control their own cognitive processes—to enhance learning and self-reflection [58,68,69]. Frameworks like AlphaZero’s concept discovery aim to make black-box AI knowledge interpretable and transferable to human experts, bridging the human-AI knowledge gap [54]. Neurosymbolic architectures combine neural network strengths with symbolic reasoning, often centered around Knowledge Graphs or constraint-driven logic, to achieve systematic generalization, robustness, and explainability [28,36,59].
Reinforcement Learning (RL) and Exploration Frameworks enable agents to acquire knowledge through active interaction with their environment, particularly for efficient exploration and policy transfer. The Information Bottleneck principle, as leveraged by InfoBot and IBOL, helps in learning compressed, task-relevant representations and intrinsically motivated exploration, especially in sparse reward settings [35,56]. RL-inspired techniques, such as R1-Searcher++, empower LLMs to dynamically decide between internal and external knowledge sources, continuously memorizing retrieved information to enhance their internal state [27]. GRAIL applies RL for efficient exploration of knowledge graphs, using process-level rewards to guide complex reasoning tasks [63].
Finally, Adversarial Knowledge Acquisition Frameworks represent a contrasting perspective, highlighting the vulnerabilities and challenges related to knowledge ownership and protection. These frameworks, often leveraging query-based model extraction and active learning strategies with “universal thief datasets,” aim to replicate proprietary machine learning models from black-box oracles, underscoring the efficiency with which knowledge can be acquired, even for malicious purposes [15,45]. While not direct solutions to the KAB in a constructive sense, they illuminate the sophistication of knowledge extraction techniques and the critical need for robust defensive measures to safeguard AI intellectual property.
Despite significant advancements across these diverse frameworks, several common challenges persist. These include the computational cost and scalability inherent in training large models or performing iterative processes, the persistent problem of noise and hallucination in automatically generated or weakly supervised data, and limitations in generalizability, especially in long-tail or highly specialized domains [3,12,16,60,63]. The “knowledge acquisition and utilization gap” in pre-trained models, the difficulty in maintaining current world knowledge, and issues of bias and lack of provenance also remain critical concerns [7,20,55]. The ethical implications, ranging from IP theft to the propagation of biased information, underscore the broader societal responsibility in developing these technologies.
Future research must focus on developing more integrated and robust frameworks that synergistically combine these approaches. This involves improving noise handling, reducing reliance on expensive proprietary models, enhancing the interpretability and explainability of acquired knowledge, and developing adaptive systems capable of lifelong learning and managing dynamic information streams. Bridging the “cognitive gap” between human associative thinking and AI’s knowledge representation, fostering greater collaboration between humans and AI, and designing transparent and trustworthy systems will be paramount for truly overcoming the Knowledge Acquisition Bottleneck and unlocking the full potential of artificial intelligence.
4.1 Data-Centric and Resource Creation Frameworks
Addressing the knowledge acquisition bottleneck (KAB) often involves shifting focus from traditional manual annotation to more efficient, data-centric strategies that either automate the labeling process or optimize the use of available data. These frameworks contribute to making knowledge acquisition more scalable and less reliant on intensive human effort [10,57]. They span various methodologies, from generating entirely synthetic datasets to intelligently selecting data points for human annotation, and from leveraging existing knowledge bases to refining raw information.
Data-Centric and Resource Creation Techniques for KAB
| Technique Category | Core Mechanism | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Automated Annotation & Synthesis | LLMs or other models generate synthetic labeled data. | Reduces manual labeling effort, scales data production. | GRAIL (graph data), FictionalQA (Q&A), Ski (QCA), R1-Searcher (task instances). | Relies on generative model quality/bias, generalizability to real-world. |
| Weak & Distant Supervision | Automatically labels data using existing KBs or heuristics. | Reduces annotation burden, generates noisy labels at scale. | KRDL (from KBs), MatSKRAFT (structured datasets), KeLM Corpus (Wikidata). | Inherent noise, potential incompleteness of labels, requires denoising. |
| Active Learning (AL) | Iteratively selects most informative samples for human annotation. | Optimizes human effort, accelerates training, reduces annotation cost. | Uncertainty sampling (LC, Entropy), K-center, DFAL, PU-ADKA, CEGA. | Computational cost of retraining, choice of acquisition function, warmstart quality. |
| Data Augmentation & Refinement | Expands or optimizes existing datasets. | Addresses data scarcity, class imbalance, improves robustness. | Power-law guided (MatSKRAFT), Multiplicity/Permutation (PLMs), Concept Generation (CB-LLMs). | Can introduce noise, requires careful design to avoid spurious correlations. |
| Knowledge Resource Creation | Builds/improves structured knowledge assets. | Provides foundational knowledge, enables automated KGC/KE. | SAC-KG (domain KG), Graph-Powered Databases (RAG), Bench4KE (benchmarks). | Often requires initial manual effort/validation, scalability for continuous updates. |
One prominent approach involves automated data annotation and synthesis, which aims to generate labeled data or synthetic data with minimal human intervention. Frameworks like GRAIL utilize large language models (LLMs) such as GPT-4o to synthesize high-quality graph reasoning datasets by simulating graph exploration operations. This process retains only instances leading to correct answers, effectively creating process-supervised data without direct human annotation [63]. Similarly, the FictionalQA dataset generation pipeline employs LLMs like GPT-4o to create controlled, high-quality synthetic Q&A data for studying LLM memorization, validating answers for feasibility and correctness through automated checks [60]. The Self-Tuning framework also uses GPT-4 to generate QA pairs and self-supervised knowledge-intensive tasks from raw documents, bypassing human annotation for each learning example and augmenting documents with diverse task types like summarization and NLI [68]. The Synthetic Knowledge Ingestion (Ski) method automates fine-grained knowledge representation generation by having a pioneer LLM (e.g., GPT-3.5-turbo) create hypothetical questions and answers from $n$-gram knowledge contexts, ensuring detailed relevance and diverse representation [5]. R1-Searcher integrates rejection sampling in its SFT cold-start phase to synthesize high-quality training instances that adhere to specific formatting rules, and also enriches an internal knowledge resource through continuous memorization of retrieved external information [27]. MatSKRAFT, designed for materials science, employs property-specific algorithms that encode domain expertise through multi-dimensional pattern recognition to identify properties and resolve ambiguities, combined with power-law guided data augmentation to address frequency imbalances in material properties [65]. For scholastic information extraction, EneRex uses weakly-supervised learning with automated data generation based on syntactic patterns to create noisy ground truth for entities like source code links and dataset usage, though it often requires subsequent manual refinement for facets with significant noise [51]. While highly scalable, a common limitation across LLM-based synthetic data generation methods is their reliance on powerful, often closed-source, LLMs, which introduces computational costs and potential biases from the generative model itself [60,63,68]. The generalizability of findings based on synthetic data to real-world scenarios also remains a challenge [60].
Weak and distant supervision frameworks reduce annotation burden by automatically generating noisy labels from existing knowledge resources or heuristic rules. The Knowledge-Rich Deep Learning (KRDL) framework integrates and denoises various forms of weak supervision, including distant supervision from knowledge bases like GDKD and data programming using labeling functions derived from simple rules or domain expertise [16]. This approach automatically tags training examples for relation extraction by assuming if a relation holds in a knowledge base (e.g., Freebase, Wikidata), then any sentence containing both entities in text is a positive instance for that relation [1,9,12,72]. For instance, the KeLM Corpus construction uses distant supervision to align Wikidata triples with Wikipedia text, achieving coverage of millions of triples and sentences, but acknowledges the noise introduced in this process [1]. MatSKRAFT further combines distant supervision with property-specific algorithms and data augmentation, leveraging structured datasets like INTERGLAD for initial labeling and resolving ambiguities with domain expertise encoded in rule-based systems [65]. The primary limitation of weak and distant supervision is the inherent noise and potential incompleteness of the generated labels, which requires subsequent denoising or robust modeling techniques [1,16,72].
Active learning (AL) is a powerful data-centric strategy that iteratively reduces annotation burden by intelligently selecting the most informative unlabeled data points for human annotation [57]. The process typically begins with a set of “warmstart samples,” a small, randomly acquired initial labeled dataset (e.g., 2% of the total dataset), used to train an initial model [57]. Subsequently, the model identifies examples where its predictions are uncertain, or which would maximize information gain. These are then sent to a human oracle for labeling. This iterative cycle of selection, annotation, and model retraining continues until a desired performance level or budget limit is reached [6]. Key to active learning are uncertainty estimation and acquisition functions. Common uncertainty measures for classification include Least Confidence (LC), which selects examples with the lowest predicted probability, and for sequence labeling, Maximum Length-Normalized Log Probability (MNLP) [57]. More advanced methods, such as Bayesian Active Learning by Disagreement (BALD), measure uncertainty based on the disagreement among multiple Monte Carlo (MC) draws from a stochastic model, exemplified by DO-BALD (using Monte Carlo Dropout) and BB-BALD (using Bayes-by-Backprop) [57]. For instance, the NER mutation framework improves dataset quality by selectively re-annotating instances ranked by confidence or similarity to known errors, significantly reducing the gap between single and full double annotation with minimal additional effort [25]. In graph-based domains, CEGA applies active sampling to acquire graph neural network behaviors efficiently, using an interim model to guide the selection of informative nodes under budget constraints [45]. PU-ADKA extends this by optimizing expert selection based on availability, knowledge boundaries, and cost within a fixed budget, demonstrating efficient domain knowledge acquisition for LLMs in sensitive areas [4]. The use of “universal thief datasets” combined with pool-based active learning also helps adversaries extract deep neural networks within a limited query budget, by selecting small yet informative sample sets from large public datasets like ImageNet or WikiText-2 [15]. A primary limitation of AL is the computational cost of retraining models in each round, especially for deep learning models [57]. The practical challenge of choosing an optimal acquisition function without online comparison also remains, as well as the sensitivity to the quality of initial warmstart samples [45,57].
Data augmentation, sampling, and refinement techniques focus on expanding or optimizing the utilization of existing datasets. For instance, in scientific text summarization, data sampling on large datasets like Arxiv (down to 2% of articles) and adaptive tokenization (focusing on top 500 significant tokens) significantly boost training efficiency and reduce computational load [2]. MatSKRAFT employs power-law guided data augmentation to address long-tail distributions in material properties by synthetically generating values to amplify rare properties while preserving statistical distributions [65]. Physics of Language Models highlights data augmentation strategies like multiplicity, permutation, and fullname augmentation to enhance linguistic diversity and robustness, implicitly providing automated data annotation by creating varied training signals from limited facts, leading to substantial QA accuracy improvements (e.g., from 9.7% to 96.6% on bioS for some attributes with multiplicity augmentation) [73]. Concept Bottleneck LLMs (CB-LLMs) leverage LLMs for automated concept generation and then employ Automatic Concept Scoring (ACS) using sentence embeddings to generate pseudo-labels for training, further refined by Automatic Concept Correction (ACC) to improve label quality, yielding significant accuracy boosts (e.g., 3.5% average improvement for CB-LLMs) without manual annotation [32]. This demonstrates a shift towards LLM-driven data curation. For knowledge graph construction, source selection and filtering, along with robust data cleaning frameworks, are crucial to ensure the quality and trustworthiness of data, tackling structural and semantic inconsistencies using rule-based, statistical, or machine learning methods [3]. Efforts like “purifying and pruning” large external knowledge bases into “Conceptual Knowledge” from sources like Wikidata and WordNet exemplify refinement strategies to overcome knowledge complexity mismatch [7].
Knowledge resource creation and management encompasses efforts to build or improve structured knowledge assets such as knowledge graphs (KGs), ontologies, and benchmark datasets. The general domain of Knowledge Graph Construction itself aims to automatically create and enrich structured data from unstructured text, addressing data scarcity and manual annotation needs [74]. Frameworks like SAC-KG achieve unsupervised domain KG construction using a domain corpora retriever that segments and ranks sentences by entity frequency to provide relevant context to LLMs, reducing manual effort significantly [66]. In RAG systems, “Graph-Powered Databases” are foundational, with methods to transform plain text into KGs using instruction-tuned language models or specialized tools like KG-FiD, GLBK, and ATLANTIC [71]. Automated rule base construction from web corpora using information extraction also contributes to knowledge representation for logical reasoning systems [75]. For ontology creation, approaches like the KNOW ontology simplify resource creation by focusing on universally understood concepts and explicitly materializing common relationships, reducing the need for complex graph traversal [36]. Furthermore, creating high-quality benchmark datasets is critical for evaluation. Examples include the manually crafted Gold Standard Dataset for benchmarking automated Competency Question generation in Bench4KE [14], the CORLL dataset for computing resources in EneRex [51], and the OMIn benchmark for operations and maintenance intelligence [48]. The creation of the Cost-effective Knowledge Acquisition Dataset (CKAD) by GPT-4o with manual validation also provides a structured resource for evaluating domain-specific LLMs [4]. While manual efforts in creating gold standards are significant, they are essential for reliable evaluation.
A specific technique attempting to relax strict annotation requirements for Word Sense Disambiguation (WSD) is the “one sense per Wikipedia Category” hypothesis [10]. This principle, leveraged by frameworks like OneSeC, assumes that all occurrences of a word within a specific Wikipedia category page refer to the same sense. This allows for automated annotation of noun occurrences within these category texts, leading to large-scale sense-annotated corpora with high estimated quality (e.g., SEW with over 160M sense annotations and >90% precision) [10]. Other automatic methods for sense annotation include exploiting Wikipedia hyperlinks, using parallel corpora (EuroSense), or language-independent approaches like Train-o-Matic, often balancing coverage with a degree of noisiness [10].
In all, these data-centric frameworks make diverse underlying assumptions. Automated synthesis heavily relies on the generative capabilities and biases of LLMs, assuming they can produce coherent and factually accurate data. Weak/distant supervision assumes that noise can be effectively managed and that existing knowledge bases provide a sufficient signal. Active learning’s effectiveness hinges on the model’s ability to accurately estimate uncertainty and the human oracle’s reliability. Resource creation and refinement strategies typically assume the availability of raw data or existing knowledge to process, and some involve manual curation steps for quality control.
Critically, while these frameworks significantly reduce direct human annotation effort, they introduce new challenges. The quality of automatically generated or weakly supervised data can suffer from noise and error propagation, demanding robust denoising mechanisms or advanced modeling that can tolerate imperfect labels [16,72]. The reliance on LLMs for data generation can lead to computational costs, data dependency issues on proprietary models, and limitations in generalizability to novel or highly specialized domains [32,60,63]. Even active learning, while efficient, faces challenges in choosing optimal acquisition functions and computational overhead due to iterative retraining [57]. Furthermore, foundational tasks like semi-automatic mapping definition in KG construction remain an area for improvement to further reduce manual effort [3]. Future research should focus on developing more robust and adaptive frameworks that can effectively combine these strategies, improve noise handling in automated labels, reduce LLM dependency for cost-effectiveness, and design more intelligent active learning strategies that consider the dynamic nature of knowledge and resource constraints. Addressing the generalizability of synthetic data and the optimal integration of various data sources, including for lifelong learning scenarios where models continuously update their knowledge, also represent key areas for advancement [34,44,64].
4.2 Knowledge Graph Construction and Management Frameworks
Knowledge Graph Construction (KGC) and its continuous management are pivotal in addressing the knowledge acquisition bottleneck, transforming heterogeneous data into semantically rich, structured representations [3,74]. This section categorizes and analyzes various KGC frameworks based on their core methodologies, tracing their evolution and highlighting their strengths and weaknesses in automation, scalability, and handling diverse data types.
Core Methodologies and Framework Categorization
KGC frameworks can be broadly categorized by their underlying methodological principles: rule-based/symbolic, statistical/neural (Information Extraction-based), and generative.
- Rule-based and Symbolic Frameworks: These frameworks primarily rely on pre-defined ontologies, explicit rules, and formal specifications for knowledge extraction and representation. For instance, early versions of YAGO combined Wikipedia with WordNet, evolving to YAGO 4 which enforces consistency with schema.org/Bioschemas via SHACL constraints and manual mappings [3]. The
OpenReq-DDframework exemplifies ontology-based methods in Requirements Engineering, using pre-defined ontologies as “gold-standards” for relation extraction, inferring relationships based on semantic and hierarchical structures [6]. TheVerifiercomponent inSAC-KG, while part of an LLM-driven system, is rule-based, employing over 7000 criteria to detect and correct errors in generated triples, addressing format, quantity, and logical inconsistencies [66].- Strengths: Such approaches excel in precision within well-defined domains where rules are unambiguous and ontologies are stable. They offer strong consistency guarantees.
- Weaknesses: They suffer from high “expert dependency” and are “time-consuming” to design, generate, and maintain, leading to “maintainability” issues as domains evolve [6]. The rule-based nature of verification can also be limited, potentially failing to capture complex errors beyond predefined rules [66].
- Statistical and Neural (Information Extraction-based) Frameworks: This category encompasses methods that leverage statistical models and deep learning for core Information Extraction (IE) tasks crucial for populating KGs.
A generic KGC pipeline involves stages such as Data Acquisition & Preprocessing, Ontology Management, Knowledge Extraction (KE), Entity Resolution & Fusion, Quality Assurance, and Knowledge Completion [3].
* Knowledge Extraction (KE): This typically involves Named Entity Recognition (NER) to identify entity mentions, Entity Linking (EL) to connect them to existing KG entities, and Relation Extraction (RE) to determine relationships among them [3,74].
* Frameworks: DeepKE is a toolkit providing implementations for NER, RE, and Attribute Extraction (AE), supporting various scenarios from standard supervised settings to low-resource, document-level, and even multimodal extraction [38]. The SciNLP-KG framework employs learning-based models, including a hybrid NLI model for inter-entity relation extraction, a BERT-Siamese Network for coreference, and an unsupervised term2vec model for “related” entities, to construct KGs from scientific papers [11]. EneRex extracts technical entities from scholarly articles to enrich existing KGs, though it acknowledges the open challenge of standardizing extracted entities [51]. Many specific KGC approaches, such as dstlr, AI-KG, CovidGraph, and AutoKnow, integrate various NLP tools and machine learning components within their pipelines [3].
* Strengths: These methods significantly automate the extraction process, enabling scalability from vast unstructured text sources and handling diverse data types. They have been foundational in building large-scale KBs like DBpedia, NELL, and Freebase [9].
* Weaknesses: Traditional pipeline-based approaches often suffer from “error propagation,” where errors in earlier stages negatively impact subsequent ones [11,23]. Many still rely on pre-defined schemas, making schema alignment and handling evolving ontologies challenging [38].
- Generative Knowledge Graph Construction and the Role of LLMs: The field has seen a notable shift towards “generative knowledge graph construction” leveraging sequence-to-sequence (Seq2Seq) frameworks and large language models (LLMs) [23]. This paradigm aims to overcome the “error propagation and poor adaptability” of traditional methods by unifying various NLP tasks into a single generative process, directly generating structural knowledge (e.g., triples) from input sequences [23].
- LLMs as Automatic Constructors: LLMs are emerging as “skilled automatic constructors” for KGs [66]. Frameworks like
SAC-KGexploit LLMs in an iterative, entity-induced tree search algorithm to construct multi-level domain KGs, achieving 89.32% precision and 81.25% domain specificity [66]. LLMs like GPT-3 can perform “robust knowledge base construction” through information extraction, including NER and RE, by carefully crafted prompts [18]. - LLMs as KG Builders and Controllers: LLMs demonstrate the ability to generate KGs from natural language instructions in various formats, leveraging their internal “model knowledge” and “generative inference” [12]. This “Instruction-driven Knowledge Extraction” reduces the need for laborious labeling and enables identifying previously unseen entity types and relations [12]. Beyond construction, LLMs also act as “KG Controllers,” automating query template enhancement and facilitating “Text to Logical Query Parsing” by converting natural language into structured query formats (e.g., SPARQL) [12,52]. LLMs are also used in RAG systems, where instruction-tuned LLMs extract entities and relations from text to construct graphs as auxiliary databases [71].
- Strengths: Generative KGC offers high automation, flexibility, and the potential to synthesize new knowledge even when information is insufficient, reducing the impact of component-wise errors inherent in pipelines [12,23].
- Weaknesses: A significant limitation is the “risk of introducing incorrect knowledge (hallucination)” [12]. While LLMs can build KGs, their correctness rate for common domains is often 70-80% and significantly lower for long-tail domains, indicating “reliability” and “accuracy” deficiencies compared to state-of-the-art small models for precise extraction tasks [12].
- LLMs as Automatic Constructors: LLMs are emerging as “skilled automatic constructors” for KGs [66]. Frameworks like
Evolution of KGC Frameworks Over Time
The evolution of KGC frameworks reflects a continuous effort to enhance automation, scalability, and adaptability. Initially, KGs were often manually curated or extracted from highly structured sources (e.g., Wikipedia infoboxes by DBpedia) [3]. This progressed to statistical and rule-based methods for extracting knowledge from unstructured text, as seen in NELL’s semi-supervised learning approach [3]. The advent of deep learning further propelled this, enabling more sophisticated entity and relation extraction from diverse textual data. The most recent and significant shift is towards “generative knowledge graph construction” [23], where LLMs are employed not just for extraction but for actively synthesizing knowledge and even generating entire graph structures, moving beyond the traditional pipeline to a more unified approach.
Foundational vs. Specialized Frameworks
- Foundational Frameworks for General KG Construction: These frameworks aim to build comprehensive KGs from diverse sources.
construction_of_knowledge_graphs_state_and_challengesprovides a detailed overview of such approaches, including DBpedia (structured data from Wikipedia), YAGO (Wikidata and WordNet integration), NELL (incremental text-based construction),AutoKnow(Amazon’s product KG with GNNs for relation discovery), andSAGA(multi-source data integration with incremental updates). These frameworks integrate various stages like data acquisition, ontology management, knowledge extraction, entity resolution, and quality assurance.- Strengths: They are designed to integrate heterogeneous data from multiple sources, some offering incremental update capabilities.
AI-KG, for instance, integrates research publications data using advanced NLP tools and categorical facts into an ontology built on SKOS, PROV-O, and OWL [3]. - Weaknesses: Many struggle with “scalability” to a large number of sources and robust support for “incremental updates,” often resorting to batch recomputation [3]. “Comprehensive support for entity fusion and quality assurance is often lacking or rudimentary,” and there is a “lack of open tools” among more advanced frameworks, hindering research and development [3].
- Strengths: They are designed to integrate heterogeneous data from multiple sources, some offering incremental update capabilities.
- Specialized Frameworks for KG Extension: These frameworks focus on augmenting existing KGs by identifying and integrating new knowledge. The framework proposed in [31] explicitly focuses on extending KGs via “entity type recognition.” It involves a four-stage process: data preparation, entity type recognition (aligning concepts at schema and instance levels), a “specially designed extension algorithm” to integrate knowledge, and performance assessment. This mechanism handles subclasses and merges entities based on property-based similarity. Knowledge Base Completion (KBC), a critical aspect of KG extension, uses techniques like probabilistic latent variable models, embedding models (e.g., TransE and its numerous extensions), and tensor decomposition to predict missing facts [9].
better_together_enhancing_generative_knowledge_graph_completion_with_language_models_and_neighborhood_informationframes KGC as a sequence-to-sequence task, where an encoder-decoder Transformer model generates missing tail entities, leveraging the head node’s 1-hop neighborhood for enhanced context.- Strengths: They directly address KG incompleteness, improve coverage, and leverage existing KG structures. The generative approach to KBC enhances completeness by combining LLM semantic understanding with explicit graph structural context [49].
- Weaknesses: Conflict resolution strategies, like prioritizing the reference KG, may limit “generalizability” [31]. KBC methods face “scalability issues” and “computational costs,” particularly for complex probabilistic inferences and tensor decomposition on large KBs [9].
- Autonomous Ontology Evolution: This category focuses on frameworks that enable dynamic, automatic updating and maintenance of KG ontologies.
Evo-DKDis a novel dual-decoder framework for “autonomous ontology evolution” in LLMs [17]. It proposes ontology edits and natural-language justifications, validates them through consistency checks and justification cross-checks, and integrates validated edits in a “closed-loop autonomous updating” system [17]. LLMs exhibit capabilities in “automated construction of conceptual hierarchies, ontological category expansion, attribute completion, ontology alignment, and concept normalization” [12]. TheKNOWontology itself is designed as a foundational framework tailored to augment LLMs, promoting “semantic interoperability” and “type compatibility” through SDKs and various serializations [36].- Strengths: Autonomous evolution addresses the long-standing problem of manual ontology maintenance, adapting KGs to new knowledge and changing domains. This enhances the long-term viability and relevance of KGs.
- Weaknesses: The core challenge remains the reliability of LLM-generated edits, given the “hallucination” problem. Ensuring the consistency and accuracy of LLM-generated formal knowledge with existing KGs is an ongoing research question [52].
Data Quality, Cost-Effectiveness, and Structured Nature
Maintaining data quality is paramount in KGC and management. The uncertainty_management_in_the_construction_of_knowledge_graphs_a_survey paper highlights an “ideal data integration pipeline” comprising knowledge alignment, fusion, and consistency checking, which explicitly considers various confidence scores (extraction, source, overall) and provenance information to handle uncertainty [55]. KGValidator offers a flexible framework for automatically validating KG triples using LLMs, integrating external knowledge (LLM inherent, RAG, Wikidata, web search) as context to determine triple validity and provide reasons, serving as a critical quality gate [40].
Graph-based approaches inherently offer a “structured nature” and can be “cost-effective” for various tasks. CEGA proposes a cost-effective approach for graph-based model extraction and acquisition, particularly relevant for GNN models applied to clinical KGs. It offers an alternative to training from scratch, addressing issues like “incomplete local databases” and “data heterogeneity” in Electronic Health Records, enabling “ontology-informed learning” [45]. Agent KB organizes experiences in a hierarchical knowledge graph, using semantic and structural indices for efficient retrieval and relational reasoning [33]. MatSKRAFT constructs a comprehensive materials database by linking entities within and across scientific tables using “intra-table” and “inter-table linking,” demonstrating effective structural integration [65]. The “coverage graph” in [67] acts as an internal mechanism for dynamically managing logical rules, showcasing the utility of graph structures for knowledge dynamics.
Limitations and Future Research
Despite significant advancements, several challenges persist across KGC and management frameworks. A common limitation is “scalability,” particularly for many-source integration and incremental updates, with many approaches still relying on batch recomputation [3]. “Human expertise dependency” and “manual effort” remain bottlenecks in traditional KGC pipelines and ontology management, affecting resource constraints and hindering full automation [6,44,55]. The “hallucination” problem in LLMs poses a critical “reliability” and “accuracy” deficiency for generative KGC, especially in long-tail domains [12,52]. The “lack of open tools” for advanced KGC frameworks (e.g., AutoKnow, SAGA) restricts broader research and development [3]. Furthermore, “schema heterogeneity” and robust “knowledge fusion” mechanisms, especially when integrating highly diverse data types or managing conflicts, continue to be complex challenges [3]. Future research should focus on developing unified frameworks that seamlessly incorporate confidence scores from all stages of knowledge integration, mitigating LLM hallucination, enhancing the generalizability of rule-based verification, and promoting open-source development of scalable, adaptive KGC and ontology evolution tools. Addressing these areas will be crucial for truly overcoming the knowledge acquisition bottleneck.
4.3 Pre-trained Language Model (PLM) and Large Language Model (LLM) Integration Frameworks
Large Language Models (LLMs) and their predecessors, Pre-trained Language Models (PLMs), have fundamentally reshaped the landscape of knowledge acquisition, acting as both implicit knowledge repositories and active agents for knowledge extraction and integration. They are increasingly conceptualized as central to Knowledge Engineering (KE) workflows, offering the potential to enhance, replace, or add KE components by leveraging their capacity to capture existing world knowledge from vast unstructured data [59,74,75].
Passive Knowledge Capture vs. Active Elicitation
LLMs primarily acquire knowledge passively during their extensive pre-training on colossal datasets, encoding this information into their parameters [30]. This process allows them to internalize factual knowledge and linguistic patterns, with the evolution of “knowledge circuits” within the model’s layers offering insights into how this knowledge is structurally embedded [34]. The concept of “knowledge entropy” suggests that the model’s plasticity and stability for acquiring new knowledge change dynamically throughout pre-training, indicating that mid-stage checkpoints might be optimal for further knowledge incorporation [69]. Mixed training approaches, where models are trained from scratch on a blend of raw text and question-answer (QA) pairs, have been shown to make stored knowledge more readily extractable through Q&A, even for out-of-distribution scenarios, albeit sometimes at the cost of faithful text reproduction [73].
In contrast to passive capture, active elicitation focuses on querying LLMs to retrieve or approximate specific knowledge. AutoPrompt exemplifies this by automatically generating prompts to activate and extract knowledge from frozen LLMs without requiring fine-tuning, effectively transforming tasks into “fill-in-the-blank” problems. This demonstrates the LLM’s inherent capacity to serve as a knowledge base, capable of performing complex tasks with high accuracy solely through optimized prompting [43]. However, the automatically generated prompts can sometimes lack interpretability, hindering human understanding of the elicitation mechanism [43]. Another approach, AutoElicit, leverages LLMs to approximate expert knowledge for constructing prior distributions in predictive models, enabling flexible knowledge elicitation through natural language interaction [19]. Soft-prompting has also been employed for diagnostic purposes, aiding in the evaluation of existing parametric knowledge within LLMs [53].
Knowledge Injection Frameworks: Aligning and Integrating External Knowledge
LLM Knowledge Integration Frameworks
| Integration Approach | Core Mechanism | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Passive Knowledge Capture | LLMs internalize knowledge during pre-training. | Creates vast implicit knowledge base, contextual understanding. | BERT, T5, Llama (pre-trained weights), Knowledge Circuits, Knowledge Entropy. | Static knowledge, utilization gap, catastrophic forgetting, interpretability. |
| Active Elicitation | Query LLMs to retrieve/approximate specific knowledge. | Makes implicit knowledge explicit, reduces fine-tuning effort. | AutoPrompt (trigger tokens), AutoElicit (expert priors), Soft-prompting. | Prompts can be uninterpretable, relies on linearity assumption, brittleness. |
| Knowledge Injection: KG Augmentation | Infuses structured knowledge from KGs into LLMs. | Enhances factual accuracy, reduces hallucination, improves reasoning. | K-BERT, GLM (implicit), KeLM (verbalization), KEPLER (objective). | Semantic loss, interference between signals, “ineffective utilization.” |
| Knowledge Injection: RAG | Couples LLMs with external, non-parametric memories/web. | Provides up-to-date, domain-specific info, reduces hallucination. | Entity-RAG, Tree-RAG, KG-FiD, R1-Searcher (dynamic retrieval). | Scalability of memory, noisy sources, inference overhead, knowledge conflicts. |
| Knowledge Injection: KE & CL | Directly modifies/updates LLM internal parameters. | Internalizes new facts, mitigates catastrophic forgetting. | ROME, MEMIT (KE), K-Adapter, Lifelong-MoE (CL), Self-Tuning. | Side effects, limited propagation, training phases, not for black-box LLMs. |
| Knowledge Injection: Agentic/Modular | Orchestrates LLMs within broader systems with external components. | Enables specialized tasks, improves control & grounding. | StructSense (multi-agent), KNOW (neuro-symbolic synthesis), Agent KB. | Computational cost, complexity of orchestration, requires robust alignment. |
| Adaptive Elicitation | Dynamically interacts with sources/users to refine info. | Optimizes information gathering, refines acquired knowledge. | Adaptive QA (reduces uncertainty), GRAIL (KG exploration), PU-ADKA (expert feedback). | Computational demands, reliance on feedback quality, complex optimization. |
| Knowledge Disentanglement | Separates knowledge types for clarity/control. | Improves interpretability, reduces confusion, enhances steerability. | DKA (question decomposition), CB-LLMs (concept bottleneck layer). | Computational cost, linearity assumption, generalizability of disentanglement. |
To address the limitations of passively acquired, static knowledge, various “knowledge injection frameworks” have emerged to align and integrate external knowledge into LLMs. These frameworks can be broadly categorized by their approach:
- Knowledge Graph (KG) Augmentation: This prominent strategy infuses structured knowledge from KGs into LLMs, enhancing their understanding and performance on downstream tasks by combining the strengths of unstructured (contextual) and structured (factual) knowledge sources [12,74].
- Input-layer Injection: Converts KG facts into natural language descriptions, expanding the LLM’s input (e.g., K-BERT, CoLAKE) [12].
TeKGenandKeLMcorpus generate synthetic natural language text from Wikidata KGs to augment pre-training data, particularly for retrieval-based LMs [1]. A critical limitation of this approach is the potential for semantic loss and hallucination during the verbalization process [1,12]. - Intermediate-layer Injection: Integrates structured knowledge (e.g., KG embeddings) into the model at an intermediate layer, often through attention mechanisms (e.g., ERNIE, KnowBERT, KG-BART) [12]. This method attempts to preserve structural semantics more effectively but can suffer from interference between textual and structural signals [12].
- Objective-layer Injection: Injects knowledge via multi-task learning and refined loss optimization, such as KEPLER, which adds a KG embedding loss to the standard masked prediction loss, ensuring a unified encoder learns both text and entity information [12].
- Structure-Inducing Pre-training: Frameworks like
Graph-guided Masked Language Model (GLM)exploit KGs during pre-training to guide tasks like entity masking and distractor-suppressed ranking, implicitly embedding relational knowledge into the language model’s representations. This makes the model more efficient during fine-tuning and inference by obviating costly runtime retrieval, but it is less flexible for dynamic updates [42].
However, a critical re-evaluation in
revisiting_the_knowledge_injection_frameworksindicates that many existing KG integration frameworks (e.g., ERNIE, LUKE, KnowBert, K-BERT, KeBioLM) exhibit only marginal performance differences when injecting aligned knowledge compared to random knowledge or even Gaussian noise. This suggests LLMs often “fail to adequately disentangle the intricacy possessed in the external knowledge base” [7]. The paper proposes that injecting “Conceptual Knowledge” (purified and pruned knowledge from sources like Wikidata and WordNet) via simple textual prompts significantly improves accuracy and effective knowledge utilization. - Input-layer Injection: Converts KG facts into natural language descriptions, expanding the LLM’s input (e.g., K-BERT, CoLAKE) [12].
- Retrieval-Augmented Generation (RAG): A dominant explicit alignment strategy, RAG couples static LLMs with external, non-parametric memories or real-time web access, allowing them to access and synthesize up-to-date and domain-specific information without internal parameter modification [20,30].
- RAG can be single-stage (retrieving once and prepending to the prompt) or multi-stage (iterative retrieval and revision, often interleaved with Chain-of-Thought reasoning) [20].
- KGs enhance RAG by providing structured context and conceptual hierarchies (e.g., Entity-RAG, Tree-RAG, KG-FiD) [12,71].
RetroPromptdecouples knowledge into an independent external knowledge base that enriches prompts, improving LLM generalization in few-shot scenarios [12].Skileverages an LLM to generate synthetic data (QA pairs, contexts) from raw text, optimizing the retrieved content for RAG, supervised fine-tuning (SFT), and continual pre-training (CPT) to ensure the knowledge is readily “assimilable and digestible” by LLMs [5].R1-Searcherdynamically incentivizes LLMs to decide between using internal knowledge and invoking external search, and it incorporates a mechanism for the LLM to continuously internalize and memorize retrieved external information, progressively enriching its internal knowledge and reducing over-reliance on external retrieval [27].- Limitations: RAG systems face challenges such as the scalability of external memory, susceptibility to noisy or low-quality web content, considerable inference overheads for multi-stage retrieval, and potential knowledge conflicts where LLMs may favor internal over external information [20]. Poorly designed chunking in RAG can also lead to loss of document logic and contextual relationships [12].
- Knowledge Editing (KE) and Continual Learning (CL): These approaches focus on directly modifying or updating the LLM’s internal parameters.
- KE aims to alter specific, localized knowledge within the LLM’s weights without full re-training, employing meta-learning for intrinsic editability, hypernetwork editors for extrinsic updates ($\Delta\theta$), or “locate and edit” methods that target specific “knowledge neurons” or MLP layers (e.g., ROME, MEMIT) [20].
- CL enables LLMs to learn from continuous data streams while mitigating catastrophic forgetting, through methods like regularization, replay, or architectural modifications (e.g., K-Adapter, Lifelong-MoE for continual pre-training, or CL-plugin, GRACE for continual knowledge editing) [20].
Self-Tuningis a learning framework that trains an LLM to autonomously acquire new knowledge from unseen raw documents via self-supervised, knowledge-intensive tasks, inspired by the Feynman Technique. This multi-stage process focuses on ingesting new information into the LLM’s parameters and maintaining QA capabilities [68].- Limitations: KE methods often struggle with estimating side effects, can induce catastrophic forgetting, and do not always enable true knowledge propagation for reasoning. Both KE and CL typically require training phases, making them less suitable for black-box LLMs [20].
- Agentic and Modular Frameworks: These integrate LLMs into larger systems, often with external components.
StructSenseorchestrates LLMs within a multi-agent system, using an alignment agent for ontology grounding and a human-in-the-loop feedback agent to mitigate hallucination and enhance accuracy in structured information extraction [70].KNOWproposes a neuro-symbolic synthesis, providing LLMs with a restricted vocabulary to manipulate symbolic knowledge bases. This integration addresses LLM limitations like limited context windows, poor scalability, hallucination, and the static nature of their knowledge [36].Agent KBuses LLMs as experience generators, reasoners, and refiners to leverage cross-domain experience for problem-solving [33].
Adaptive Elicitation Frameworks
Adaptive elicitation frameworks leverage LLMs’ capabilities to dynamically interact with knowledge sources or users to refine acquired information. The framework introduced in adaptive_elicitation_of_latent_information_using_natural_language trains LLMs (e.g., Llama-3.1-8B) using meta-learning on diverse QA trajectories. This enables the LLM to simulate future responses and quantify how new questions reduce epistemic uncertainty, allowing it to develop sophisticated information-gathering strategies and select the most informative next queries. GRAIL implements an interactive retrieval paradigm where an LLM performs Chain-of-Thought reasoning to explore knowledge graph paths, dynamically selecting actions to retrieve relevant graph knowledge for complex reasoning tasks [63]. Furthermore, PU-ADKA enhances domain-specific LLMs by selectively engaging domain experts for feedback through an adaptive question-expert matching mechanism and Multi-Agent Reinforcement Learning, optimizing knowledge acquisition under budget constraints [4].
Knowledge Disentanglement and Interpretability
Disentangling knowledge and ensuring interpretability are crucial for reliable LLM performance. The Knowledge Acquisition Disentanglement (DKA) framework explicitly leverages a frozen LLM (LLaMA2-13B) to decompose complex visual question answering queries into simpler, targeted image-based and knowledge-based sub-questions [61]. This disentanglement allows specialized retrieval models to focus on relevant content, avoiding confusion from irrelevant elements and contrasting with general information extraction methods that might struggle with query complexity. The DKA framework is training-free, relying on the pre-trained capabilities of its components. However, its computational cost and scalability for broader open-source LLMs remain a challenge [61].
The difficulty LLMs face in disentangling external knowledge is also highlighted in revisiting_the_knowledge_injection_frameworks. To address this, Concept Bottleneck Large Language Models (CB-LLMs) introduce a human-interpretable Concept Bottleneck Layer (CBL) into black-box LLMs. Through adversarial training, CB-LLMs disentangle concept-related information from other latent representations, allowing for concept detection, controlled generation, and enhanced steerability [32].
For improved interpretability, Language Bottleneck Models (LBMs) utilize an encoder-decoder LLM architecture. An encoder LLM maps historical interactions to a concise natural-language summary of a latent knowledge state. A frozen decoder LLM then uses only this textual summary to make predictions, effectively forcing all predictive information through an interpretable bottleneck. This approach aims for human-understandable explanations while maintaining predictive performance [50]. Similarly, Evo-DKD employs a dual-decoder LLM architecture, generating both structured ontology edits and free-form natural language explanations, providing grounded rationales and mitigating hallucinations in ontology evolution [17].
Challenges in Maintaining Current World Knowledge and Reliability
LLMs confront significant challenges in maintaining current world knowledge and ensuring reliable outputs. Their knowledge, primarily acquired during pre-training, becomes static and quickly outdated [20,74]. This dynamic nature of real-world information poses a fundamental problem for knowledge acquisition.
A major concern is hallucination, where LLMs generate factually incorrect or nonsensical information, severely undermining their trustworthiness and utility, especially in domain-specific or sensitive contexts [17,36,40,48,52,59,70]. Frameworks like StructSense and KGValidator attempt to mitigate hallucination through external grounding, human-in-the-loop validation, and RAG-based integration with verified sources [40,70].
Other deficiencies include:
- Limited Domain Specificity: LLMs often perform poorly in specialized domains, lacking accuracy in numerical facts, and struggling with long-tail entities, necessitating domain-specific fine-tuning or external knowledge integration [48,55]. Domain-specific PLMs like BioBERT and SciBERT have demonstrated improved performance in their respective fields by pre-training on relevant corpora [25,51].
- Bias and Lack of Provenance: LLMs inherit biases from their vast training data and typically do not provide provenance or reliability information for extracted knowledge, hindering trustworthiness and knowledge fusion [55].
- Computational Cost and Scalability: The sheer size of LLMs leads to significant computational costs, data dependency, and scalability issues, particularly for deployment on resource-constrained systems or for iterative development in specialized domains [48,50,61,64]. Lightweight models and mutual learning paradigms (e.g.,
DWML) aim to address these concerns [8].
Probing Existing Knowledge vs. Dynamic Knowledge Injection/Acquisition
It is crucial to differentiate between frameworks designed for probing existing knowledge and those for dynamic knowledge injection or acquisition as solutions to the Knowledge Acquisition Bottleneck (KAB).
-
Probing Existing Knowledge: These frameworks aim to elicit or evaluate knowledge already embedded within the LLM’s parameters from its pre-training. Examples include
AutoPrompt, which uses automated prompt generation to query frozen LLMs for tasks like fact retrieval [43]; soft-prompting for diagnostic purposes [53];AutoElicit, which leverages LLMs to approximate expert knowledge for statistical priors [19]; and QA fine-tuning to confirm and extract knowledge stored during pre-training [73]. These methods primarily focus on utilizing the LLM’s existing capabilities. -
Dynamic Knowledge Injection or Acquisition: These frameworks actively work to add new or update knowledge within the LLM or make it accessible. This category directly addresses the KAB. Key examples include:
- RAG-based systems that provide LLMs with access to external, up-to-date information sources [7,18,20,61].
- Knowledge Editing and Continual Learning techniques that modify LLM parameters to internalize new facts or adapt to evolving data streams [20].
Self-Tuning, which trains LLMs to acquire knowledge from new documents through self-supervised tasks [68].- KG-augmented models that integrate structured knowledge during pre-training or inference [12,42].
R1-Searcher, which allows LLMs to dynamically acquire and internalize external information during interaction [27].DKAleverages LLMs for dynamic decomposition to guide knowledge acquisition from external sources [61].
The shift from purely probing existing knowledge to dynamically injecting and acquiring new knowledge is critical for enabling LLMs to overcome the KAB and remain relevant in rapidly changing environments. Future research needs to continue exploring how to balance the efficiency of training-free probing with the robustness and dynamism of explicit knowledge acquisition and integration, while also addressing inherent challenges such as hallucination, interpretability, and computational overhead.
4.4 Model-Centric and Transfer Learning Frameworks
Model-centric and transfer learning frameworks constitute a cornerstone in alleviating the Knowledge Acquisition Bottleneck (KAB) by enabling models to learn transferable representations and reason about their own knowledge more efficiently. These approaches typically reduce the reliance on extensive task-specific data by leveraging knowledge acquired from diverse sources or previous tasks.
A foundational concept in enhancing model autonomy is the integration of “metacognitive knowledge,” which allows neural networks to reason about their own learning processes and internal states [26]. For instance, meta-learning frameworks explicitly train models to learn algorithms for tasks like systematic generalization, catastrophic forgetting, and few-shot learning by optimizing a meta-objective across diverse training episodes [26]. This enables models to efficiently adapt to new, unseen tasks with minimal data, improving sample efficiency on benchmarks like Omniglot and Mini-ImageNet [26]. Similarly, Self-Tuning equips Large Language Models (LLMs) with a generalized “learning-to-learn” capability, allowing them to absorb new knowledge from raw documents through memorization, comprehension, and self-reflection, and transfer this strategy to unseen documents [68]. Declarative constraints can also inject “metacognitive knowledge” by guiding the model’s learning process with background knowledge about valid solutions [72]. The evolution of cognitive architectures towards neuro-symbolic infrastructures, such as LEIA agents, also emphasizes lifelong learning of ontological concepts and lexical material, with metacognition facilitating adaptability to novel situations [58]. Critically, while these conceptualizations highlight the potential, the precise technical mechanisms for integrating explicit “metacognitive knowledge” remain an active research area, often lacking detailed algorithmic specifications or comparative performance benchmarks against established deep learning paradigms [26,58].
Model-Centric and Transfer Learning Approaches
| Framework/Approach | Core Mechanism / Theory | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Metacognitive Knowledge | Models reasoning about their own learning/internal states. | Efficient adaptation, self-reflection, improved sample efficiency. | Meta-learning, Self-Tuning, LEIA agents. | Lack of detailed algorithmic specs, often conceptual/theoretical. |
| Net2Net | Function-preserving transformations for architectural transfer. | Accelerates training of larger networks, avoids retraining. | Net2WiderNet, Net2DeeperNet. | Limited to functional knowledge, architectural compatibility constraints. |
| AgentKB | Abstracting concrete experiences into reusable patterns. | Cross-domain experience sharing, improved problem-solving. | Variable generalization, step compression, teacher-student retrieval. | Diminishing returns in dissimilar domains, extreme OOD challenges. |
| Information Bottleneck (IB) | Learning maximally compressed yet informative representations. | Enhances transfer & exploration, learns invariant features. | InfoBot (RL), Pluvio (CVIB for binary analysis), IBOL (skill discovery). | Relies on variational approximations, hyperparameter sensitivity, domain-specific adaptations. |
| InfoBot | Regularizes goal-conditioned policies by minimizing mutual information. | Efficient exploration, robust transfer, learns “default policies.” | KL divergence as intrinsic reward. | Variational approximation challenges, $\beta$ parameter sensitivity. |
| Pluvio (CVIB) | Uses Conditional Variational IB to “forget” nuisance info. | Achieves domain-invariant representations, robust generalization for OOD. | All-mpnet-base-v2, CVIBEncoder. | Assumes “text-like” regularities in non-text data, obfuscation challenges. |
| DNN Extraction | Replicating target model’s behavior using queried data. | Transfers functional knowledge, makes implicit knowledge explicit. | Active learning, universal thief datasets. | Primarily functional transfer, not semantic insight, assumes query access. |
Different approaches to knowledge transfer and reuse are tailored to distinct problem domains and objectives. Comparing Net2Net with AgentKB illustrates this diversity:
-
Net2Net focuses on network architectural transfer [62]. It introduces function-preserving transformations ( Net2WiderNetandNet2DeeperNet) that allow expanding a pre-trained neural network (teacher) into a larger one (student) without re-initialization. Knowledge is transferred by copying weights from the teacher, withNet2WiderNetdistributing weights to new wider layers (e.g., $\mathbf{U}^{(i)}{k,j} = \mathbf{W}^{(i)}{k, g(j)}$ and $\mathbf{U}^{(i+1)}_{j,h} = \frac{1}{{x g(x) = g(j)} } \mathbf{W}^{(i+1)}_{g(j), h}$) and Net2DeeperNetinserting identity-initialized layers (e.g., using ReLU for $\phi(\mathbf{I} \phi(\mathbf{v})) = \phi(\mathbf{v})$) [62]. The core assumption is that a larger model, initialized to perform identically to its smaller predecessor, can achieve faster convergence and higher ultimate performance. Its strength lies in guaranteeing immediate performance retention and facilitating architectural growth without performance degradation. However, it is constrained by architectural compatibility (e.g., activation functions) and primarily limited to functional knowledge transfer, not abstract or symbolic knowledge [62]. - AgentKB addresses cross-domain experience sharing for agentic problem-solving [33]. This framework abstracts concrete experiences into reusable patterns through variable generalization, step compression, and domain neutralization, balancing generality with specificity. A teacher-student dual-phase retrieval mechanism dynamically adapts knowledge, enabling effective transfer even between dissimilar domains [33]. The underlying assumption is that generalizable problem-solving strategies can be extracted from specific task executions. AgentKB’s strength is its ability to transfer experiential knowledge across diverse domains, leading to significant performance improvements across different difficulty levels and LLMs. Its primary limitation is the diminishing returns observed when applied to domains with minimal structural similarity, highlighting challenges in extreme Out-of-Distribution (OOD) generalization [33].
| The Information Bottleneck (IB) principle provides a theoretical lens for knowledge acquisition, focusing on learning maximally compressed yet informative representations. InfoBot applies this principle to multi-goal Reinforcement Learning (RL) to enhance transfer and exploration [56]. InfoBot learns policies that minimize the mutual information between the agent’s actions ($A$) and the goal ($G$) conditioned on the state ($S$), ($I(A;G | S)$), encouraging “default policies” and “goal-dependent modifications” only at “decision states” [56]. The policy $\pi_{\theta}(A | S,G)$ is parameterized by an encoder $p_\text{enc}(Z | S,G)$ and a decoder $p_\text{dec}(A | S,Z)$, where $Z$ is a latent variable representing goal information. A variational approximation $q(Z | S)$ and a modified reward term $\tilde{r}t \equiv r_t + \beta D{\text{KL}}(p_\text{enc}(Z | S,G) | q(Z | S))$ guide learning towards policies with strong transfer capabilities and effective exploration strategies [56]. While InfoBot offers robust transfer and exploration, its reliance on variational approximations and the sensitivity to the $\beta$ parameter represent practical challenges [56]. |
Another application of the Information Bottleneck principle is seen in Pluvio, which uses Conditional Variational Information Bottleneck (CVIB) for robust semantic representation learning in assembly clone search [24]. Pluvio leverages a large-scale pre-trained natural language model (all-mpnet-base-v2) and integrates CVIB to “compress the information learned about the code architecture and optimization settings” by treating them as nuisance information. This “forgets” domain-specific details, making representations invariant and enhancing generalization to unseen architectures and libraries. The CVIBEncoder, conditioned on architecture and optimization labels during training, disentangles instruction encodings from these factors [24]. Similarly, the IB-based skill learning in IBOL learns disentangled, interpretable, and robust skills by balancing informativeness and compression, alongside a “Linearizer” to abstract environment dynamics [35]. The Concept Bottleneck Layer (CBL) in CB-LLM also applies an IB-like approach to integrate interpretability into large language models by projecting embeddings into a concept space and disentangling concept information through adversarial training [32].
Deep Neural Network (DNN) extraction frameworks address the KAB by making implicit knowledge explicit and reusable, often through the creation of a substitute model. A framework for DNN extraction leverages public data and active learning to replicate the functional behavior of a secret model ($\tilde f \approx f$) [15]. The substitute model is trained using labels acquired from the secret model on samples selected via active learning, making implicit knowledge explicit through an input-output mapping. This framework demonstrates that while architectural compatibility between secret and substitute models leads to optimal “agreement” (e.g., 98.81% for BC-to-BC CNNs on MNIST), reasonable agreement can still be achieved with architectural mismatches (e.g., 97.21% for LC substitute) [15]. This highlights the transferability of functional knowledge across varied architectures. CEGA provides a similar model-centric framework for Graph Neural Network (GNN) extraction, iteratively refining a local replica by querying a target GNN [45]. These methods primarily achieve functional knowledge transfer, rather than deeper semantic or structural insights into the model’s internal mechanisms [15].
These solution frameworks aim to overcome critical challenges in knowledge acquisition, particularly the persistent knowledge acquisition and utilization gap in pre-trained models. Despite the inherent transfer learning capabilities of Large Language Models (LLMs) from vast text corpora [52], several limitations hinder their efficient knowledge utilization. Fine-tuning pre-trained LLMs for specific structured tasks, such as Knowledge Graph Completion (KGC), can sometimes degrade performance compared to training from scratch, indicating that generalized linguistic knowledge is not always optimally aligned with specialized domain requirements [49]. Furthermore, large_knowledge_model_perspectives_and_challenges highlights challenges such as “semantic loss” and “interference between textual and knowledge structural signals” in knowledge-injecting pre-training, and the “difficulty for acquisition” of intricate reasoning when relying on prompts. A critical assessment by revisiting_the_knowledge_injection_frameworks reveals persistent “Ineffective Knowledge Utilization” in knowledge-enhanced LLMs, where gains are often attributed to generic data augmentation rather than targeted knowledge integration. Moreover, zero-shot transfer of general-purpose NLP tools to highly specialized domains often yields significantly lower performance, indicating limitations in robustness and generalizability without further domain adaptation [48].
Synthesizing and comparing knowledge transfer approaches across domains reveals common strategies and domain-specific adaptations for efficient knowledge utilization:
- Pre-trained Language Models (PLMs) and LLMs: Many frameworks leverage the knowledge acquired during the extensive pre-training of LLMs like BERT, T5, Llama, and RoBERTa. This general linguistic and world knowledge is then transferred to downstream tasks through fine-tuning, parameter-efficient fine-tuning (PEFT) like LoRA [2,4,13,16,20,73], or prompting [40,43]. Domain-specific pre-training (e.g., SciBERT on scientific papers, BioBERT on biomedical texts) further refines this transfer, leading to superior performance in specialized information extraction tasks [2,18,25,51].
- Knowledge Graph (KG) Integration: KGs are a prime source of structured knowledge. Approaches include:
- KG Embeddings: Represent entities and relations in a continuous vector space, facilitating tasks like link prediction and knowledge base completion [9,74]. Uncertain KG Embeddings (UKGE) models extend this by integrating confidence scores, addressing the limitation of deterministic triples [55].
- KG-Enhanced Pre-training: Various methods inject KG knowledge into PLMs at the input, intermediate, or objective layers, or via structured/reStructured pre-training to integrate structural signals [7,12,42]. This helps models like ERNIE, LUKE, KnowBert, and K-BERT to fuse entity embeddings or use knowledge attention mechanisms [7]. Frameworks like
SAC-KGutilize fine-tuned T5 models as “Pruners” to guide KG growth by recognizing patterns in entity names, transferring knowledge about graph structure [66]. - Graph Reasoning with LLMs: Frameworks such as GRAIL fine-tune pre-trained LLMs for graph-specific reasoning using a two-stage training (SFT and RL) to transfer broad linguistic knowledge to graph retrieval tasks [63]. GraphGPT aligns LLMs with graph learning tasks via instruction tuning [71].
- Robotics: Transfer learning in robotics often involves pre-training vision models on large datasets like ImageNet to reduce data requirements for robot-specific tasks such as visual servoing [29,39,64]. Knowledge can also be transferred between robots or generalized across tasks using skill libraries, such as Dynamic Movement Primitives (DMPs) [64].
- Game AI: The AlphaZero framework demonstrates concept transfer by excavating sparse vector representations of dynamic concepts from its latent space and transferring them to both student AI agents and human experts [54]. This allows for the discovery of novel, machine-unique knowledge and its effective communication. Latplan transfers knowledge from subsymbolic sensor data to symbolic planning by learning compact latent representations and action models that can be compiled into PDDL, enabling the use of classical planners [28].
- Model Extraction and Distillation: Functional knowledge can be transferred from a secret model to a substitute model, even with architectural mismatches, via deep neural network extraction [15]. Diversity Induced Weighted Mutual Learning (DWML) facilitates knowledge transfer among student models through collaborative learning and knowledge distillation, often outperforming teacher-guided distillation on small datasets [8].
- Lifelong and Continual Learning: These paradigms focus on systems that continuously acquire new knowledge while retaining previously learned information. Techniques include architectural modifications (e.g., K-Adapter, LoRA, DEMix-DAPT, Lifelong-MoE) to preserve original parameters while adding new ones for task-specific knowledge, and meta-learning for intrinsic editability [20]. Analysis of “knowledge entropy decay” suggests that models at earlier pre-training stages are more plastic for continual learning, and artificial “resuscitation” of inactive memory vectors can improve knowledge acquisition and retention in later stages [34,69].
Despite significant advancements, limitations persist. The “knowledge circuit elasticity” in LLMs suggests a latent capacity for knowledge reactivation, but how to optimally leverage this for incremental learning remains an open question [34]. Challenges in knowledge integration include semantic loss when converting structured knowledge to textual form, potential interference between textual and structural signals, and the difficulty of acquiring precise knowledge through complex prompts [12]. The generalizability of transferred knowledge can be constrained by domain shifts and architectural mismatches [15,48]. Future research needs to focus on designing more robust and adaptive frameworks that can effectively handle these complexities, ensuring efficient and reliable knowledge acquisition across diverse domains and tasks. This includes developing mechanisms for disentangling relevant knowledge from noise, optimizing knowledge representation for seamless transfer, and advancing metacognitive capabilities to guide the learning process more intelligently.
4.5 Hybrid and Human-in-the-Loop Frameworks
Hybrid and human-in-the-loop (HIL) frameworks are pivotal in addressing the knowledge acquisition bottleneck (KAB) by strategically combining automated systems with human expertise. These approaches aim to balance the efficiency of automation with the precision, quality control, and nuanced judgment that human input provides [3,55]. The benefits of such frameworks include improved data quality, enhanced trustworthiness, and scalability through optimized resource allocation, particularly for complex or sensitive knowledge domains [4,48].
Human-in-the-Loop and Hybrid Strategies for KAB
| Strategy Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Active Learning (AL) | Iteratively selects most informative samples for human annotation. | Reduces manual effort, optimizes annotation budget, accelerates training. | Uncertainty sampling, PU-ADKA (expert selection), CEGA (graph sampling). | Computational cost of retraining, optimal acquisition function choice, initial data quality. |
| Expert Validation & Quality Control | Humans review/validate AI outputs, ensure correctness & quality. | Ensures accuracy, consistency, trustworthiness, particularly for KGs. | Manual verification, Bench4KE (human evaluation), DeepKE (custom schema), MatSKRAFT. | Resource constraints, time-consuming, human bias, scalability for large datasets. |
| Interactive Refinement & Steerability | Real-time feedback, direct guidance of AI models. | Improves model understanding, addresses errors, enhances user control. | TeachMe, MemPrompt (LLM correction), LBMs (textual summaries), CB-LLMs (concept intervention). | Human-AI discrepancy, potential for misguidance, computational overhead. |
| Human-Guided Data Generation | Humans initiate/guide data generation processes. | Bootstraps foundational knowledge, provides high-quality initial data. | Prompting LLMs for synthetic data, Agent KB (failure cases for LLM prompts). | Quality/bias of human input, cost of initial human effort. |
| Neuro-Symbolic Integration | Combines neural networks with symbolic reasoning/KGs. | Leverages human expertise implicitly, interpretability, robustness. | KNOW ontology, StructSense, LRNLP, Evo-DKD, KRDL. | Complexity of integration, architectural mismatch, consistency management. |
| Implicit Human Expertise | LLMs pre-trained on human-generated text embed common knowledge. | Reduces data scarcity, broad foundational understanding. | PLMs (BERT, GPT), human-curated KBs (Wikidata), DKA (prompt engineering). | Bias from training data, lack of provenance, not directly controllable. |
A systematic categorization of HIL strategies reveals diverse mechanisms for human involvement:
1. Active Learning for Efficient Annotation: This strategy focuses on reducing the manual effort and cost associated with data labeling by allowing the learning algorithm to intelligently query a human oracle for annotations on the most informative samples [6,57]. For instance, systems select samples based on uncertainty or similarity to prior errors, significantly minimizing the manual effort required to achieve high model performance under restricted budgets [25]. The PU-ADKA framework exemplifies cost-effective expert interaction in sensitive domains, optimizing knowledge acquisition within a fixed budget by considering expert availability, knowledge boundaries, and consultation costs [4]. This approach not only enhances domain-specific Large Language Models (LLMs) but also demonstrates the practical application of budget-aware resource allocation for human expertise.
2. Expert Validation and Quality Control: Humans are frequently integrated into systems for validating output, ensuring correctness, and maintaining data quality. This includes manual verification of facts in knowledge graphs (KGs), ontology creation and refinement, and benchmarking the performance of automated systems [3,48,55]. Examples include NELL’s use of user feedback to refine trustworthiness [55], the human evaluation of generated competency questions in Bench4KE’s gold standard dataset [14], and the human review processes in MatSKRAFT for materials knowledge extraction [65]. Similarly, DeepKE, while largely automated, facilitates human involvement through custom schema definitions and flexible usage guided by expert requirements [38]. The AXCELL system employs human-in-the-loop validation for semi-automatically extracting results from research papers, optimizing human effort by proposing top-ranked predictions [41].
3. Interactive Refinement and Steerability: More dynamic HIL strategies enable real-time feedback and direct steering of AI models. TeachMe and MemPrompt allow users to provide corrections, refining LLM knowledge and addressing factual errors or misunderstandings [20,75]. Language Bottleneck Models (LBMs) exemplify such steerability through: (1) prompt engineering the encoder to shape knowledge summaries; (2) reward signals from human preferences to enforce structural constraints; and (3) augmentation with student-specific information, allowing educators to edit summaries with additional insights [50]. The Concept Bottleneck LLM (CB-LLM) further allows users to intervene directly by deactivating neurons to remove biased elements or adjusting activations to steer generation away from harmful content, providing strong user control over model behavior [32].
4. Human-Guided Data Generation and Bootstrapping: Humans often initiate and guide data generation processes, providing the foundational knowledge for automated systems. This includes crafting prompts for LLMs to generate synthetic datasets [60,68] or defining initial rules and constraints for learning algorithms [72]. Agent KB uses manually annotated failure cases as few-shot examples to prompt LLM-based experience generation, demonstrating initial human input for bootstrapping knowledge [33].
Frameworks integrating diverse knowledge sources and semantic interoperability The “StructSense” framework highlights the emphasis on semantic interoperability and robust HIL evaluation [70]. It functions as a hybrid multi-agent system that combines the language capabilities of LLMs with agentic capabilities like tool use, memory, and iterative self-correction. Crucially, a feedback agent integrates human users, enabling them to provide natural language feedback or corrections prior to final output. While this HIL mechanism enhances reliability, it also increases operational cost and token usage, and its benefit may vary with model capability, demonstrating a clear trade-off between quality assurance and computational overhead [70].
The Multi-View Knowledge Model (MVKM) represents an advanced approach to integrating diverse learning resources [22]. MVKM models student interactions across both graded (e.g., quizzes) and non-graded (e.g., discussions) materials. Its architecture utilizes multi-view tensor factorization, decomposing interactions into a student latent feature matrix ($S$), a temporal dynamic knowledge tensor ($\mathbf{T}$), and concept-to-material mapping matrices ($Q^r$) for each resource type. The core mechanism lies in sharing $S$ and $\mathbf{T}$ across all material types, enabling knowledge transfer and a shared conceptual latent space. The model incorporates a flexible knowledge increase objective, penalizing knowledge loss while allowing for occasional forgetting, balancing reconstruction accuracy with this learning/forgetting constraint. Despite its sophisticated integration of diverse data, MVKM currently lacks explicit direct human-in-the-loop mechanisms for real-time feedback or refinement of the model itself [22].
Domain-Specific Adaptations of Human Involvement Human involvement differs significantly across domains, adapting to specific challenges and contexts:
- Robotics: Direct supervision often takes the form of Imitation Learning (also known as Programming by Demonstration, PbD), where humans physically demonstrate desired behaviors for robots to learn, reducing the need for extensive trial-and-error reinforcement learning [64]. This method is considered cost-effective as it allows non-experts to teach complex tasks. Hybrid approaches in robotics combine machine learning with classical control or planning, such as learning specific components of a behavior (e.g., perception or action) while relying on analytical models for others. Challenges remain in scaling human supervision and foreseeing human actions in complex Human-Robot Interaction (HRI) scenarios [64].
- Game AI: Human expertise is integrated for conceptual learning and validation, particularly in complex strategic games. A hybrid framework analyzing AlphaZero’s chess play discovered novel AI concepts and validated them through human studies involving grandmasters [54]. Grandmasters learned these AI concepts via prototype-based examples (chess positions) and improved their play, demonstrating successful knowledge transfer. This approach highlighted human-AI discrepancies such as prior biases and differing computational capacities, emphasizing the importance of understanding these gaps for optimized human-AI collaboration. While effective for games with discrete moves, prototype-based transfer may be less effective in domains lacking such clear structures [54].
- MLaaS (Machine Learning as a Service) / Adversarial Querying: Here, the “human-in-the-loop” concept shifts from a direct human annotator to an automated “oracle” (the target MLaaS model). Frameworks like CEGA use active sampling to iteratively query a target GNN model for informative nodes, aiming to reduce dependency on prohibitively expensive human labeling, especially in domains like biomedicine [45]. Similarly, in model extraction attacks, active learning strategies query a secret model to build a high-fidelity replica, optimizing query efficiency to minimize cost [15]. This contrasts with traditional HIL by replacing human judgment with an automated system, posing challenges for steerability and direct human feedback mechanisms.
Implicit Human Expertise Integration Beyond direct interaction, pretrained language models (PLMs) implicitly embed vast amounts of “human common knowledge” by training on extensive human-generated text data [24]. This broad understanding serves as a foundational form of indirect human expertise, mitigating data scarcity in specialized domains by pre-loading general human intelligence into the model. Frameworks like DKA and GRAIL leverage LLMs that encapsulate human-like knowledge and reasoning from their pretraining, using prompt engineering designed by humans to guide automated processes [61,63]. Furthermore, human-curated knowledge bases and ontologies, such as Wikidata, WordNet, or those defining schemas for KGs, provide structured forms of human expertise that guide automated systems, representing a static but crucial form of HIL design [3,7,36,74].
Blending Symbolic and Statistical Learning A significant hybrid approach involves the blending of symbolic (knowledge-based) and statistical (neural network) learning paradigms, often termed neuro-symbolic AI. This seeks to leverage the interpretability and reasoning capabilities of symbolic systems with the pattern recognition strengths of neural networks [29,47]. Knowledge-Rich Deep Learning (KRDL) integrates probabilistic logic with deep learning, using weak supervision strategies like data programming from expert rules [16]. C$^4$ agents employ a hybrid neuro-symbolic infrastructure to create trustworthy agents that can be instructed by humans and engage in lifelong learning through dialogue [58]. Latplan is another neuro-symbolic system that automatically generates symbolic planning models (PDDL) from raw visual input, bridging the gap between perception and reasoning and providing human-interpretable plans [28]. Modern approaches also combine LLMs with KGs, using the KG as an externally accessible tool for definitive answers and leveraging LLMs for coarse-grained reasoning or alignment with human preferences through frameworks like KnowPAT [12,52].
Limitations and Future Research
Despite the advancements, hybrid and HIL frameworks face several limitations. A primary concern is the resource constraint associated with human involvement; manual approaches are costly and time-consuming, and crowdsourcing can introduce quality issues due to non-uniform expertise [3,55]. Scalability remains a challenge for fully automated KG construction, as human intervention is still frequently necessary [3]. The computational cost and processing overhead of HIL can also be substantial, as seen in StructSense, where it increased operational cost and token usage [70]. Furthermore, human-AI discrepancy is a recurring issue, where LLMs may favor internal knowledge over provided context, or human biases and differing computational capacities can hinder optimal collaboration [20,54]. The lack of interpretability in some automated prompt generation methods, like AutoPrompt, can limit direct human oversight and refinement [43].
Future research needs to focus on several areas: (1) Optimizing interaction mechanisms to balance human effort and automated processes effectively, integrating dynamic human feedback for nuanced granularity differences and iterative refinement [55]. (2) Developing transparent and interpretable HIL systems that can justify decisions and foster trust, addressing the challenges of human oversight with opaque models [39]. (3) Designing robust architectures for human-LLM dialogue that can effectively manage knowledge conflicts, balance the benefits of natural language interaction with formal reasoning, and handle conflicting human inputs [12,52]. (4) Exploring mechanisms to guide powerful AIs with weaker human input and refine AI understanding when its capabilities may surpass human comprehension [12]. (5) Integrating metacognitive knowledge into AI systems, potentially requiring human-AI collaboration for defining and evaluating such aspects [26]. (6) Investigating how the principles of “social bootstrapping” and “shared latent codebook” can be computationally modeled for effective human-AI collaboration in knowledge acquisition and sharing tasks [46].
4.6 Cognitive and Neurosymbolic Approaches
Cognitive and neurosymbolic approaches represent a burgeoning research direction aimed at addressing the knowledge acquisition bottleneck (KAB) by integrating principles inspired by human cognition with AI system design. These approaches seek to enhance AI’s ability to acquire, represent, and reason with knowledge in ways that are more interpretable, adaptable, and robust, often by combining the strengths of neural networks with symbolic reasoning mechanisms.
A critical aspect within cognitive frameworks is the role of “meta characteristics” and explicit “metacognition,” which are hypothesized to enhance learning and adaptation by allowing systems to monitor and control their own cognitive processes. For instance, the concept of “meta-features as the representations of essential cognition” is proposed to enable AI to recognize distribution differences between known and unknown data, thereby guiding knowledge exploration in open-world scenarios [37]. However, this connection remains largely metaphorical, lacking concrete architectural details for computational modeling. In contrast, the content-centric computational cognitive (C$^{4}$) modeling framework explicitly positions “metacognition” as a necessary component for AI agents to emulate human behavior, integrating capabilities like introspection and mindreading [58]. This framework posits that metacognitive capabilities, including metaparameters such as confidence, vagueness, and actionability, support transparency, adaptability, and reasoning, moving towards human-legible explanations. Similarly, knowledge entropy within language models has been identified as a “meta characteristic” governing the balance between plasticity (ability to learn new knowledge) and stability (retention of old knowledge) [69]. The paper proposes a “resuscitation” method to increase knowledge entropy, artificially restoring plasticity in later-stage models, thus offering a mechanism to overcome knowledge transfer barriers in continual learning [69]. Further, the Self-Tuning framework, inspired by the Feynman Technique, incorporates “self-reflection” through closed-book generation tasks to foster systematic knowledge acquisition in LLMs [68]. The InfoBot architecture also reflects metacognitive principles through iterative refinement and self-correction, interpreting a KL-divergence term as a “cost of control” analogous to human cognitive effort [56]. While these approaches leverage cognitive insights to varying degrees, a common limitation is the abstract nature of their cognitive grounding or a lack of specific computational details for formalizing metacognitive parameters [37,58].
AlphaZero’s concept discovery framework exemplifies a cognitive approach for making black-box AI knowledge interpretable and transferable to human experts [54]. This framework operationalizes ‘concepts’ as concise, useful, and transferable “units of knowledge” linearly encoded in the latent space of AlphaZero’s neural network. A key contribution is the validation of concept teachability using Vygotsky’s Zone of Proximal Development (ZPD), hypothesizing that AI’s unique knowledge ($M-H$) lies within this zone, making it learnable by human experts with guidance [54]. This approach directly addresses the human-AI knowledge gap by aiming to expand human representational space ($H$) with AI-discovered insights. However, it largely bypasses the challenge of developing truly shared conceptual frameworks and does not delve into the detailed cognitive mechanisms of human concept internalization, nor does it propose specific cognitive models for human knowledge representation [54].
The Language Bottleneck Model (LBM) framework offers a solution for achieving interpretable knowledge tracing, directly addressing the KAB related to model opacity in educational settings [50]. LBM conceptualizes knowledge tracing as an inverse problem: instead of merely predicting student responses, it infers an “interpretable representation” of the student’s underlying knowledge state. Its theoretical foundation aligns with cognitive principles by recovering the latent knowledge state that explains observed behaviors, similar to how human educators infer conceptual understanding. The architectural choice of natural language as the bottleneck interface is pivotal, providing a flexible and interpretable medium for representing knowledge, misconceptions, and reasoning patterns, unlike fixed concept vocabularies. This allows LBMs to capture the “algorithmic essence of student behavior,” making the inferred knowledge states human-readable and actionable. A limitation of the LBM, however, is its reliance on an assumption of “quasi-static knowledge states,” which simplifies the dynamic nature of human learning, potentially leading to an architectural mismatch with continuous knowledge acquisition and forgetting processes [50].
Neurosymbolic Approaches for KAB
| Approach Category | Core Mechanism / Principle | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Metacognition | AI systems monitoring & controlling their own cognitive processes. | Enhanced learning, self-reflection, adaptability, human-legible explanations. | C^4 framework (metaparameters), Knowledge Entropy (resuscitation), Self-Tuning. | Often conceptual/metaphorical, lack concrete computational models, abstract grounding. |
| AlphaZero Concept Discovery | Extracts sparse, linearly encoded concepts from latent space. | Makes black-box AI knowledge interpretable & transferable to humans (M-H set). | Convex optimization, L1 norm, student AI teachability validation. | Limited to linear encoding, small sample size for human studies, methodological flaws possible. |
| Language Bottleneck Models (LBMs) | Natural language bottleneck for interpretable knowledge states. | Interpretable knowledge tracing, actionable insights for educators, steerability. | LLM encoder-decoder, GRPO for optimization. | Assumes “quasi-static knowledge states,” high computational cost, context length limits. |
| Explicit Control/Interaction | Direct integration of symbolic KBs/reasoning engines with neural nets. | Explainability, robustness, reduced catastrophic forgetting. | C^4 (hybrid infrastructure), LRNLP (symbolic goal, neural methods), Evo-DKD. | Technical specification for interplay, reliance on formal logic, scalability of reasoning. |
| KG-centric Neurosymbolic | KGs as structured, human-understandable symbolic layer. | Semantic grounding, interpretability, mitigation of hallucination. | StructSense (ontologies), KNOW (commonsense ontology), KG embeddings. | Hallucination risks for LLM-generated KGs, consistency with existing KGs. |
| Constraint-Driven/Logic-based | Embedding symbolic constraints or logical reasoning into neural models. | Ensures consistency, systematic generalization, adherence to domain expertise. | MatSKRAFT (GNNs with constraints), KRDL (probabilistic logic), NSI. | Integrating complex logic into neural architectures, scalability of constraints. |
| Symbol Grounding | Bridging symbolic and subsymbolic reasoning from raw input. | Generates symbolic problem representations from raw observations. | Latplan (State/Action Autoencoders, PDDL). | Symbol Stability Problem, uniform sampling issues, abstracting concepts. |
Neurosymbolic approaches, by combining neural (machine learning) components with symbolic manipulation (knowledge representation and reasoning formalisms), offer a powerful paradigm for overcoming specific limitations in knowledge acquisition, particularly related to explainability, robustness, and systematic generalization [59]. These architectures can be categorized by their integration mechanisms:
- Symbolic-Neural Hybrids with Explicit Control/Interaction: Some approaches directly integrate symbolic knowledge bases and reasoning engines with neural networks, often guided by cognitive analogies. The C$^{4}$ modeling framework, for example, utilizes a “hybrid, neurosymbolic infrastructure” that leverages symbolic representations (ontological models, lexicons) with neural processing (LLMs) to achieve metacognitive capabilities and maintain semantically interpretable knowledge resources [58]. Similarly, Logical Reasoning over Natural Language as Knowledge Representation (LRNLP) differentiates itself by having a typically symbolic goal while employing pure neural methods, thereby circumventing symbolic knowledge acquisition and scalability bottlenecks found in other neurosymbolic systems [75]. This design yields advantages such as interpretability and reduced catastrophic forgetting due to explicit knowledge bases. Evo-DKD represents a significant advancement in neuro-symbolic learning, tightly integrating symbolic ontology edits with neural natural language explanations via a dual-decoder design and a dynamic gating mechanism that acts as a “learnable mixture-of-experts” [17]. This architecture promotes a form of “self-reflection” by enforcing coherence between neural and symbolic reasoning streams.
- Knowledge Graph-centric Neurosymbolic Systems: Many neurosymbolic systems center around Knowledge Graphs (KGs) for their inherent symbolic representation and interpretability. KGs, rooted in semantic networks, provide a structured, human-understandable layer of knowledge [74]. Systems like
StructSenseincorporate domain-specific symbolic knowledge encoded in ontologies to guide LLMs, mitigating ambiguities and grounding outputs [70]. KNOW champions a neuro-symbolic approach by designing an ontology to capture “commonsense tacit knowledge” and “human universals” which LLMs can then manipulate, bridging neural representations with structured symbolic knowledge through “neuro-semantic synthesis” [36]. KG construction itself inherently involves neurosymbolic integration through ontology learning from text, KG embeddings (e.g., TransE, GraIL), deep learning for knowledge extraction, and rule-based data cleaning [3]. - Constraint-Driven and Logic-based Neurosymbolic Architectures: This category focuses on embedding symbolic constraints or logical reasoning into neural models. MatSKRAFT, for example, uses constraint-driven Graph Neural Networks (GNNs) that encode scientific principles directly into the model architecture, ensuring consistency and adherence to domain expertise [65]. The Knowledge-Rich Deep Learning (KRDL) framework combines probabilistic logic (symbolic) with deep learning (neural) using “weighted first-order logical formulas” to integrate explicit, structured knowledge with implicit, learned representations [16]. Historically, Neuro-Symbolic Integration (NSI) aimed to combine ANNs’ robust learning with symbolic logic’s explanatory power, evolving to include non-classical logics and probabilistic programming to address various forms of invariance and solve knowledge-based tasks [47].
- Symbol Grounding Approaches: Latplan is a pioneering neuro-symbolic system that bridges symbolic and subsymbolic reasoning by automatically generating symbolic problem representations from subsymbolic input. It uses a State Autoencoder (SAE) for grounding raw observations into propositional bit vectors and an Action Autoencoder (AAE) for learning action symbols, directly tackling the symbol stability problem with cognitive-inspired mechanisms [28].
Despite these advancements, several limitations and unaddressed questions persist. Many cognitive-inspired models remain largely conceptual or metaphorical, lacking concrete computational mechanisms for translating cognitive principles into AI architectures [37,64]. The “cognitive gap” between LLMs’ unorganized knowledge storage and humans’ associative thinking highlights a fundamental architectural mismatch that current models struggle to bridge, often relying on “reStructured pretraining” or integrating external KGs rather than intrinsically reorganizing knowledge [12]. The explicit integration of symbolic and neural reasoning, while a core tenet, often lacks detailed technical specifications regarding the interplay and control mechanisms between these components [58]. Furthermore, the assumption of linear encoding for concepts, while practical, may oversimplify complex cognitive phenomena [54]. The “Knowledge Soup” metaphor, while illustrative, underscores the current challenge of creating computational models that can fluidly manage diverse knowledge types, from solid structured chunks to flowing neural representations [12].
Future research should focus on operationalizing abstract cognitive principles into verifiable computational models. This includes developing more sophisticated mechanisms for metacognitive control and self-reflection in AI, moving beyond mere analogy to explicit integration into system architectures [26]. Investigating how knowledge entropy dynamically relates to human cognitive processes like selective attention or memory consolidation could inform more advanced cognitive architectures for LLMs [69]. Moreover, research is needed to determine how “intrinsic cognition” can be computationally modeled and verified, and which specific cognitive theories (e.g., developmental psychology) can inform the design of “meta-characteristics” and their interactions [37]. The precise computational methods for autonomously abstracting concepts from perceptual interactions and for seamlessly integrating traditional symbolic KBs with LLMs into a robust “Large World Model” remain critical open questions [12]. Ultimately, bridging the cognitive gap requires not just external knowledge injection but a fundamental shift towards AI systems that can intrinsically structure, reason about, and adapt their knowledge in a human-like, interpretable manner.
4.7 Reinforcement Learning and Exploration Frameworks
Reinforcement Learning (RL) frameworks offer a powerful paradigm for agents to acquire knowledge through active interaction with their environment, addressing the Knowledge Acquisition Bottleneck (KAB) by enabling efficient exploration, policy transfer, and intrinsic motivation. However, traditional RL methods often struggle with challenges such as sparse rewards, sample inefficiency, and the design of complex reward functions, leading to overfitting or task-agnostic exploration [28,64]. Contemporary research has advanced RL methodologies by incorporating sophisticated theoretical principles, modular architectures, and domain-specific adaptations to overcome these limitations.
| A prominent example of such advancement is the InfoBot framework, which fundamentally leverages the Information Bottleneck (IB) principle to tackle KABs in RL [56]. The IB principle, which aims to find a compressed representation of relevant information, regularizes goal-conditioned policies by minimizing mutual information between goals and actions. This regularization not only promotes generalization but also facilitates the learning of task-relevant structures [56]. Architecturally, InfoBot employs an encoder-decoder structure, where an encoder ($p_\text{enc}(Z | S,G)$) learns a compact, goal-relevant latent representation $Z$, and a decoder ($p_\text{dec}(A | S,Z)$) uses this representation alongside the state $S$ to select actions. This design establishes a “latent goal representation” that is crucial for abstracting task information [56]. InfoBot introduces several mechanisms to foster knowledge transfer and exploration. It encourages the emergence of “default policies” ($\pi_0(A | S)$), which represent goal-agnostic behaviors applicable across various tasks, akin to automatic actions in cognitive science. Concurrently, it identifies “decision states” where the agent must rely on specific goal information, requiring a shift from automatic to controlled action selection [56]. For exploration, InfoBot ingeniously utilizes the KL divergence term, $D_{\text{KL}}(p_\text{enc}(Z | S,G) | q(Z | S))$, as an intrinsic reward. This bonus incentivizes the agent to actively seek out decision states, guiding exploration towards information-rich regions of the state space, and is further augmented by a count-based mechanism ($\frac{\beta}{\sqrt{c(S)}}$) to promote novelty seeking. This intrinsic motivation directly addresses the challenge of sparse reward environments, enabling effective learning without dense external feedback [56]. |
Another framework deeply rooted in the Information Bottleneck principle is IBOL (Unsupervised Skill Discovery with Bottleneck Option Learning), focusing on unsupervised skill discovery for efficient exploration and policy transfer [35]. IBOL optimizes a trade-off between maximizing information about goals from skill latents and compressing irrelevant information from state trajectories, formulated as a lower bound optimization similar to $\beta$-VAE. Its modular architecture includes a pre-trained “linearizer” ($\pi_{\text{env}}$) that simplifies environmental dynamics, acting as a knowledge transfer mechanism by amortizing the cost of learning basic state transitions across multiple skill discovery tasks [35]. A “sampling policy” ($\pi_{\text{sample}}$) encourages diverse trajectory generation, while a “trajectory encoder” ($\text{TrajEncoder}$) maps these trajectories to continuous skill latent variables. Finally, a “skill policy” ($\pi_{\text{option}}$) learns to imitate the sampling policy’s output given a skill latent, defining the discovered skill [35]. This joint optimization ensures diversity and discriminability of learned skills, which can significantly reduce the effective horizon for downstream tasks, aiding learning in sparse-reward settings. Compared to existing methods like VALOR or DIAYN that learn skills on raw environment dynamics, IBOL’s approach makes it easier to learn diverse skills in complex environments [35].
Beyond explicit Information Bottleneck applications, various RL frameworks and RL-inspired techniques have emerged to address specific KABs. In the context of Large Language Models (LLMs), R1-Searcher++ employs Reinforcement Learning for dynamic knowledge acquisition, built upon the stable REINFORCE++ algorithm, adapted for retrieval tasks [27]. It allows LLMs to autonomously decide between internal knowledge and external retrievers, crucial for efficient exploration of vast knowledge spaces. A specialized “group reward” incentivizes internal knowledge utilization and minimizes unnecessary external queries, demonstrating a 30% reduction in retrieval counts compared to its predecessors while maintaining higher performance on multi-hop QA tasks [27]. This framework also integrates an external knowledge memorization mechanism, facilitating knowledge transfer by enriching the agent’s internal state with retrieved information, thus reducing repeated external queries [27]. Similarly, GRAIL utilizes the Group Relative Policy Optimization (GRPO) algorithm for training an intelligent graph retrieval agent, enabling efficient, step-wise exploration of knowledge graphs [63]. GRAIL employs a two-stage training process, combining supervised fine-tuning with RL to learn complex graph exploration strategies, thus transferring reasoning abilities from LLMs to the graph domain. It tackles sparse rewards by adopting “process-level rewards” (PRM), providing granular credit assignment to early-stage actions, further enhanced by a “Shortest Path Refinement” procedure to eliminate exploration redundancy [63]. However, the application of PRMs to synthetic data can introduce noise and reward signal misalignment, necessitating refinement procedures [63].
In LLM knowledge management, frameworks like KnowMap mitigate the need for traditional RL by providing dynamic environmental and experiential knowledge to LLMs, facilitating more informed decision-making and efficient exploration by reducing trial-and-error learning [44]. Its continuous accumulation of task trajectories supports lifelong learning and policy transfer. The PU-ADKA framework incorporates a Multi-Agent Reinforcement Learning (MARL) module with a Double DQN architecture to efficiently select information and transfer policies to LLMs under budget constraints [4]. Its reward function promotes collaborative and cost-efficient selection of diverse, high-impact questions, employing multi-agent competition and bootstrap sampling for generalization [4]. However, the computational cost associated with training and coordinating multiple agents limits extensive experimentation with varying agent numbers [4].
RL is also instrumental in broader contexts, such as robotics, where it is used for behavior acquisition requiring dynamic adaptation in uncertain environments [64]. Techniques like policy search (e.g., NAC, PoWER) and hierarchical RL enable robots to learn complex motor skills and goal-directed behaviors, often addressing implicitly sparse rewards through careful reward function design [64]. Despite its utility, RL in robotics faces significant challenges: sample inefficiency (requiring vast amounts of data), susceptibility to “reward hacking,” and the “reality gap” between simulation and real-world deployment [64]. Furthermore, in specialized applications, RL agents are designed for targeted tasks, such as PLUVIO’s Removal module, which uses a one-step RL game for pruning tokens in assembly functions to manage sequence length limits, optimizing a specific downstream utility rather than broad exploration [24]. Similarly, in the context of knowledge tracing, the Language Bottleneck Model (LBM) utilizes GRPO to train an encoder that generates interpretable summaries, optimizing a complex reward function that balances reconstruction accuracy, predictive accuracy, summary length, and structural constraints [50]. This process, however, is computationally costly due to iterative candidate summary generation and evaluation [50].
The application of RL to align LLMs with human values and instructions, through methods like RLHF and DPO, represents another significant domain. However, these applications typically focus on fine-tuning for alignment rather than addressing general KABs related to efficient exploration or policy transfer in diverse environments [5,12,30]. Methods like AlphaZero in game playing, while not primarily focused on efficient exploration during training, demonstrate how RL can lead to super-human knowledge acquisition and enable post-hoc discovery and transfer of unique concepts by leveraging MCTS statistics and policy-value network latent spaces [54]. The “teachability” of these discovered concepts to student networks highlights the transferability of learned knowledge within RL domains, despite limitations in generalizing to sparse rewards or inefficient exploration during the initial training phase [54].
Despite the diverse applications, several core challenges persist. The computational cost remains a significant barrier for complex RL systems [4,50,64]. The complexity of designing effective reward functions is also a perpetual issue, often leading to reward hacking or misaligned objectives [64]. Furthermore, while the concept of metalearning suggests learning algorithms that improve their own learning dynamics over time, its explicit application to efficient RL exploration strategies is still an area of active research [26]. Future research should focus on integrating symbolic representations into RL to enhance sample efficiency and interpretability, as suggested by studies exploring finite state machine representations and temporal logics for restraining policies [29]. Developing more robust and generalizable intrinsic motivation mechanisms, akin to InfoBot’s KL divergence bonus, is crucial for addressing sparse reward environments effectively. Advancements in modular architectures, leveraging pre-trained components or frozen encoders as seen in IBOL, hold promise for fostering knowledge reuse and reducing redundant learning, thereby further mitigating the knowledge acquisition bottleneck in diverse RL applications. Moreover, exploring how classical planning’s strengths in knowledge representation and solution optimality could inform RL exploration, rather than contrasting them, presents a valuable avenue for future inquiry [28]. Addressing the aforementioned limitations and actively exploring these research directions will be pivotal in enhancing the capabilities of RL frameworks for dynamic and efficient knowledge acquisition.
4.8 Adversarial Knowledge Acquisition Frameworks
Adversarial Knowledge Acquisition: Offensive vs. Defensive
| Aspect | Offensive: Model Extraction Attacks (MEA) | Defensive: MLaaS & LLM Security Strategies |
|---|---|---|
| Core Goal | Replicate a proprietary ML model (functional knowledge). | Protect ML models/data confidentiality, integrity, & IP. |
| Target | MLaaS models (DNNs, GNNs) as black-box oracles. | LLMs, MLaaS platforms, sensitive data. |
| Adversary’s KAB | Lack of secret training data, Limited query budget. | Securing against unauthorized access/replication, data exfiltration. |
| Provider’s KAB (Defensive) | Designing robust protection against sophisticated extraction. | Balancing security with usability/performance. |
| Key Techniques (Offensive) | Active Learning (Uncertainty, K-center, Adversarial), Universal Thief Datasets (ImageNet, WikiText-2). | On-premises LLMs, Secure RAG, Sandboxing, Data Anonymization, Encryption, Access Control, Red-Teaming. |
| Metrics (Offensive) | Agreement score, Fidelity, Accuracy, F1-score (under query budget). | Robustness against MEAs, Data privacy, Audit logs. |
| Ethical/Legal Implications | IP infringement, Copyright/Patent violations, Unauthorized redistribution, Privacy vulnerabilities. | Data privacy issues, Vulnerabilities from LLM-generated outputs, Responsible deployment. |
| Example Tools (Offensive) | [15] DNN Extraction Framework, CEGA (GNN Extraction). | [30] LLM Internal Security (Unlearning, Editing), [48] Secure Deployment Framework. |
| Binary Code Analysis (Related) | Pluvio: Extracts invariant semantics for clone search (can be used for IP infringement detection or vulnerability finding). | Protects IP in codebases, identifies vulnerabilities. |
Adversarial knowledge acquisition frameworks are characterized by their objective to extract or replicate proprietary intellectual property, such as machine learning models, from black-box oracles, often against the will of the model owner. This contrasts sharply with constructive knowledge acquisition, which focuses on legitimate data gathering and model development. The primary objectives of these adversarial frameworks include model replication, which can lead to intellectual property (IP) theft, copyright violations, or the development of surrogate models for further attacks or commercial exploitation [15,45].
A prominent architectural approach for adversarial knowledge acquisition in Machine Learning as a Service (MLaaS) environments involves query-based model extraction. One such framework, designed to extract Deep Neural Networks (DNNs), employs an iterative training mechanism to replicate the functionality of a secret model ($f$) into a substitute model ($\tilde{f}$) through black-box API queries [15]. The underlying assumption is that an adversary can query the target model with arbitrary inputs, though this might not always hold true in heavily protected MLaaS environments. This framework leverages two key components: Universal Thief Datasets and Active Learning Strategies. Universal Thief Datasets, such as large, diverse public datasets (e.g., ImageNet for images, WikiText-2 for text), serve as a source of unlabeled data. Their theoretical foundation lies in providing a “natural prior” that aids in overcoming the adversary’s lack of specific domain knowledge about the secret training data, proving more effective than uniform noise inputs [15].
The role of active learning is central to achieving query efficiency and optimizing model fidelity in adversarial knowledge acquisition [15]. In the DNN extraction framework, pool-based active learning strategies, including Uncertainty, K-center, Adversarial (DFAL), and an ensemble approach (Adversarial+K-center), are employed to minimize query costs by selecting the most informative samples from the universal thief dataset [15]. The process iteratively refines the substitute model: initial random queries label a small set of samples, then the current substitute model guides the active learning strategy to identify the most informative subsequent samples from the thief dataset. These are queried from the secret model, and their true labels are used to retrain a more accurate substitute model [15]. This approach demonstrates a significant trade-off advantage, achieving an average improvement of 4.70x for image tasks and 2.11x for text tasks in agreement between the secret and substitute models within a 30K query budget, significantly outperforming uniform noise baselines [15]. While highly effective for classification tasks, a limitation of this framework is its primary focus on classification, potentially limiting its applicability to other DNN types like generative models [15].
Another adversarial framework, CEGA, extends model extraction to Graph Neural Networks (GNNs) deployed as MLaaS, also operating without prior domain knowledge about the secret training data [45]. CEGA’s architectural choice emphasizes an active sampling strategy that selects informative nodes based on representativeness, uncertainty, and diversity criteria. This meticulous selection process is crucial for minimizing queries to MLaaS services, thereby reducing operational costs and avoiding detection through security alerts [45]. The success of CEGA highlights the adaptability of active learning to specific data structures, such as graphs, for efficient knowledge acquisition under stringent budget constraints. Its objective explicitly aligns with enabling malicious purposes, including copyright violations and IP infringement, by constructing high-fidelity replicas of proprietary GNNs [45]. A comparative weakness is that CEGA does not explicitly detail the use of “universal thief datasets” in the same manner as the DNN extraction framework, although its active sampling mechanism implies a similar function of selecting from an available data pool [45].
In contrast to these offensive adversarial knowledge acquisition frameworks, a distinct area of research focuses on defensive mechanisms against such threats. Papers like [30,48] do not propose adversarial acquisition techniques but rather concentrate on safeguarding AI systems, particularly Large Language Models (LLMs), from unauthorized access or misuse. Their objectives revolve around secure deployment and ensuring trustworthiness. Architectural choices and strategies include deploying on-premises LLMs, implementing Secure Retrieval Augmented Generation (RAG), sandboxing operations, data anonymization, PII scrubbing, differential privacy, access control, encryption, logging, and red-teaming [48]. Furthermore, intrinsic architectural designs, machine unlearning to forget sensitive information, and knowledge/representation editing to control harmful outputs are proposed to enhance trustworthiness and prevent malicious applications like “jailbreaking” or “toxic content generation” [30]. These defensive frameworks operate on the fundamental assumption that sensitive AI models and data require robust protection against various adversarial vectors, addressing risks such as LLM training data privacy and insecure user prompts [48]. The critical distinction is that these works evaluate existing tools for trustworthiness against adversarial scenarios, rather than providing methodologies for adversarial knowledge acquisition [30,48].
Limitations and Future Research: Despite the demonstrated effectiveness of adversarial knowledge acquisition frameworks, several limitations persist. The assumption of an adversary’s ability to choose any input for querying may not always hold in evolving MLaaS environments, which increasingly implement countermeasures like query perturbation, rate limiting, or restricted input domains [15]. Future research should investigate more sophisticated active learning strategies that can operate effectively under stricter query constraints or with partial observation capabilities. Furthermore, current frameworks primarily focus on classification tasks, leaving a gap for robust extraction methodologies for other complex DNN architectures, such as generative models or reinforcement learning agents [15].
An unaddressed question in existing work concerns the robustness of the extracted models to adversarial examples themselves, or how easily these extracted models could be subsequently used for other malicious purposes beyond simple replication [15]. This highlights the need for a comprehensive understanding of the lifecycle of an extracted model, from acquisition to potential misuse. Bridging the gap between effective acquisition and robust defense remains a critical area. Future work should explore more dynamic and adaptive defense mechanisms that can learn and counter novel acquisition techniques, while offensive research could focus on developing cross-domain extraction methods that are less reliant on specific data types or model architectures. The trade-off between query efficiency and model fidelity in active learning also warrants further investigation, particularly in scenarios where query budgets are extremely tight or where the cost of a mislabeled query is high.
5. Algorithmic Approaches and Techniques
Overcoming the knowledge acquisition bottleneck fundamentally relies on a diverse array of sophisticated algorithmic approaches and techniques.
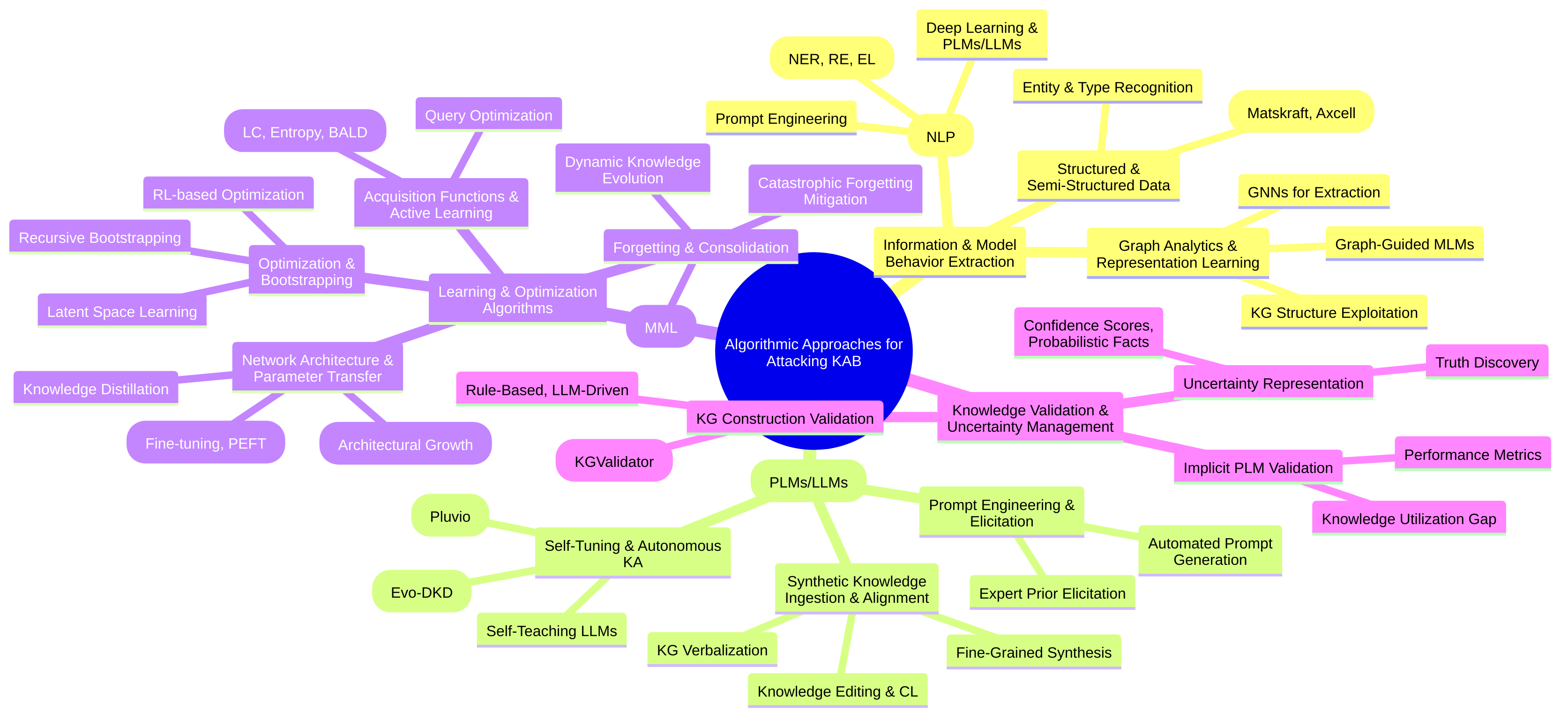
This section systematically delineates the primary methodologies employed to efficiently extract, synthesize, refine, and validate knowledge from heterogeneous sources and within complex artificial intelligence models. The landscape of these algorithms spans from traditional rule-based and statistical methods to advanced deep learning paradigms, large language models (LLMs), and graph-centric computations, all striving to transform raw data and implicit model states into actionable, structured knowledge [3,9,15].
The algorithmic approaches can be broadly categorized into two main paradigms. The first focuses on extracting explicit information from various data sources. This encompasses Natural Language Processing (NLP) techniques, which have evolved from rule-based and statistical models (e.g., Hidden Markov Models, Conditional Random Fields) for tasks like Named Entity Recognition (NER) and Relation Extraction (RE) to advanced deep learning architectures (RNNs, CNNs, Transformers) and pre-trained/large language models (PLMs/LLMs) like BERT and T5 [9,23,38]. These modern NLP methods leverage contextualized embeddings and prompt engineering to extract structured insights from unstructured text, even adapting to non-natural language data like assembly code [24]. Complementary to this are techniques for structured and semi-structured data extraction, which involve specialized algorithms to parse and interpret formats like scientific tables and logs. Frameworks such as Matskraft utilize Graph Neural Networks (GNNs) and constraint-driven learning for materials science tables, while Axcell employs structural information from LaTeX and contextual NLP to extract results from machine learning papers, highlighting the critical interplay of structural analysis, machine learning, and domain-specific rules [41,65]. Furthermore, graph analytics and graph-guided representation learning leverage the intrinsic structural properties of Knowledge Graphs (KGs) to enhance acquisition and inference. Algorithms like PageRank and GNNs are used for node importance and diversity in graph sampling (e.g., CEGA), while graph-guided representation learning in Masked Language Models (MLMs) integrates KG structures to enhance text understanding, supporting tasks like relation extraction, type completion, and Retrieval-Augmented Generation (RAG) systems [42,45,71].
The second paradigm shifts focus to model behavior extraction and replication, aiming to understand and manipulate the implicit knowledge residing within AI systems [15]. This includes techniques for black-box replication, where substitute models mimic the input-output behavior of a target model using active learning strategies and query optimization (e.g., Uncertainty, K-center, Adversarial approaches) [15,45]. More introspectively, internal model behavior extraction aims for interpretability and knowledge understanding, encompassing methods like knowledge localization and editing (e.g., Knowledge Neurons, ROME for LLMs), intervention-based methods (e.g., causal tracing, Edge Attribution Patching), probing (e.g., P-Probing for LLM hidden states), feature attribution, concept discovery (e.g., in AlphaZero), and uncertainty quantification [20,30,54,73]. Additionally, knowledge distillation techniques transfer functional knowledge from larger teacher models to smaller student models for efficient behavior replication [8].
Specifically for PLMs and LLMs, algorithms have evolved to facilitate knowledge acquisition and refinement through prompt engineering and automated knowledge elicitation. This has progressed from manual prompt design to automated methods like AutoPrompt, which use gradient-guided search to optimize trigger tokens for eliciting specific knowledge, effectively turning LLMs into active knowledge acquisition agents [43]. The efficacy of these methods hinges on carefully designed prompting, sometimes involving complex reasoning chains (e.g., Chain-of-Thought) or explicit prior elicitation (e.g., AutoElicit) to structure LLM outputs [12,19]. Furthermore, synthetic knowledge ingestion and knowledge alignment techniques proactively generate and integrate new knowledge into LLMs. This includes KG verbalization (e.g., TeKGen transforming Wikidata into KeLM corpus) and fine-grained synthesis (e.g., Ski generating QA pairs) to create formats digestible by LLMs [1,5]. Knowledge alignment, whether implicit (e.g., knowledge-injecting pre-training, knowledge editing, continual learning) or explicit (e.g., RAG, StructSense for contextual grounding), ensures consistency and coherence across diverse information sources [12,20,70]. The ultimate goal is self-tuning and autonomous knowledge extraction, where models can “self-teach” (e.g., Self-Tuning framework), autonomously decide between internal and external knowledge (e.g., R1-Searcher++), and even evolve ontologies (e.g., Evo-DKD) without continuous human intervention [17,27,68].
Underpinning these advanced capabilities are specialized learning and optimization algorithms. To overcome data scarcity, acquisition functions and uncertainty estimation (active learning) strategically select the most informative samples for labeling or querying. Techniques like Least Confidence, Entropy, and Bayesian Active Learning by Disagreement (BALD) quantify a model’s uncertainty to guide data acquisition, ensuring efficiency and reducing annotation costs [15,57]. Optimization and bootstrapping algorithms are crucial for iterative refinement and knowledge generation. This includes recursive bootstrapping (e.g., for entropy minimization in Optimal Transport), convex optimization for concept discovery (e.g., in AlphaZero), and bi-level optimization for dynamic student weighting in knowledge sharing [8,46,54]. Reinforcement learning (e.g., GRPO, REINFORCE++) is also employed for policy optimization in tasks like semantic token pruning (Pluvio) and dynamic knowledge acquisition (R1-Searcher++) [24,27,63]. Network architecture and parameter transfer techniques accelerate learning by leveraging existing knowledge. This includes Net2Net for dynamic architectural growth and knowledge transfer, transfer learning via fine-tuning PLMs, Parameter-Efficient Fine-Tuning (PEFT) methods (LoRA, Adapters), and knowledge distillation, often integrated with methods like Conditional Variational Information Bottleneck (CVIB) for domain-invariant representations [8,24,62,73]. Finally, forgetting and consolidation algorithms are essential for managing the stability-plasticity dilemma in incremental learning systems. These algorithms, informed by MML-derived metrics, govern what knowledge to retain, promote, or discard, preventing catastrophic forgetting in LLMs through data replay, regularization, or architectural modifications [20,67,69].
Crucially, knowledge validation and uncertainty management ensure the reliability and utility of acquired knowledge. This involves frameworks for automatic validation of KG construction, employing rule-based checks, semantic reasoning, and LLM-driven verifiers and pruners (e.g., KGValidator, SAC-KG, Evo-DKD) to ensure accuracy, consistency, and logical integrity [17,40,66]. Uncertainty management explicitly classifies and represents knowledge uncertainty (e.g., Invalidity, Vagueness, Timeliness) within KGs using confidence scores or probabilistic methods, with fusion algorithms inferring true values from conflicting claims [55]. In PLMs, validation is often implicit, measured by performance on downstream tasks or through explicit uncertainty estimation (e.g., AutoElicit for predictive uncertainty) [19,53]. Across domains, from the explicit consistency demands of KGs to the robustness requirements of robotics and the concept teachability in game AI, the approaches to validating and managing uncertainty are tailored to the specific operational contexts and forms of knowledge [54,64].
Collectively, these algorithmic approaches underscore a continuous effort to tackle the knowledge acquisition bottleneck. However, recurring challenges include the interpretability and reliability of knowledge representations (especially in black-box LLMs and GNNs, where concerns about hallucination persist), scalability and computational efficiency for massive datasets and large models, effectively managing uncertainty from diverse sources, and addressing issues like semantic loss during knowledge transformations and the continuous tension between generalizability and domain-specificity [12,43,55,72]. Future research will likely focus on developing more robust, adaptive, and explainable algorithms that seamlessly integrate information, foster lifelong learning, and establish trustworthy knowledge acquisition ecosystems.
5.1 Information and Model Behavior Extraction Algorithms
This section delves into the diverse algorithmic approaches designed to overcome the pervasive knowledge acquisition bottleneck, broadly categorizing them into two main paradigms: the extraction of explicit information from various data sources and the more introspective analysis of implicit knowledge and behavior within AI models themselves. The evolution of these techniques, from traditional rule-based and statistical methods to advanced deep learning, large language models (LLMs), and graph-centric algorithms, represents a continuous effort to efficiently transform raw data and complex model states into actionable, structured knowledge [3,9,15].
The first paradigm, information extraction from data, focuses on converting heterogeneous data inputs into structured representations, primarily for populating and enriching knowledge bases and graphs. This encompasses three distinct, yet often complementary, sub-areas:
-
Natural Language Processing (NLP) Techniques for Extraction: This subsection explores the progression of NLP methodologies, foundational for transforming unstructured textual data into structured insights. It begins with traditional preprocessing steps and core information extraction (IE) tasks such as Named Entity Recognition (NER), Relation Extraction (RE), and Entity Linking (EL), which historically relied on dictionary lookups, rule-based systems, or statistical models like Hidden Markov Models (HMMs) and Conditional Random Fields (CRFs) [3,9]. The narrative then shifts to the transformative impact of deep learning, particularly recurrent neural networks (RNNs), convolutional neural networks (CNNs), and Transformer architectures, which have significantly minimized the need for manual feature engineering and enhanced scalability and pattern recognition. The advent of pre-trained language models (PLMs) and LLMs like BERT and T5 is highlighted, showcasing their capability to handle complex IE tasks by leveraging contextualized embeddings and framing extraction as sequence-to-sequence problems, often guided by sophisticated prompt engineering strategies [23,38,43,66]. The application of these techniques extends to specialized domains like scientific literature and even non-natural language data such as assembly code, underscoring their versatility [2,24].
-
Structured and Semi-Structured Data Extraction: This area addresses the specialized challenges of extracting knowledge from data formats that possess inherent structural cues, such as scientific tables, logs, and encyclopedic resources. Unlike unstructured text, these sources require algorithms that can parse and interpret complex layouts and domain-specific semantics to maximize precision and reliability [41,65]. This subsection features frameworks like
Matskraft, which employs Graph Neural Networks (GNNs) and constraint-driven learning for materials science tables, andAxcell, which leverages LaTeX structural information, ULMFiT-based classifiers, and contextual NLP for automated results extraction from machine learning papers. The discussion emphasizes the critical interplay between structural analysis, machine learning models, and domain-specific rules for effective knowledge acquisition from these heterogeneous sources, while also touching upon entity and type recognition algorithms for refining knowledge graph schemas [31,41,65]. -
Graph Analytics and Graph-guided Representation Learning: This subsection focuses on leveraging the intrinsic structural properties of information, particularly within Knowledge Graphs (KGs), to enhance knowledge acquisition and inference. It explores how KGs represent entities and relationships as nodes and edges, facilitating sophisticated query languages and rule systems for knowledge inference and completion [3,29]. The content covers algorithmic steps for graph-based model extraction and acquisition, such as CEGA’s use of PageRank and GNNs for node importance and diversity in sampling, and methods for exploiting structured knowledge in text via graph-guided representation learning in Masked Language Models (MLMs) [42,45]. Various graph-based approaches, including Heterogeneous Information Networks (HINs), Knowledge Graph Embeddings (KGEs), and Graph Neural Networks (GNNs), are discussed for tasks like relation extraction, type completion, and Retrieval-Augmented Generation (RAG) systems [63,71,72,74]. It also critically examines scenarios where graph-guided methods are strategically avoided due to noise or integration complexities, highlighting the trade-offs involved [24,40].
The second paradigm focuses on model behavior extraction and replication, moving beyond data to understand and manipulate the knowledge residing within AI systems. This distinct area explores techniques that aim to reveal the implicit logic, decision boundaries, internal representations, and functional mechanisms inherent in trained models [15]. This paradigm includes:
- Model Behavior Extraction and Replication Algorithms: This subsection explores methods for analyzing, understanding, and transferring the capabilities of AI models. It distinguishes between black-box replication, where substitute models are trained to mimic the input-output behavior of a target model using active learning strategies and query optimization (e.g., Uncertainty, K-center, Adversarial approaches for DNNs, and CEGA for GNNs) [15,45]. It then delves into internal model behavior extraction for interpretability and knowledge understanding, covering techniques like knowledge localization and editing (e.g., Knowledge Neurons, ROME for LLMs), intervention-based methods (e.g., causal tracing, Edge Attribution Patching for circuit discovery), probing (e.g., P-Probing, Q-Probing for LLM hidden states), feature attribution, concept discovery in complex AI systems like AlphaZero, and uncertainty quantification [20,25,30,54,73]. Finally, knowledge distillation techniques are discussed, which transfer functional knowledge from larger teacher models to smaller student models to replicate behavior efficiently [8]. The section also outlines general model behavior analysis methods, including memorization studies, the Knowledge Acquisition Utilization (KAU) gap framework, and the evaluation of domain generalizability [48,53,60].
Collectively, these sub-sections highlight the sophisticated algorithmic landscape for knowledge acquisition. A critical overarching theme across all areas is the continuous tension between generalizability and domain-specificity, with general-purpose LLMs offering broad applicability but often requiring fine-tuning or careful prompting for domain-specific precision, while specialized models excel in narrow contexts but lack wider adaptability [48]. Recurring challenges include the interpretability and reliability of knowledge representations, particularly in complex black-box models like LLMs and GNNs, where concerns about factual accuracy, “hallucination,” and the verifiability of causal links persist [12,43,54]. Scalability and computational efficiency remain significant hurdles, especially when dealing with massive datasets, very large KGs, or the training and deployment of large models [9,72]. Furthermore, effectively managing uncertainty in extracted knowledge from diverse sources and addressing semantic loss when transforming structured information (e.g., KGs) into textual formats for LLM processing are key areas for future research [12,55]. Future directions will likely involve developing more robust, adaptive, and explainable algorithms that seamlessly integrate information from disparate sources and internal model states, moving towards a more comprehensive and trustworthy knowledge acquisition ecosystem.
5.1.1 Natural Language Processing (NLP) Techniques for Extraction
Natural Language Processing (NLP) techniques are fundamental to converting unstructured text into structured information, a crucial step in addressing the knowledge acquisition bottleneck. This conversion process forms the bedrock of information extraction (IE), which involves detecting phrases, identifying entities, and deriving relationships from natural language [9].
Fundamental NLP for information extraction begins with a series of preprocessing stages, including tokenization, stemming, part-of-speech (POS) tagging, and syntactic parsing (both constituency and dependency parsing). Tokenizers break down text into individual units, while stemmers and lemmatizers reduce words to their root forms, aiding in canonical representation [6,9]. POS taggers assign grammatical roles to words, and parsers analyze sentence structure, which is essential for understanding relationships and scope [6,9].
Core IE tasks built upon these foundations include Named Entity Recognition (NER), Relation Extraction (RE), Entity Linking (EL), Coreference Resolution (CR), and Event Extraction. NER identifies and classifies entities such as persons, organizations, and locations [3,9]. Early NER methods relied on dictionary lookups or statistical machine learning models like Hidden Markov Models (HMMs) and Conditional Random Fields (CRFs) with extensive feature engineering [3,9,72]. EL (also known as Wikification) links identified entities to entries in a knowledge base (KB), resolving ambiguity by considering local context and global coherence [9,72]. CR identifies different expressions that refer to the same real-world entity, crucial for understanding document-level information [9,48]. RE identifies semantic relationships between entities, forming structured triples (subject, relation, object) that populate knowledge graphs [9,55]. Traditional RE methods included rule-based patterns and feature-based statistical models, which suffered from limited recall and high human involvement in pattern design [3]. Semantic parsing, a more advanced NLP task, maps natural language text to formal meaning representations, often grounded in KBs for applications like question answering [72].
Modern approaches, particularly deep learning, have significantly enhanced these capabilities. The shift from traditional statistical models to deep neural networks (DNNs), especially Long Short-Term Memory (LSTM) networks, Convolutional Neural Networks (CNNs), and Transformer architectures, has propelled the state-of-the-art in IE tasks. Deep learning models minimize the need for manual feature engineering, improve scalability, and can identify more complex patterns. For instance, the DeepKE toolkit implements various IE tasks using deep learning models such as BERT, BART, CNNs, RNNs, Capsule networks, GCNs, and Transformers for NER, RE, and Attribute Extraction (AE) [38]. It also supports multimodal NLP by integrating textual and visual features with models like IFAformer [38]. Pre-trained language models (PLMs) like BERT and RoBERTa serve as powerful encoders, generating contextualized embeddings for sentences and entities, which are then fed into task-specific prediction layers [3,38].
The advent of Large Language Models (LLMs) has revolutionized information extraction by framing IE tasks as sequence-to-sequence problems, allowing models like T5 and BART to generate linearized representations of knowledge graph elements from raw text [23]. LLMs inherently possess strong language understanding and generation capabilities, making them adept at tasks such as verbalizing knowledge graph components into textual formats for generative KG completion [49]. Frameworks like SAC-KG leverage LLMs (e.g., ChatGPT, Qwen, Llama2) as core extractors, prompting them with instructions and in-context examples to elicit structured output like knowledge triples [66]. Similarly, StructSense uses LLMs (GPT-4o-mini, Claude 3.7 Sonnet) to convert raw natural language into structured JSON outputs based on task configurations [70].
A critical aspect of leveraging LLMs is prompt engineering, which has evolved from simple textual prompts to complex structures like Chain-of-Thought (CoT), Tree of Thoughts (ToT), and Graph of Thoughts (GoT) [12]. These advanced prompting techniques aim to guide LLMs to elicit specific knowledge and improve reasoning performance. Automated prompt generation methods, such as AutoPrompt, offer significant advantages over manual prompt engineering. AutoPrompt uses a gradient-guided search to find “trigger tokens” that, when combined with input, maximize the target task’s label likelihood, effectively reformulating tasks like sentiment analysis, NLI, fact retrieval, and relation extraction as fill-in-the-blank problems solvable by masked language models (MLMs) [43]. This automated approach overcomes the suboptimality of manual prompts and the laborious nature of high-quality prompt engineering [20,43]. Soft-prompting, which involves training continuous prompt embeddings, is another technique used to probe and extract existing parametric knowledge within PLMs for diagnostic purposes, allowing for zero-shot prediction of tail entities with enhanced consistency [53].
Fine-tuned NLP models are particularly effective in extracting knowledge from specific domains. For scientific texts, models like BART and LED are fine-tuned for summarization, while BERT, SciBERT, and SciDeBERTa are used for extractive and abstractive Question Answering (QA) and NER on scientific datasets [2]. Frameworks like SciNLP-KG employ BERT-based models (e.g., RoBERTa) for entity recognition and relation extraction, even for inter-sentence relations, from scientific papers [11]. MatSKRAFT uses MatSciBERT to obtain initial node embeddings from scientific tables, integrating contextual understanding of text within structured data [65]. In the biomedical domain, HYPE utilizes CNNs, RNNs, and TCNs with Word2Vec embeddings for detecting hypoglycemia events in electronic health records [21], while BioBERT and BiLSTM-CRF models are fine-tuned for mutation NER [25].
The evolution from traditional NLP methods to deep learning approaches has brought significant improvements in accuracy and scalability. Traditional methods, often rule-based or relying on extensive feature engineering, struggled with generalization and adaptation to new domains, requiring human intervention for pattern design or feature selection [3,55]. Deep learning models, especially Transformer-based PLMs, can capture more complex linguistic patterns and semantic nuances from vast amounts of unlabeled text, leading to higher performance across a wider range of tasks [3,52]. For example, the use of PLMs in relation extraction has pushed the state-of-the-art to new heights, often trained with distant supervision to overcome data scarcity [3]. However, this also introduces new challenges, such as the computational cost of training and deploying large models.
NLP techniques are also adapted for highly specialized textual domains beyond natural language. For instance, the all-mpnet-base-v2 sentence transformer, a PLM, has been applied to assembly code analysis by treating assembly instructions as text. This involves tokenization using MPNetTokenizer and generating embeddings via MPNetEmbedder, leveraging the model’s masked and permuted language modeling pre-training to capture semantic representations of the code [24]. This demonstrates the advantage of large-scale pre-training and transfer learning for extracting semantic understanding in data-scarce, non-natural language domains. Similarly, LSTMs have been used to learn low-dimensional embeddings of natural language instructions to guide Reinforcement Learning (RL) agents in instruction-following tasks, enabling agents to reason over instruction text and environment configurations [56]. LLMs can also encode student interaction histories into natural language summaries for interpretable knowledge tracing [50]. These adaptations highlight the versatility of modern NLP models in deriving meaning from diverse forms of textual data, even when the “text” is not traditional human language.
Despite significant advancements, several limitations and areas for improvement persist. A major challenge is the interpretability of LLM-generated prompts, which can often be ungrammatical and difficult for humans to understand, hindering insights into the model’s elicited knowledge [43]. The black-box nature of LLMs also reduces transparency in specific NLP sub-tasks compared to traditional pipelines [66]. Accuracy remains a concern, as LLMs can struggle with factual correctness, numerical facts, and long-tail entities, often performing less accurately than specialized, smaller models for certain IE tasks [12,55]. LLMs are also susceptible to “hallucination,” necessitating robust validation processes [52,61].
Scalability and generalizability also present ongoing challenges. LLMs have context length limitations that can hinder processing long documents or interaction histories [50]. While versatile, PLMs applied to non-natural language data like assembly code might miss unique low-level semantic and structural properties not easily captured by text models [24]. Furthermore, even state-of-the-art tools often exhibit limited generalizability to specialized domains in zero-shot settings, requiring domain-specific fine-tuning or careful adaptation [48]. For pipeline approaches, errors in earlier stages, such as initial entity tagging, can propagate and reduce overall system precision [11]. Future research should focus on enhancing LLM interpretability, improving factual accuracy and robustness, developing more efficient methods for handling long contexts, and minimizing “semantic loss” when converting structured knowledge graphs into textual representations for LLMs [12]. Investigating how knowledge entropy decay impacts specific NLP techniques within LLMs in continual learning contexts also presents an important research direction [69].
5.1.2 Graph Analytics and Graph-guided Representation Learning
Graph analytics and graph-guided representation learning are pivotal in addressing knowledge acquisition bottlenecks by leveraging the intrinsic structure of information. Knowledge Graphs (KGs), serving as structured repositories, inherently facilitate graph-based representation, where entities are nodes and relationships are edges, enabling sophisticated query languages and rule systems for knowledge inference and completion [3,29].
Graph Analytics and Graph-Guided Learning Techniques
| Technique Category | Core Mechanism | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| KG as Structured Representation | Nodes (entities), Edges (relations) organize knowledge. | Facilitates sophisticated query languages, rule systems for inference. | DBpedia, Wikidata, OWL, SPARQL. | Incompleteness, manual construction, consistency management. |
| Graph-based Model Extraction | GNNs & graph analytics for replicating target model behavior. | Cost-effective GNN acquisition under budget constraints. | CEGA (PageRank, GNNs, K-Means for representativeness/diversity). | Primarily functional transfer, not semantic insight, assumes query access. |
| Graph-Guided MLMs | Integrating KG structures to guide representation learning in MLMs. | Enhances text understanding, embeds relational knowledge implicitly. | GLM (KG-guided entity masking & distractor-suppressed ranking). | Dependency on predefined hyperparameters, limited robustness across diverse KGs. |
| Heterogeneous Information Networks (HINs) | Nodes & edges of distinct types capture complex relationships. | Derives rich features from meta-paths/meta-graphs. | Commuting matrices for text classification. | Scalability for very large graphs, computational cost of path enumeration. |
| Knowledge Graph Embeddings (KGEs) | Transforms entities & relations into low-dimensional vector spaces. | Preserves graph structure, enables link prediction & type completion. | TransE, TransH, TransR, UKGE (uncertainty integration). | Struggle with unseen entities, scalability issues for complex models. |
| Graph Neural Networks (GNNs) | Propagates information over graph structure. | Used for node classification, relation extraction, graph exploration. | DeepKE (GCNs for RE), MatSKRAFT (GATs for table processing), GRAIL (KG exploration). | Do not always outperform traditional algorithms, interference with textual signals. |
| Graph-based RAG | Uses KGs to retrieve & ground LLM responses. | Enhances factual accuracy, reasoning, transparency in LLMs. | Keqing, GRAG, MindMap, GLBK, GraphCoder (code context graphs). | Scalability for large KGs, processing speed, resource usage. |
| Selective Graph Avoidance | Deliberately avoids graph structures due to noise/complexity. | Mitigates noise from compilation artifacts in binary analysis. | Pluvio (forgoes CFGs for assembly code). | Potential loss of explicit topological information. |
The utility of these methods spans from enhancing language models to automating knowledge extraction and refining ontological structures.
One prominent application involves algorithmic steps for graph-based model extraction and acquisition. CEGA, for instance, employs a cost-effective approach for model acquisition that extensively utilizes graph analytics within its representativeness module [45]. It identifies candidate nodes by analyzing existing or assumed graph structures, relying on structural indices such as PageRank to quantify node importance. The PageRank score for a node $v$ in an acquired graph $\mathcal{G}{\mathrm{a}}$ is computed recursively as: \(\mathcal{L}_1^\gamma (v, \mathcal{G}_{\mathrm{a}}) = \frac{1 - \xi}{N} + \xi \sum_{w \in \mathrm{in}(v)} \frac{\mathcal{L}_1^\gamma (w, \mathcal{G}_{\mathrm{a}})}{L(w)}\) where $N = |\mathcal{V}{\mathrm{a}}|$ is the number of nodes, $\mathrm{in}(v)$ denotes nodes pointing to $v$, $L(w)$ is the number of outbound edges from $w$, and $\xi$ is a damping factor (typically 0.85) [45]. This calculation ensures that selected nodes encapsulate the graph’s structural essence. Furthermore, CEGA leverages Graph Neural Networks (GNNs) for node classification and applies K-Means clustering to node embeddings for diversity analysis, ensuring the acquired nodes represent varied structural patterns [45].
The utility of graph-based methods in knowledge acquisition is particularly evident in “exploiting structured knowledge in text via graph-guided representation learning” [42]. This approach integrates KG structures to guide representation learning in Masked Language Models (MLMs). For example, a KG-guided entity masking scheme selects informative entities for masking based on properties like document frequency ($\text{docfreq}$) and mutual reachability ($\text{neighbor}$), which measures the shortest undirected path length ($\text{gpath}$) between entities within a specified number of hops ($\text{R}_{\text{hop}}$) in the linked KG [42]. This heuristic-based guidance, while effective, introduces a dependency on predefined hyperparameters and may limit robustness across diverse KGs, pointing to a need for more adaptive, learned graph-processing models [42].
Different graph-based approaches exhibit varied strategies for knowledge representation and extraction. Heterogeneous Information Networks (HINs), for instance, represent world knowledge with distinct node and edge types, utilizing meta-paths and meta-graphs to derive features such as commuting matrices. These features capture complex relationships not discernible through simpler methods, significantly aiding tasks like text classification and clustering [72]. However, HINs can face scalability and computational cost challenges, especially for very large graphs and the enumeration of all path instances [72]. In contrast, Knowledge Graph Embeddings (KGEs), including models like TransE, TransH, and TransR, transform entities and relations into low-dimensional vector spaces, preserving graph structure and enabling link prediction and type completion [3,9,74]. While effective, many shallow embedding approaches struggle with unseen entities, necessitating inductive methods such as GNNs [3].
The importance and application of graph analytics and mining algorithms in overcoming knowledge acquisition bottlenecks within KGs are manifold. These algorithms infer new knowledge, identify inconsistencies, and suggest improvements to graph structures. Relation extraction, type completion, and holistic entity linking all benefit from graph-based methodologies that integrate known relations and leverage structural information [3]. DeepKE, for example, incorporates GCNs for relation extraction, utilizing graph structures like parse trees to improve classification by propagating information over grammatical dependencies [38]. MatSKRAFT transforms scientific tables into graph representations and employs Graph Attention Networks (GATs) for processing, integrating structural constraints to enhance knowledge extraction from semi-structured data [65]. For generative knowledge graph completion, models like “Better Together” leverage node neighborhood information, verbalizing 1-hop neighbors as contextual input to language models, demonstrating the explicit integration of graph context into representation learning [49].
Knowledge Graphs (KGs) offer significant advantages as a framework for structured knowledge acquisition and representation due to their explicit encoding of relationships, which is crucial for verifiable and traceable intelligence [48]. GNNs are increasingly trained and utilized for interaction within KGs, as exemplified by frameworks like GRAIL [63]. GRAIL defines specific graph exploration algorithms, such as $\text{Explore}(x)$, which systematically examines relation-centric contexts around an entity $x$, returning the complete set of associated triples. A pruning algorithm, $\text{Choose}(q,\mathcal G^{\text{p}})$, then distills a relevant subgraph $\mathcal{G}^{sub}$ based on a query $q$ and a binary classifier $F$, which determines the relevance of each relation. This iterative process allows LLM-based agents to interact with large KGs for retrieval-augmented reasoning [63]. Furthermore, graph-based RAG systems utilize a range of graph algorithms including shortest path algorithms (e.g., in GLBK, GNN-RAG), probabilistic methods like Personalized PageRank (HippoRAG) and random walks (WalkLM), and heuristic-based K-hop sampling (HybridRAG, GRAG) to enhance retrieval accuracy and provide transparent reasoning [71]. Learning-based approaches within RAG commonly employ GNNs (KG-FiD, REANO, EtD, QA-GNN) and attention mechanisms (ATLANTIC, HSGE, HamQA) to propagate information and update entity representations, while contrastive learning (SURGE) aids in maintaining consistency with generated responses [71]. Community detection algorithms (GraphRAG) are also used to group related entities for efficient multi-hop reasoning, showing the breadth of graph analytics in modern knowledge systems [71]. Beyond the neural approaches, symbolic systems also harness graph analytics; for instance, in incremental knowledge acquisition, a coverage graph represents deductive relationships between rules, with a hierarchical support metric ($\text{SupC}$) propagated recursively to assess rule utility and guide consolidation processes [67].
Despite the pervasive utility of graph-based methods, researchers sometimes strategically choose to avoid them, particularly when facing specific knowledge acquisition challenges. Pluvio, for instance, forgoes graph-guided representation learning based on Control-Flow Graphs (CFGs) for assembly clone search [24]. The underlying assumption is that CFGs, while rich in structural information, introduce noise due to compiler optimizations and intricate intra-instruction structures. By focusing on tokens from assembly instructions instead, Pluvio aims to mitigate this noise and improve generalization across out-of-domain architectures and libraries, demonstrating a trade-off where structural abstraction is sacrificed for robustness in a noisy domain [24]. Other contexts, such as KGValidator and some knowledge injection frameworks, treat KG information as textual content for LLMs, effectively bypassing direct graph traversal or reasoning in favor of simplified integration or processing efficiency [7,40]. This choice often stems from the practical ease of processing structured knowledge within existing LLM pipelines rather than developing complex graph-native integration methods, despite the potential loss of explicit topological information. Similarly, LLM-based logical reasoning systems may opt to avoid symbolic representations, including KGs, in favor of direct natural language processing, as seen in LRNLP [75].
Critically, while graph-aware large models are advancing, they often do not outperform traditional specialized graph algorithms in tasks inherently reliant on structured knowledge like link prediction, association graph mining, or subgraph analysis [12]. This performance gap suggests limitations in how current large models fully leverage complex graph structures. Intermediate-layer injection of KG embeddings can also suffer from interference between textual semantic signals and knowledge structure signals, leading to suboptimal integration [12]. Moreover, the scalability and computational cost remain significant challenges for graph analytics on very large and dynamic KGs, particularly for approaches relying on feature engineering from HINs or complex probabilistic models [9,72]. Future research needs to focus on designing GNN-based or Transformer-based models that consistently surpass traditional graph algorithms for all structured tasks, integrating more sophisticated graph analytics for nuanced uncertainty management, and addressing the data scarcity and architectural mismatch challenges in developing standardized graph analytics for domain-specific KGs [3,48,55]. Novel methods should aim to learn more robust and adaptive graph-guided representations that can generalize across diverse structural properties of KGs and overcome the existing knowledge complexity mismatch when integrating with LLMs [7].
5.1.3 Structured and Semi-Structured Data Extraction
The acquisition of knowledge from structured and semi-structured data sources presents distinct challenges compared to extracting information from free-form text, necessitating specialized frameworks and algorithms. These sources, such as scientific tables, encyclopedic resources, and logs, possess inherent structural cues that, when effectively leveraged, can significantly enhance the precision and reliability of knowledge extraction for populating knowledge graphs (KGs) [3,55]. However, their heterogeneity, complex layouts, and domain-specific semantics often demand tailored approaches rather than generic natural language processing (NLP) models alone.
Techniques for Structured and Semi-Structured Data Extraction
| Technique / Framework | Target Data Type | Core Mechanisms | KAB Addressed / Benefit | Limitations / Challenges |
|---|---|---|---|---|
| MatSKRAFT | Scientific tables (materials science) | GNNs for table representation, constraint-driven learning, domain-specific rules, data augmentation. | Large-scale knowledge extraction from complex layouts, handles heterogeneous reporting, identifies rare properties. | Domain-specific (not generalizable to all tables), complex rule engineering. |
| AxCELL | LaTeX source files (ML papers) | LaTeX structural information, ULMFiT classifiers, semantic segmentation, Bayesian inference for linking. | Automated extraction of (task, dataset, metric) tuples, populates leaderboards, precise. | Relies on LaTeX structure, not applicable to generic PDFs, requires context-rich text. |
| Entity & Type Recognition | KGs, databases, structured text | Schema/instance-level alignment, property-based similarity, Formal Concept Analysis. | Extends/refines KGs, resolves ambiguity, handles conceptual hierarchies. | Manual mapping effort, semantic heterogeneity challenges. |
| HKGB | Electronic Medical Records (EMR) | Human-in-the-loop validation, concept/relation mapping. | Semi-automatic KG construction, handles unstructured and structured parts. | Extensive human intervention, scalability issues. |
| LLM-driven Extraction | General semi-structured text | LLMs generate structured output (e.g., JSON) from instructions/examples. | Flexible, handles diverse formats, reduces manual rule specification. | Hallucination risk, lack of detailed algorithms for arbitrary external sources, not always more precise than specialized. |
| EneRex | Full-text scholarly articles | Weakly-supervised learning, syntactic patterns, NER. | Extracts technical facets (code, datasets, methods), identifies research trends. | Focuses on specific facets, manual refinement often needed for noise. |
A prominent framework specifically designed for handling highly structured data within scientific literature is Matskraft, which targets “large-scale materials knowledge extraction from scientific tables” [65]. Matskraft’s architectural choices are deeply rooted in addressing the unique complexities of this data format. It employs Graph Neural Networks (GNNs) to represent tables as graphs, enabling constraint-driven learning and domain-specific post-processing rules for disambiguation across heterogeneous reporting formats. For instance, GNN-1 is used for property extraction, achieving an 88.68% F1 score for 18 properties. Composition extraction utilizes specialized GNN-based architectures (GNN-2 for Single-Cell Composition tables and GNN-3 for Multiple-Cell Composition and Partial-Information tables) to navigate varying table structures and reporting conventions, yielding an overall 71.35% F1 score. Unit extraction, crucial for scientific data, is managed by a modular, rule-based framework combining dictionary-based matching, property-specific regular expressions, and physicochemical validation protocols, which achieves an impressive 97.18% overall accuracy. This multi-pronged approach underscores the necessity of combining structural analysis, machine learning, and domain knowledge to accurately interpret tabular data, which often contains implicit semantic relationships and abbreviations not readily understood by general text-based NLP models [65].
In contrast, while many systems focus on extracting structured information from unstructured text, or utilize existing structured KGs, fewer directly tackle the intricate parsing of complex semi-structured documents. For example, systems designed to extract knowledge from unstructured text to build KGs [2,11,74] typically do not detail methodologies for scientific tables. Similarly, frameworks that primarily leverage pre-existing structured knowledge bases for tasks like language model pre-training or knowledge injection, such as those that process Wikidata KG triples or integrate various domain-specific KGs, do not focus on extracting from raw semi-structured sources [1,7,16,40,71]. Even Large Language Models (LLMs), despite their ability to generate structured output or interpret information from generated text, often lack detailed algorithms for robust extraction from arbitrary external semi-structured sources like scientific tables [12,52,60,68]. When LLMs are applied to general information extraction, they may even fall short of specialized small models in precision for structured knowledge extraction, and converting inherently structured graphs into text can lead to semantic loss [12]. Other approaches, such as StructSense, leverage existing ML libraries like GROBID for initial PDF parsing but focus their novelty on agentic LLM orchestration and human-in-the-loop validation rather than developing new layout-based extraction algorithms [70]. EneRex, while processing scholarly documents, converts full text into structured representations and applies NER, but does not detail methodologies for handling scientific tables or “composition-property” data [51].
However, some systems combine structural and semantic understanding for automated results extraction in scholarly information. Axcell represents a sophisticated approach by utilizing structural information from LaTeX sources to extract entire tables, a key differentiator from methods reliant on noisy PDF parsing [41]. It employs a ULMFiT-based classifier for table type categorization (e.g., leaderboard, ablation) and semantic segmentation of cells (e.g., dataset, metric, model), integrating “handcrafted features” (like cell position and style) and contextual text fragments. For each numeric cell, Axcell generates multiple contexts (table, caption, mentions, abstract, paper) to aid in linking values to specific performance records using a Bayesian inference model [41]. This demonstrates how a combination of structural awareness, learned classifications, and contextual NLP contributes significantly to accuracy and efficiency in automated results extraction from scholarly tables.
Entity and type recognition algorithms play a crucial role in extending and refining knowledge graphs by identifying and classifying structured knowledge elements. The framework presented in [31] focuses on schema-level and instance-level entity type recognition within KGs, which involves aligning candidate entity types and instances with reference types. This is achieved by leveraging features derived from properties and various similarity metrics, implicitly addressing ambiguities arising from semantic heterogeneity during concept alignment [31]. Other methods also contribute to this area: AI-KG employs NLP tools and semantic clustering to extract predefined entity types and relations, utilizing an overlapping strategy [3]. For sensitive domains, HKGB processes Electronic Medical Records, involving human-in-the-loop validation for mapping definitions and concept extraction from both unstructured and structured parts [3]. The careful handling of diverse structured knowledge types within existing KGs, such as object entities, quantities, and dates, also requires sophisticated string matching, regular expressions, and structured parsing techniques for accurate alignment and recognition [1]. Entity linking, as seen in revisiting_the_knowledge_injection_frameworks, is a crucial step for aligning textual mentions with entries in structured KBs, effectively performing entity recognition and disambiguation in a broader context.
Despite significant advancements, several limitations and areas for improvement persist. A major challenge in extracting knowledge from structured and semi-structured sources is the “lack of tools supporting the (semi-)automatic definition of mappings” from these diverse sources to a target ontology or KG schema, often necessitating manual effort [3]. The heterogeneity of data formats, from web content to log data and scientific tables, each with unique structural characteristics, makes a one-size-fits-all solution difficult [55]. For web data, issues of uncertain facts and the need for reliable source selection and quality control are paramount [55]. Scalability is also a concern; for instance, the manual definition of relations in systems like KnowMap can limit their generalizability to unforeseen semi-structured inputs [44]. Future research should focus on developing more robust and autonomous tools for mapping definitions, enhancing LLMs’ inherent capabilities to process and interpret complex structured data without significant semantic loss, and integrating diverse structured and unstructured information streams for comprehensive knowledge acquisition. Furthermore, addressing the specific challenges of quantifying uncertainty in extracted facts from dynamic and potentially unreliable semi-structured sources remains an open question [55]. Continued efforts in domain-specific adaptations, like those seen in Matskraft for materials science, will be critical for high-fidelity knowledge extraction in specialized fields.
5.1.4 Model Behavior Extraction and Replication Algorithms
Model Behavior Extraction and Replication Algorithms
| Algorithm Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Black-Box Replication | Replicates input-output behavior of a target model. | Transfers functional knowledge from secret models, optimizes query costs. | Active Learning (Uncertainty, K-center, Adversarial, DFAL), CEGA (GNNs). | Lacks internal insight, effectiveness against defenses, limited to classification. |
| Internal Model Behavior Extraction (Interpretability) | Understands how models acquire, store, and process knowledge. | Enhances transparency, enables debugging, supports knowledge editing. | Often architecture-dependent, reliability of interpretability methods. | |
| Knowledge Localization & Editing | Pinpoints specific components for knowledge storage/processing. | Enables direct modification of knowledge, insights into model plasticity. | Knowledge Neurons, ROME, PMET (for LLMs). | Reliability of causal tracing, side effects on general capabilities. |
| Intervention & Circuit Discovery | Systematically perturbs internal components to find causal links. | Reveals computational subgraphs (circuits) governing knowledge. | EAP-IG (Knowledge Circuits), causal tracing, activation patching. | Computationally intensive, relies on architectural assumptions. |
| Probing & Implicit Parameter Extraction | Trains simpler models to extract representations from complex models. | Diagnoses linear knowledge encoding, extracts implicit priors. | P-Probing, Q-Probing (LLM hidden states), AutoElicit (LLM priors). | Often limited to linear encoding, not for general model replication. |
| Feature Attribution & Visualization | Identifies input data responsible for predictions. | Enhances human interpretability, visualizes learned patterns. | GradCam, DeepLift, Deep SHAP, learned filter visualizations. | Falls short of true explainability (“why”), can be computationally intensive. |
| Concept Discovery | Extracts abstract concepts from latent spaces. | Makes black-box AI strategies interpretable, bridges human-AI gap. | AlphaZero (convex optimization for sparse vectors). | Linearity assumption, methodological limitations for transfer. |
| Uncertainty & Confidence Extraction | Quantifies model’s confidence in predictions. | Guides data acquisition (AL), improves data quality (re-annotation). | Confidence scores (NER), entropy. | May not reflect true model uncertainty. |
| Knowledge Distillation | Transfers functional knowledge from teacher to student models. | Replicates behavior efficiently, enables smaller models. | DWML (mutual learning), traditional KD (KL divergence). | Can lose nuances, increased complexity not always better. |
Model behavior extraction and replication algorithms represent a critical area in understanding, analyzing, and transferring the capabilities of artificial intelligence systems. Unlike traditional information extraction (IE), which primarily focuses on identifying and structuring factual entities and relations from external unstructured data [48], model behavior extraction targets the implicit logic, decision boundaries, internal representations, or specific functional mechanisms inherent within a trained model. This distinction underscores a fundamental shift from extracting explicit knowledge from data to understanding and replicating the model’s acquired knowledge and its utilization. A significant challenge in this domain, particularly in black-box interaction scenarios, is the optimization of queries to efficiently elicit comprehensive behavioral information from the target model [15].
Model behavior extraction and replication methods can be broadly categorized into those aiming for black-box functional replication, those focusing on internal interpretability, and knowledge distillation techniques.
Black-Box Model Replication and Query Optimization
In adversarial contexts, the objective is to replicate the input-output mapping of a secret target model ($f$) by training a substitute model ($\tilde{f}$) solely through external observations. The primary challenge here lies in efficiently querying the black-box model to gather sufficient and informative training data for the substitute.
Several active learning strategies have been developed to optimize this querying process, maximizing information gain while minimizing query costs. For Deep Neural Networks (DNNs), a prominent framework [15] employs diverse query selection algorithms:
- The Uncertainty strategy selects samples where the target model exhibits high entropy in its predicted probability vectors, indicating instances of ambiguity or difficulty.
- The K-center strategy aims for data diversity by greedily choosing samples whose predicted probability vectors are maximally distant from already selected cluster centers.
- The Adversarial strategy, specifically DeepFool Active Learning (DFAL), identifies samples close to the decision boundary by finding the minimum perturbation required for misclassification. This approach leverages the adversary’s ability to compute gradients on their own interim substitute model to probe the secret model’s boundaries.
- An Adversarial+K-center ensemble strategy combines DFAL’s boundary-seeking efficacy with K-center’s diversity, demonstrating superior performance in various image classification tasks, winning in 13 out of 20 experiments [15].
For Graph Neural Networks (GNNs), CEGA (Cost-Effective Approach for Graph-based Model Extraction and Acquisition) utilizes an adaptive node selection method [45]. CEGA’s approach integrates three criteria through a weighted average ranking ($\mathcal{R}^\gamma = \omega_1(\gamma) \mathcal{R}_1^\gamma + \omega_2(\gamma) \mathcal{R}_2^\gamma + \omega_3(\gamma) \mathcal{R}_3^\gamma$), with dynamically adjusted weights over learning cycles:
- Representativeness: Employs PageRank to prioritize structurally important nodes.
- Uncertainty: Selects nodes with high entropy in softmax predictions or sensitivity to Gaussian perturbations, akin to being near decision boundaries.
- Diversity: Uses K-Means clustering on node embeddings to ensure broad exploration of the graph space.
Both CEGA and the framework for DNNs share the underlying theoretical foundation of active learning, seeking to strategically sample the input space to efficiently approximate the target model’s behavior. However, CEGA’s adaptive weighting and graph-specific criteria represent a domain-specific adaptation, while the DNN framework leverages adversarial perturbations to probe decision boundaries more directly. A key limitation of these black-box replication methods is their focus on input-output behavior, precluding insights into the secret model’s internal mechanisms or reasoning [15]. Furthermore, their effectiveness against target models designed to return noisy or uncertain predictions as a defense mechanism remains an unaddressed challenge [15].
Internal Model Behavior Extraction: Interpretability and Knowledge Understanding
Beyond mere input-output replication, a significant line of research focuses on extracting internal model behavior to understand how models acquire, store, and process knowledge, often for interpretability or knowledge editing purposes.
-
Knowledge Localization and Editing: These methods aim to pinpoint specific architectural components responsible for storing or processing particular knowledge. In Large Language Models (LLMs), techniques like Knowledge Neurons use gradient-based attribution to identify Feed-Forward Network (FFN) components as knowledge storage locations, enabling direct modification of value slots [20]. ROME employs causal tracing to suggest that Transformer MLPs act as linear associative memories, allowing direct rank-one updates to MLP weights to alter behavior [20]. Similarly, PMET focuses on precisely updating FFN weights by optimizing Transformer hidden states to memorize target knowledge [20]. While these methods assume knowledge is localizable to specific, modifiable components, the reliability of causal tracing for knowledge localization has been critiqued as potentially unreliable, highlighting an
interpretabilitydeficiency[20]. -
Intervention-based Methods and Circuit Discovery: These approaches involve systematically perturbing internal model components to identify their causal influence on outputs. Intervention-based methods typically involve “Clean run,” “Corrupted run,” and “Restoration run” experiments, using techniques like causal tracing, activation patching, and causal scrubbing to pinpoint components causally linked to specific knowledge utilization [30]. For LLMs, Edge Attribution Patching with Integrated Gradients (EAP-IG) identifies “knowledge circuits” by assigning importance scores to computational subgraphs (edges) based on their causal effect on the loss. The importance score $S(e)$ for an edge $e=(u,v)$ is defined as: \(S(e)=\left(z_u^{\prime}-z_u\right) \frac{1}{m} \sum_{k=1}^m \frac{\partial L\left(z^{\prime}+\frac{k}{m}\left(z-z^{\prime}\right)\right)}{\partial z_v}\) where $z_u$ and $z’_u$ are clean and corrupted activations, and $L$ is the loss, effectively quantifying the contribution of specific computational paths to factual recall [34]. These methods are highly dependent on the model’s architectural choices, focusing on the flow of information through specific layers or connections.
-
Probing and Implicit Parameter Extraction: This category involves training simpler, interpretable models to “probe” or extract representations from a more complex model. P-Probing and Q-Probing train linear classifiers on LLM hidden states to predict biographical attributes, assessing if and where knowledge is linearly stored in relation to specific input tokens or names [73]. AutoElicit extracts LLMs’ implicit priors and in-context posterior distributions by fitting linear models (via Maximum Likelihood Estimation) to the LLM’s predictions, providing “new visibility into the LLM’s predictive process” [19]. While these are powerful diagnostic tools, they are not designed for general model replication in an adversarial sense, but rather for understanding internal knowledge representation.
-
Feature Attribution and Visualization: For deep learning models, particularly in computer vision, techniques like Attribution Maps (perturbation-based or backpropagation-based, e.g., GradCam, DeepLift, Deep SHAP) identify which input data (e.g., pixels) are responsible for a model’s prediction [39]. Visualization of learned filters in CNNs further illustrates the patterns models are sensitive to. These methods aim to enhance human interpretability but often fall short of true “explainability” (answering why a model behaves in a certain causal manner) and can be computationally intensive [39].
-
Concept Discovery: In advanced AI systems like AlphaZero, extracting “concepts” that lead to strategic plans is achieved by identifying sparse vectors in the model’s latent space through convex optimization. This process minimizes an $L_1$ norm subject to constraints derived from behavioral differences between optimal and suboptimal MCTS rollouts [54]. The teachability framework then validates this by replicating concept-driven behavior in a “student network.” A
methodological limitationhere is the assumption of linear concept encoding, and thearchitectural mismatchcan limit direct transfer to other model types. This work also critically assessessaliency-based interpretability methodsas potentially “unfalsifiable” and prone to “provably wrong results” [54]. -
Uncertainty and Confidence Extraction: Model behavior extraction can also involve quantifying a model’s uncertainty. For instance, confidence scores from Named Entity Recognition (NER) classifiers (e.g., sequence probabilities for BiLSTM-CRF or average logits for BioBERT) are extracted to estimate
model uncertainty. This information is then used to prioritize sentences for human re-annotation, thereby guiding knowledge acquisition and improving data quality [25].
Knowledge Distillation for Behavior Replication
Knowledge Distillation (KD) techniques aim to transfer functional knowledge from a larger, more complex “teacher” model to a smaller “student” model, effectively replicating its behavior for efficiency or deployment on resource-constrained devices. Traditional KD minimizes the Kullback-Leibler (KL) divergence between the student and teacher’s output logits [8]. Diversity Induced Weighted Mutual Learning (DWML) extends this by allowing multiple “peer” student models to collaboratively learn from each other’s behavior, aligning their class posteriors through weighted KL divergence terms. However, experiments suggest that simpler self-distillation methods can sometimes outperform complex mutual learning approaches on syntactic tasks, indicating that increased complexity does not always translate to superior behavior replication in practice [8].
General Model Behavior Analysis and Evaluation
Beyond direct replication or fine-grained internal extraction, several studies focus on observing and characterizing general aspects of model behavior:
- Memorization studies quantify verbatim and factual memorization in LLMs to understand their knowledge acquisition and recall mechanisms [60].
- The KAU gap framework extracts correctly predicted encyclopedic facts from frozen Pre-trained Language Models (PLMs) to define acquired knowledge, subsequently measuring its utilization on downstream tasks [53].
- Analysis of knowledge injection frameworks reveals how models process injected knowledge by comparing hidden states and outputs, sometimes exposing
Ineffective Knowledge Utilizationwhere models do not functionally differentiate between aligned and random knowledge inputs [7]. - Evaluation of domain generalizability assesses off-the-shelf NLP models’ zero-shot behavior in new domains, identifying specific failure modes like struggles with uncommon syntax or acronyms, characterizing their
behavioral flawsin specialized contexts [48]. - Latent entity behavior prediction trains meta-models to predict the behavior (answers) of a latent entity and adaptively selects questions to reduce uncertainty [13].
- Environmental dynamics extraction methods like Latplan learn state representations, action models, and preconditions from visual observations to replicate an environment’s behavior in a symbolic, interpretable PDDL model for classical planning [28].
- A teacher agent can algorithmically extract and analyze a student agent’s reasoning steps to identify errors and abstract generalizable problem-solving strategies from execution trajectories [33].
Limitations, Gaps, and Future Research
The landscape of model behavior extraction and replication presents a dichotomy between black-box and white-box approaches. While black-box methods, particularly those leveraging advanced query optimization, excel at functional input-output replication, they intrinsically lack insight into the model’s internal reasoning. Conversely, white-box methods offer greater interpretability by dissecting internal mechanisms, but they are often highly architecture-dependent, making them less generalizable.
A critical area for improvement lies in the reliability of interpretability methods. Concerns about the dependability of causal tracing for knowledge localization [20] and the recognized shortcomings of saliency-based methods (e.g., “unfalsifiability,” “cognitive bias,” and “provably wrong results”) [54] underscore the need for more robust and verifiable techniques that genuinely explain causal links.
Query optimization in black-box scenarios also faces limitations, especially when confronted with sophisticated defensive mechanisms. Strategies that can effectively navigate models designed to return uncertain or noisy predictions as a deterrent remain an important research direction [15]. The generalizability of extracted concepts and mechanisms is another significant challenge. Many internal extraction techniques are tailored to specific model architectures (e.g., Transformer FFNs, AlphaZero’s latent space), restricting their applicability across diverse model types, and assumptions like linear concept encoding can be a methodological limitation [54].
Future research should focus on developing methods that bridge the gap between black-box efficiency and white-box interpretability. This includes creating adaptive query strategies resilient to defensive measures, advancing architecture-agnostic techniques for internal behavior extraction, and developing unified metrics to assess the completeness and fidelity of extracted behaviors. Furthermore, addressing observed Ineffective Knowledge Utilization [7] by developing methods to not only extract but also enforce more robust knowledge processing mechanisms is crucial for advancing reliable and explainable AI.
5.2 Knowledge Acquisition and Refinement Algorithms for Pre-trained Language Models (PLMs) and Large Language Models (LLMs)
The rapid evolution of Pre-trained Language Models (PLMs) and Large Language Models (LLMs) has underscored the critical need for sophisticated algorithms to facilitate knowledge acquisition and refinement, thereby mitigating the inherent bottlenecks in updating and expanding their vast knowledge bases. This section provides a comprehensive overview of cutting-edge algorithmic approaches spanning prompt engineering, synthetic knowledge ingestion, and autonomous self-tuning mechanisms, all aimed at transforming LLMs into more dynamic and adaptive knowledge systems. These methodologies are crucial for enhancing model performance, ensuring factual consistency, and enabling continuous learning in diverse applications.
Prompt Engineering for Knowledge Elicitation
A foundational approach to knowledge acquisition from LLMs involves strategic prompt engineering, which leverages the model’s pre-trained parameters to elicit specific information or behaviors. Initially a manual and often laborious process [12,52], prompt engineering has advanced significantly with automated techniques, such as AutoPrompt, which optimizes prompt generation through gradient-guided search to maximize performance on downstream tasks [43]. This evolution enables LLMs to function as active knowledge acquisition agents, guiding them to extract nuanced information, construct knowledge graphs (e.g., SAC-KG [66]), or generate structured synthetic data (e.g., Ski for question-answer pairs [5]). Techniques like AutoElicit further extend this by enabling the elicitation of quantifiable expert priors, transforming LLMs into probabilistic knowledge sources for data-scarce domains [19]. A key distinction lies in the trade-offs between in-context learning (ICL), which implicitly guides LLMs through examples, and explicit prior elicitation, which directly extracts structured knowledge. While ICL offers flexibility, its efficacy is sensitive to example quality and phrasing, often leading to “knowledge conflicts” where LLMs prioritize internal, potentially outdated knowledge [20]. Prompt engineering faces challenges such as the hallucination propensity of LLMs, the lack of provenance for extracted knowledge, and the brittleness of automated prompt generation methods [43,55].
Synthetic Knowledge Ingestion and Knowledge Alignment
Beyond elicitation, proactively generating and integrating new knowledge—termed Synthetic Knowledge Ingestion (SKI)—is vital for enhancing LLM capabilities. This paradigm transforms raw or implicitly available knowledge into formats readily assimilable by LLMs. Methods include KG verbalization, where structured knowledge from sources like Wikidata is converted into natural language text to create corpora like KeLM [1]. LLMs are also employed to directly construct synthetic knowledge, such as generating graph reasoning data in GRAIL [63] or conceptual labels in CB-LLM [32]. Crucially, knowledge alignment and integration ensure consistency and coherence across diverse information sources. This involves implicit methods that modify LLM parameters directly through knowledge-injecting pre-training [12], knowledge editing [20], or continual learning strategies. Explicit alignment, conversely, leverages external context (e.g., Retrieval-Augmented Generation (RAG) [12,20]) or enforces structured outputs to ground LLM generations, as seen in StructSense for information extraction [70]. Challenges in SKI and alignment include semantic heterogeneity, schema reconciliation across multiple knowledge graphs [1,5], the risk of catastrophic forgetting in implicit methods, and knowledge conflicts arising from noisy external content [20].
Self-Tuning and Autonomous Knowledge Extraction
The ultimate goal in knowledge acquisition is to enable models to autonomously learn, adapt, and refine their knowledge bases without continuous human intervention. The self-tuning paradigm empowers LLMs to “self-teach” by generating their own learning tasks and spontaneously acquiring knowledge from new documents, as demonstrated by the Self-Tuning framework [68]. Systems like R1-Searcher++ employ reinforcement learning to enable LLMs to autonomously decide whether to use internal or external knowledge and to progressively enrich their internal representations through “External Knowledge Memorization” [27]. A significant advancement is LLM-driven autonomous ontology evolution, exemplified by Evo-DKD, which uses a dual knowledge decoding strategy within a closed reasoning loop to maintain, update, and evolve knowledge bases, effectively training itself over time [17]. This builds on earlier concepts like NELL, which continuously extracted information to populate its knowledge base [9]. Furthermore, autonomous knowledge refinement focuses on optimizing and disentangling existing representations to improve utility and robustness. Pluvio, for instance, uses a reinforcement learning agent for token pruning and a Conditional Variational Information Bottleneck (CVIB) to learn domain-invariant representations, effectively “forgetting” irrelevant details to enhance generalization [24]. Other techniques contributing to autonomous refinement include recursive bootstrapping [46] and reinforcement learning for optimizing knowledge capture, such as GRPO in LBMs [50].
Overarching Challenges and Future Directions
Despite these substantial advancements, several critical challenges remain. The pervasive issue of LLM hallucination continues to undermine the reliability and accuracy of autonomously acquired knowledge, often without sufficient provenance [12,55]. Computational costs and context length limitations hinder the scalability of many advanced self-tuning methods [50], while a persistent data dependency often limits truly unsupervised knowledge discovery [43]. The “Knowledge Acquisition/Utilization Gap,” where LLMs struggle to adequately disentangle complex external knowledge, further highlights a theoretical and practical deficit [7]. Future research must focus on developing robust self-correction mechanisms within LLMs, moving beyond external verifiers, and advancing adaptive elicitation frameworks that dynamically respond to real-time performance and knowledge gaps. Addressing the nuanced challenges of uncertainty in knowledge representation [55], achieving unified fusion models for diverse data types and granularities, and exploring the interaction between knowledge alignment and knowledge entropy [69] are crucial. Ultimately, fostering truly unsupervised, multimodal discovery and lifelong learning capabilities—where models can autonomously prioritize, integrate, and consolidate knowledge—will be essential for developing more intelligent, adaptive, and trustworthy LLM systems in an ever-evolving information landscape.
5.2.1 Prompt Engineering and Automated Knowledge Elicitation
Prompt engineering has emerged as a pivotal technique for eliciting and acquiring knowledge from Large Language Models (LLMs), fundamentally transforming them into more active knowledge acquisition agents by strategically querying their vast pre-trained knowledge bases [20,30,52].
Prompt Engineering and Automated Elicitation for LLM KAB
| Technique / Approach | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Manual Prompt Engineering | Human-designed textual inputs to guide LLM responses. | Basic knowledge elicitation, task specification. | - | Time-consuming, laborious, sensitive to phrasing, non-scalable. |
| Automated Prompt Generation | Algorithms optimize prompts to maximize task performance. | Automates prompt design, improves efficiency & effectiveness of elicitation. | AutoPrompt (gradient-guided search for “trigger tokens”). | Prompts can be uninterpretable, method can be brittle, requires labeled data for optimization. |
| In-Context Learning (ICL) | Providing relevant examples within the prompt. | Implicitly guides LLMs, avoids fine-tuning, flexible. | SAC-KG (example segments), MATSKRAFT (few-shot), KnowPrompt. | Dependent on example quality, sensitive to length/phrasing, knowledge conflicts. |
| Explicit Prior Elicitation | Directly extracts quantifiable knowledge (e.g., distributions). | Transforms LLMs into probabilistic knowledge sources, useful for data-scarce domains. | AutoElicit (generates Gaussian priors). | Requires careful algorithm design, LLM reliability, aggregation challenges. |
| Structured Output Prompts | Designs prompts to elicit machine-readable output formats. | Enables direct integration into structured systems (KGs), improves control. | KGValidator (Pydantic classes), DeepKE (custom schema), TeKGen. | Can lead to semantic loss, may struggle with complex structures. |
| Reasoning Prompts | Uses techniques like CoT, ToT, GoT to guide LLM reasoning. | Improves complex reasoning, reduces hallucination. | CoT, ToT, GoT (for LLMs). | Computationally intensive, effectiveness sensitive to prompt structure. |
| Probing LLM Knowledge | Generates specific queries to elicit factual information. | Diagnoses inherent knowledge, assesses extractability. | Soft-prompting, QA tasks (LAMA), LBMs (natural language summaries). | Often assumes linear encoding, may not reflect true understanding. |
This section analyzes the methodologies behind automated prompt generation, compares different LLM-driven elicitation techniques, and discusses the trade-offs between in-context learning and explicit prior elicitation.
The shift from manual prompt engineering, which is often described as time-consuming and laborious [12,18,20,30,44,48,52,59,60,66], to automated prompt generation is a significant advancement in this domain. One prominent example is AutoPrompt [43]. This algorithm automatically generates prompts to elicit knowledge from pre-trained language models (PLMs/LLMs) by optimizing the context provided to maximize performance on downstream tasks without fine-tuning. AutoPrompt’s methodology involves defining a prompt template with “trigger tokens” and then using a gradient-guided search to iteratively update these tokens. The optimization aims to maximize the label likelihood by computing a first-order approximation of the change in log-likelihood for swapping trigger tokens with others in the vocabulary. The candidate set $\mathcal{V}{\textrm{cand}}$ is selected as the top-$k$ tokens estimated to cause the greatest increase, calculated as:
\(\mathcal{V}_{\textrm{cand}} = \underset{w\in \mathcal{V}}{\text{top-}k} \left< \frac{\partial \log P(\text{true label})}{\partial \mathbf{w}_{\textrm{in}}^{(x_{\textrm{trig}}^{(j)})}}, \mathbf{w}_{\textrm{in}}^{(w)} \right>\)
where $\mathbf{w}{\textrm{in}}^{(x_{\textrm{trig}}^{(j)})}$ is the input embedding of the trigger token and $\mathbf{w}_{\textrm{in}}^{(w)}$ is the input embedding of candidate token $w$ [43]. This systematic optimization offers significant advantages over manual prompt engineering, as demonstrated by AutoPrompt’s performance gains (e.g., 43.34% P@1 for fact retrieval with AutoPrompt versus 31.10% for manual prompts on LAMA) [43]. However, a notable limitation is that the generated prompts can be ungrammatical and lack interpretability, posing a Interpretability challenge [43]. The greedy nature of the gradient-guided search can also lead to brittleness and optimization issues, and the method requires labeled training data, introducing a data dependency [43].
Beyond AutoPrompt, several other techniques transform LLMs into active knowledge acquisition agents by strategically querying them. For instance, in the construction of Knowledge Graphs (KGs), SAC-KG employs an “instruction segment” and leverages an Open KG Retriever to automatically fetch relevant in-context examples from DBpedia, mitigating knowledge hallucination and improving output controllability [66]. It further refines LLM output through reprompting for error correction [66]. Similarly, Ski uses specific meta-prompts ($P_{fs}$ for fine-grained synthesis and $P_{ig}$ for interleaved generation) to guide LLMs in generating synthetic knowledge like structured question-answer pairs [5]. The Self-Teaching strategy also relies on predefined prompt templates to guide LLMs in generating their own learning materials from raw documents, effectively acting as an automated knowledge elicitation mechanism [68]. Agent KB employs a prompt template to guide an LLM in generating structured “experiences” from failure cases and uses adaptive elicitation to infer and apply domain-specific transformations, reusing successful transformations as few-shot exemplars [33]. GRAIL utilizes GPT-4o with predefined instructions for multi-turn interactions to generate graph reasoning data, automating knowledge elicitation for data synthesis [63]. Bench4KE further evaluates systems using various prompting techniques, including conversational prompting (e.g., OntoChat) and structured prompt templates (e.g., NeOn-GPT) [14].
Comparing different LLM-driven elicitation techniques reveals their varied effectiveness in capturing nuanced expert knowledge and their robustness against biases. AutoElicit [19] specifically focuses on algorithms for expert prior elicitation, which involves designing an initial human-written prompt and then automatically generating diverse variations of this prompt using an LLM. For each varied prompt, the LLM is queried to output specific quantifiable knowledge, such as the mean and standard deviation of a Gaussian prior $(\mu_k, \sigma_k)$ for features in a linear model. These individual priors are then combined into a mixture of Gaussians: $\Pr_{M, T}(\theta) = \sum_{k=1}^K \pi_k \mathcal{N} ( \theta |
\mu_k, {\sigma_k}^2 )$ [19]. This systematic process leverages the LLM’s pre-trained knowledge to generate informative priors, improving predictive performance in data-scarce scenarios, and is evaluated by posterior accuracy and mean squared error [19]. A key aspect of AutoElicit is its automated prompt variation, which aims to reduce sensitivity to specific phrasing and capture a broader range of the LLM’s embedded knowledge [19]. |
Many techniques emphasize structured output and prompt-based guidance for specific tasks. For knowledge graph completion, Better Together structures input as a “verbalized query” combined with verbalized neighborhood information to guide the LLM in generating target entities, demonstrating that the manner of knowledge presentation impacts performance [49]. KGValidator uses a generic model prompt with Instructor library and Pydantic classes to ensure structured outputs for KG triple validation, eliciting specific knowledge in a machine-readable format [40]. DeepKE employs KnowPrompt for few-shot Relation Extraction, incorporating external knowledge into prompt design and using prompt-guided attention for Named Entity Recognition, thereby steering the model’s focus with sparse data [38]. The TeKGen model uses a fixed structured input format for KG triples to generate natural language sentences, a basic form of prompt engineering for data-to-text tasks [1]. Similarly, Evo-DKD uses prompt-based mode control to guide LLMs in generating either structured ontology edits or natural language explanations [17]. In Retrieval-Augmented Generation (RAG), “Graph Prompting” transforms graph-structured knowledge into LLM-digestible formats, including “Topology-Aware Prompting” that explicitly encodes nodes, edges, and relationships, and “Text Prompting” which converts graph knowledge into linear narratives [71]. Systems like MindMap and KGP generate reasoning paths and retrieve contexts to inform LLM prompts, while MedGraphRAG refines answers iteratively through prompts [71]. DKA designs prompts to make LLMs explicitly decompose complex questions into sub-questions for image-based and knowledge-based acquisition, leading to precise and disentangled knowledge requirements [61]. For monitoring external knowledge, R1-Searcher++ trains LLMs to generate structured search queries and internal reasoning, enforcing format correctness with a reward mechanism [27]. StructSense uses “task configurations” for prompt engineering to elicit structured information [70].
Probing LLMs’ internal knowledge also relies on prompt engineering. Soft-prompting is used to generate specific queries that elicit factual information (tail entities) stored within the model’s parameters in a zero-shot setting [53]. Factual recall tasks convert subject-relation pairs into query strings (e.g., “s lives in the city of ___”) to probe LLM knowledge [34,69]. The LBMs framework uses prompts to guide an encoder LLM in generating textual summaries of student knowledge states, further optimizing this process with Group Relative Policy Optimization (GRPO) to encourage accurate and structurally compliant summaries [50].
A critical challenge is the inherent hallucination propensity of LLMs, which directly impacts the reliability and accuracy of elicited knowledge [52]. Furthermore, LLMs often do not provide provenance or reliability information for extracted knowledge, creating interpretability and data dependency issues, especially for numerical facts and long-tail entities [55]. This necessitates mechanisms to validate LLM-elicited knowledge without extensive manual review and designing prompts to explicitly solicit confidence scores or provenance [55].
The trade-offs between in-context learning (ICL) and explicit prior elicitation are central to LLM-driven knowledge acquisition. ICL, as employed by SAC-KG through example segments and by MATSKRAFT with strategic few-shot learning, leverages relevant examples within the prompt to encourage the LLM to generate content in the correct format and style [65,66]. KnowPrompt and the injection of conceptual knowledge ($k_c$) within prompts also fall into this category, demonstrating improved accuracy by providing refined knowledge contextualized within the query [7,38]. Concept Bottleneck LLMs leverage human-designed in-context examples to automatically generate domain-specific concepts, demonstrating an efficient and automated method of knowledge acquisition for interpretable systems [32]. The primary advantage of ICL is its ability to implicitly guide LLMs’ generative capabilities without requiring explicit model fine-tuning or extensive data annotation. However, its quality is highly dependent on the relevance and diversity of provided examples, and its performance can be sensitive to prompt length, phrasing, and underlying biases in the model’s pre-training [66]. In contrast, explicit prior elicitation, exemplified by AutoElicit, aims to directly extract quantifiable knowledge (e.g., statistical distributions) that can be formally incorporated into downstream models. This approach transforms LLMs into probabilistic knowledge sources, particularly beneficial for data-scarce domains. While explicit elicitation offers more structured and potentially more robust knowledge for specific applications, it requires careful algorithm design for prompt generation and knowledge aggregation, and still faces the challenge of LLM reliability [19]. The efficacy of elicited knowledge can also be hampered by LLMs favoring their internal, possibly outdated, knowledge over provided context, leading to “knowledge conflicts” [20].
Despite significant progress, limitations and areas for improvement persist. A recurring challenge is the laborious nature of high-quality prompt engineering, even in partially automated systems, indicating a manual effort bottleneck and scalability challenges for acquiring higher expressiveness in prompts [12,44,60]. The lack of provenance and reliability information for elicited knowledge remains a critical issue [55]. Future research should focus on developing adaptive elicitation frameworks that dynamically modify prompts or examples based on the LLM’s real-time performance or knowledge gaps, rather than relying on fixed templates [66]. Further investigation is needed into how to overcome the brittleness of gradient-guided prompt searches [43] and how knowledge entropy decay might affect the efficacy of different prompt engineering strategies [69]. Addressing these limitations will require novel algorithms for automated and adaptive prompt optimization, improved mechanisms for soliciting confidence and provenance from LLMs, and deeper understanding of how to integrate external structured knowledge sources (like KGs) more seamlessly and dynamically within prompting strategies.
5.2.2 Synthetic Knowledge Ingestion and Knowledge Alignment
Synthetic Knowledge Ingestion (SKI) represents a proactive paradigm for enhancing Large Language Models (LLMs) by generating and integrating new knowledge into their learning processes or operational frameworks.
Synthetic Knowledge Ingestion & Alignment for LLM KAB
| Strategy Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Synthetic Knowledge Ingestion (SKI) | Generates new knowledge in LLM-digestible formats. | Enhances LLM capabilities, addresses knowledge deficits, reduces annotation. | Relies on generative LLM quality/bias, semantic heterogeneity, noise. | |
| KG Verbalization | Converts structured KG data into natural language text. | Ingests structured knowledge, bridges architectural mismatch. | TeKGen (Wikidata to KeLM Corpus). | Semantic loss, hallucination risk, limited to textual-level alignment. |
| Fine-Grained Synthesis | Generates specific types of structured knowledge (e.g., Q&A). | Creates high-quality training data, optimizes for specific tasks. | Ski (Q&A from n-gram contexts), GRAIL (graph reasoning data). | Quality of generated data, requires careful meta-prompt design. |
| LLM Construction | LLMs directly generate structured knowledge from instructions. | Automates KG construction/refinement, extracts implicit knowledge. | SAC-KG (domain KGs), CB-LLM (concept labels), AutoElicit (probabilistic priors). | Hallucination risk, reliability of LLM-generated facts, requires validation. |
| Knowledge Alignment | Integrates and ensures consistency across knowledge sources. | Mitigates outdated/conflicting info, improves factual accuracy. | Semantic heterogeneity, schema reconciliation, catastrophic forgetting. | |
| Implicit Parametric Alignment | Modifies LLM internal parameters during training/fine-tuning. | Infuses structured understanding, preserves existing knowledge. | KG-injecting pre-training (input/intermediate/objective layers), Knowledge Editing, Continual Learning. | Semantic loss/interference, side effects, catastrophic forgetting, “ineffective utilization.” |
| Explicit Contextual Alignment | Provides external info as context, enforces consistency. | Grounds LLM responses, ensures factual accuracy, real-time updates. | Retrieval-Augmented Generation (RAG), IRCoT, ReAct (web-enhanced). | Scalability of external memory, noisy sources, inference overhead, knowledge conflicts. |
| KG-Centric Alignment | Reconciles knowledge from diverse structured sources. | Reduces redundancy, resolves inconsistencies, handles granularity. | Entity Alignment, Knowledge Fusion, KnowMap (embedding alignment), KGValidator. | Assumes deterministic knowledge, struggles with granularity/mixed types, computational cost. |
At its core, SKI aims to transform raw, unstructured, or implicitly available knowledge into formats that are “readily assimilable and digestible” by LLMs, often through fine-grained synthesis, interleaved generation, and assemble augmentation strategies [5]. This process fundamentally contributes to knowledge refinement and injection, addressing the limitations of static pre-trained models.
Mechanisms and Variations of Synthetic Knowledge Ingestion
Several frameworks exemplify the generation and integration of synthetic knowledge for LLM enhancement. One prominent approach is KG verbalization, as demonstrated by the TeKGen system which converts the entire English Wikidata Knowledge Graph (KG) into natural language text, forming the KeLM Corpus [1]. This process verbally ingests structured knowledge by aligning KG triples with Wikipedia text using distant supervision, followed by sequential fine-tuning of a T5 model to reduce hallucination and improve fluency. Semantic quality filtering further refines this verbalized knowledge using a BERT-based classifier to discard low-quality sentences, ensuring better alignment with the input KG triples [1]. The resulting KeLM Corpus is then integrated with retrieval LMs like REALM to inject knowledge during pre-training and inference. However, a limitation of this approach is its primary focus on textual-level alignment and its reliance on a single KG, precluding explicit entity mapping or schema reconciliation across distinct KGs [1].
Another advanced SKI method involves fine-grained synthesis and augmentation. For instance, the Ski framework generates hypothetical questions or question-context pairs (Ski-Q-n, Ski-QC-n) based on n-gram knowledge contexts derived from raw documents, leveraging an LLM with specific meta-prompts [5]. This is extended by interleaved generation, simultaneously producing questions and concise answers (Ski-QA-n) or question-context-answer triples (Ski-QCA-n). These synthetically generated datasets are then augmented and integrated to enhance Retrieval Augmented Generation (RAG), Supervised Fine-tuning (SFT), or Continual Pre-training (CPT) of LLMs. This approach is effective in transforming unstructured knowledge into a question-augmented representation highly suitable for LLM assimilation [5].
LLMs themselves are increasingly employed to construct synthetic knowledge. In the GRAIL framework, a closed-source LLM (GPT-4o) interacts with knowledge graphs to synthesize graph reasoning data, generating exploration trajectories and correct responses. This raw synthetic data undergoes Shortest Path Refinement which removes redundant exploration steps, ensuring the retained trajectories adhere to a “minimality principle” essential for effective reinforcement learning by eliminating high-path redundancy and noise [63]. Similarly, LLMs can be fine-tuned to extract structured information from text and populate KGs, a form of synthetic knowledge ingestion where LLMs generate structured knowledge to extend existing KGs [48]. The SAC-KG framework further refines this by using existing KGs to guide LLMs in generating new KG triples, followed by Verifier and Pruner components for knowledge refinement, correcting format errors and filtering low-quality entities [66].
Beyond structured knowledge generation, SKI encompasses methods that synthesize knowledge from LLMs’ implicit capabilities. AutoElicit extracts probabilistic priors from LLMs’ general knowledge, structuring their output into Gaussian parameters to create usable, structured formats for downstream predictive models [19]. For specialized concept learning, CB-LLM generates “pseudo concept labels” for text samples by calculating cosine similarity between text and concept embeddings, which are then refined through “Automatic Concept Correction” to align with human reasoning [32].
The critical role of advanced knowledge representations in facilitating SKI is evident across these approaches. Whether it is the verbalization of KGs into natural language text [1], the formulation of knowledge into question-augmented representations [5], the structuring of LLM outputs into probabilistic priors [19], or the use of property-based similarity metrics and Formal Concept Analysis (FCA) lattices for KG extension [31]. The conceptual knowledge approach in [7], which “purifies and prunes” complex wiki triples into concise (title, type, concept) triplets, demonstrates that a cleaner, more abstract representation can overcome Knowledge Complexity Mismatch and improve LLM utilization.
Knowledge Alignment and Integration Techniques
Knowledge alignment and integration are crucial for enhancing LLMs, particularly in handling semantic heterogeneity and maintaining knowledge consistency. These techniques can be broadly categorized into implicit parameter modifications, explicit contextual alignment, and general knowledge graph-centric alignment.
Implicit Knowledge Ingestion and Alignment: These methods integrate knowledge by modifying the LLM’s internal parameters or representations.
- Knowledge-injecting Pre-training covers strategies like
Input-layer Injection(converting KGs to natural language for data augmentation),Intermediate-layer Injection(integrating KG embeddings via attention mechanisms to align textual semantics with structured knowledge), andObjective-layer Injection(adding a KG embedding loss in multi-task learning to guide the LLM to learn both textual and structural information simultaneously) [12]. WhileInput-layer Injectioncan lead tosemantic lossdue to text conversion,Intermediate-layer Injectionfaces potentialinterference between textual semantic signals and knowledge structure signals[12]. - Knowledge Editing algorithms directly modify LLM parameters to inject new factual knowledge, through
weight shifts(e.g., MEND using low-rank components) ordirect modification(e.g., MEMIT scaling to thousands of facts simultaneously) [20]. - Continual Learning continuously updates parameters to acquire new knowledge while mitigating forgetting, using techniques like regularization, architectural adjustments (e.g., K-Adapter), or replay methods [20].
- Implicit Knowledge Injection like GLM (Graph-guided Masked Language Model) uses existing KGs to guide masking and negative sampling during pre-training, influencing the LM’s internal representations to capture structured information from raw text [42]. This implicit approach, however, offers less direct control over which specific knowledge is encoded or how it is aligned compared to explicit methods.
- Knowledge-enhanced word embeddings involve jointly embedding words and KG entities, optimizing both representations to handle alignment challenges, even with imperfect initial text-KG alignment [72].
Explicit Knowledge Alignment: These approaches align LLM outputs with external, often up-to-date, knowledge by providing it as context or enforcing consistency.
- Contextual Alignment methods, such as Retrieval-Augmented Generation (RAG) and Internet-enhanced techniques (e.g., IRCoT, ReAct), prepend retrieved documents or web content to prompts, compelling the LLM to align its generation with this external information and providing factual consistency [12,20]. RAG is a prominent method for leveraging external knowledge to handle new information and mitigate conflicts [30].
- Correction-based Alignment uses memory-enhanced methods that store feedback and revise LLM outputs if they contradict retrieved facts or user corrections [20].
- KnowPAT is a framework for knowledge-informed human alignment, leveraging domain-specific KGs to construct a “knowledge preference set” for fine-tuning LLMs, thereby aligning outputs with human knowledge and values [12].
- The
alignment agentwithinStructSenseexplicitly maps LLM-extracted entities to canonical counterparts in ontologies or KGs, providingknowledge groundingto mitigate ambiguities and minimizing the need for constant LLM fine-tuning for new domain knowledge [70]. KGValidatoraligns candidate triples with external textual documents, reference KGs (like Wikidata), and web search results to validate KG construction, demonstrating an implicit alignment of entities between the candidate triple and external sources [40].- In visual question answering,
DKAperforms knowledge alignment by disentangling complex questions into image-based and knowledge-based sub-questions, aligning retrieved external knowledge with visual context, and refining it through re-ranking based on image similarity [61].
General Knowledge Alignment and Fusion (KG-Centric): These techniques focus on reconciling knowledge from diverse structured sources.
- Entity Alignment aims to reduce redundancy by identifying synonymous entities across different KGs or languages [74]. Methods range from syntactic (e.g., string-based) and semantic (e.g., rule-based, subgraph-based) approaches to embedding-based techniques (sharing, swapping, mapping embedding spaces) [55].
- Knowledge Fusion combines information from multiple sources into a consistent, unified representation, addressing redundancy, inconsistency, contradiction, and granularity differences, with goals of completeness, conciseness, and correctness [55]. This often involves truth inferring strategies, such as source trustworthiness or probabilistic modeling, to determine true values among conflicting data. Models like
TDHandASUMSexplicitly address granularity differences, a common challenge where generic correct values are often treated as false, leading to information loss [55]. KnowMapemploys a fine-tuned knowledge-embedding model to align queries with relevant environmental and experiential knowledge bases using an InfoNCE loss, learning robust representations that capture cross-knowledge relationships [44].
Distinction: Synthetic Knowledge Ingestion for Model Enhancement vs. Evaluation
It is critical to differentiate between synthetic knowledge ingestion used for model enhancement/training and synthetic data generation employed for evaluation/measurement of knowledge utilization. While both involve creating artificial data, their purposes are distinct.
Synthetic knowledge ingestion for model enhancement directly contributes to improving an LLM’s capabilities or knowledge base. Examples include:
- The
Skiframework generating QA/QCA pairs for SFT or CPT [5]. - Fictional documents generated and ingested via fine-tuning to acquire new knowledge [60].
- Controlled synthetic factual knowledge used in continual pre-training to study knowledge acquisition under varying
knowledge entropyconditions, with the implicit goal of informing future enhancement strategies [34,69]. - Synthetic training examples for ontology evolution in
Evo-DKDto enable autonomous schema updates by LLMs [17]. - Meta-training sequences in metalearning frameworks, designed to train more capable learners rather than directly injecting facts into a fixed model [26].
- The “External Knowledge Memorization” mechanism in R1-Searcher++, where a rewriting model generates reasoning paths from retrieved documents, used to fine-tune a policy model to internalize knowledge for future use [27].
In contrast, synthetic data generation for evaluation or measurement focuses on probing an LLM’s existing knowledge or its acquisition mechanisms without directly aiming to augment its knowledge base. Examples include:
- The generation of fictional documents and associated Q&A pairs to study LLM memorization and knowledge acquisition processes, observing how LLMs integrate fictional facts with pre-existing knowledge [60].
- The use of a fictional knowledge dataset to assess an LLM’s ability to acquire and retain new knowledge under varying
knowledge entropyconditions [69]. - A stochastic “document generator” that creates synthetic documents for downstream retrieval tasks, allowing researchers to measure the knowledge acquisition-utilization gap in pretrained LMs by generating relevant and irrelevant documents based on factual triples [53].
- LLMs generating synthetic training data to aid in testing the performance of knowledge systems [52].
Challenges, Limitations, and Future Research
Despite significant advancements, both synthetic knowledge ingestion and alignment techniques face considerable challenges. A primary limitation for many SKI methods, particularly those leveraging KGs, is their tendency to focus on transforming a single raw knowledge source, often neglecting the complexities of mapping entities, reconciling schema differences, or ensuring semantic consistency when integrating knowledge from multiple, disparate KGs [1,5]. The reliance on distant supervision for KG-to-text verbalization introduces inherent noise, and the effectiveness of injection is ultimately dependent on the LLM’s ability to internalize the text [1].
For knowledge alignment, implicit ingestion methods suffer from well-documented issues like side effects and catastrophic forgetting, where new knowledge can interfere with existing knowledge, and the unreliability of parametric knowledge limits its propagation for reasoning and generalizability [20]. Explicit alignment methods, while mitigating some internal model modification risks, are susceptible to noisy and low-quality external content, which can lead to knowledge conflicts when LLMs prioritize internal knowledge over provided context [20]. The inherent semantic loss during input-layer injection (KG to text) and interference in intermediate-layer injection between textual and structural signals also pose significant hurdles [12].
A critical theoretical deficiency in existing KG alignment models is their assumption of deterministic knowledge, neglecting the uncertainty associated with entities and relations during matching [55]. Similarly, most KG fusion methods do not effectively handle granularity differences, often treating more generic correct values as false, leading to information loss. Furthermore, many fusion models primarily leverage source confidence, failing to account for confidence in extraction algorithms or pipeline components, which is problematic for long-tail entities or closely conflicting sources. Their specificity to numerical or categorical data further highlights the lack of a unified framework for mixed data types [55]. The “Knowledge Complexity Mismatch” further underscores that merely linking entities is insufficient; the quality and representational form of the ingested knowledge are paramount [7].
Future research should focus on several key areas to overcome these limitations. Firstly, developing robust alignment models that can explicitly incorporate and reason about uncertainty in entities and relations during the matching process is crucial [55]. Secondly, there is a pressing need for unified fusion models capable of simultaneously and robustly handling diverse data types (numerical, categorical, textual) and different levels of granularity within a single framework [55]. Thirdly, exploring the interaction between knowledge alignment techniques and knowledge entropy is essential to understand if specific alignment algorithms can mitigate the negative effects of knowledge entropy decay by efficiently integrating new knowledge into existing memory structures [69]. Finally, bridging the “cognitive gap” between LLM knowledge storage and human knowledge organization remains an overarching goal, requiring novel approaches to refine and inject knowledge such that it is not only factual but also semantically coherent and inferentially robust [12]. Further exploration into translating theoretical concepts like “social bootstrapping” into practical computational algorithms for dynamic LLM knowledge alignment could offer novel insights into robust knowledge integration [46]. Addressing these challenges will pave the way for more intelligent, adaptive, and trustworthy LLM systems.
5.2.3 Self-Tuning and Autonomous Knowledge Extraction
The pursuit of self-tuning and autonomous knowledge extraction aims to reduce dependency on explicit expert encoding and enable models to continuously learn and adapt to evolving information landscapes. This paradigm shifts the burden of knowledge acquisition from human curation to automated mechanisms, fostering model adaptability and scalability.
The Self-Tuning Paradigm and Spontaneous Knowledge Extraction in LLMs
Self-Tuning and Autonomous Knowledge Extraction Approaches
| Approach / Paradigm | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Self-Tuning Paradigm (LLMs) | LLMs “self-teach” by generating own learning tasks/signals. | Spontaneous knowledge acquisition, dynamic adaptation, scalability. | Self-Tuning framework (self-supervised, knowledge-intensive tasks). | Reliability of LLM-generated learning tasks, interpretability of strategies. |
| Spontaneous Knowledge Extraction | LLMs autonomously integrate new information from documents. | Reduces human intervention, adapts to evolving info. | R1-Searcher++ (internalizes retrieved info), AutoElicit (generates expert priors). | “Ineffective Utilization” of complex external knowledge, discernment issues. |
| LLM-Driven Ontology Evolution | LLMs autonomously update, maintain, and evolve knowledge bases. | Addresses manual ontology maintenance bottleneck, dynamic KB updates. | Evo-DKD (dual knowledge decoding, closed-loop updating). | Hallucination risk, ensuring consistency/accuracy, scalability for large ontologies. |
| Continuous KB Maintenance | Systems continuously extract, refine, and improve KBs. | Long-term adaptability, consistency, handles knowledge evolution. | NELL (Never-Ending Language Learner), SAC-KG (Verifier/Pruner modules). | Requires robust validation, computational cost, integration of external data. |
| Autonomous Knowledge Refinement | Optimizes and disentangles existing representations for utility. | Improves robustness, generalization, focuses on essential knowledge. | Pluvio (RL-based token pruning, CVIB for domain invariance). | Focuses on refinement, not new knowledge discovery, specific task optimization. |
| Recursive Bootstrapping | Iterative refinement of latent structures for efficiency. | Reduces computational complexity, stabilizes symbolic meaning. | Optimal Transport framework, Agent KB (experience abstraction). | Theoretical/heuristic, robust convergence analyses needed. |
| Learning Invariant Representations | Learning to “forget” nuisance information for robustness. | Enhances OOD generalization, disentangles semantics. | Conditional Variational Information Bottleneck (CVIB). | Requires identifiable “nuisance labels,” may lose subtle context. |
The core of the self-tuning paradigm in Large Language Models (LLMs) is the ability to “self-teach,” effectively instructing and training themselves to acquire new knowledge [68]. The Self-Tuning framework exemplifies this by employing a multi-stage training process. In its initial stage, an LLM learns how to absorb knowledge from plain text by generating its own self-supervised knowledge-intensive tasks, such as summarization, gist identification, and question answering [68]. These tasks are crucial for developing strategies for memorization, comprehension, and self-reflection. Uniquely, these learning tasks are “created in a self-supervised manner, without any mining patterns,” indicating that the LLM learns to generate its own learning signals internally [68]. In a subsequent stage, the LLM applies these learned strategies to “spontaneously acquiring knowledge from new documents” ($D_{test}^{Doc}$), integrating new information without further human intervention for task creation for these specific, unseen documents [68].
This capability for spontaneous knowledge extraction has significant implications for model adaptability and scalability. LLMs, by their nature, “contain knowledge themselves” and leverage “enormous web corpora to automatically construct rule bases using information extraction,” suggesting an inherent capacity for autonomous knowledge utilization [75]. The R1-Searcher++ framework, for instance, trains LLMs using reinforcement learning (RL) to “autonomously decide when to use its internal knowledge or to invoke an external retriever” [27]. This system further facilitates continuous internal enrichment through “External Knowledge Memorization,” allowing the model to internalize retrieved information and “progressively enrich its internal knowledge” for future self-reliant use [27]. Similarly, AutoElicit leverages the LLM’s pre-trained knowledge to generate expert priors and refines these priors based on incrementally detailed task descriptions, effectively performing spontaneous extraction and refinement of relevant information [19]. In general, LLMs exhibit implicit knowledge acquisition from vast internet-scale data, where training with error feedback provides “natural incentives” for emergent few-shot learning, multi-step reasoning, and compositional learning, allowing for spontaneous knowledge integration without explicit instruction for each new piece of information [26].
Despite these advancements, the effective integration of new knowledge remains a challenge. Critical assessments highlight that current LLMs often “fail to adequately disentangle the intricacy possessed in the external knowledge base,” treating aligned external knowledge “similarly to noise” [7]. This indicates a deficiency in their internal mechanisms for autonomous knowledge processing and refinement, suggesting that while they can absorb information, discernment and optimal integration are not guaranteed.
LLM-Driven Autonomous Ontology Evolution and Knowledge Base Maintenance
Beyond acquiring new facts, a critical aspect of autonomous knowledge management is the ability to maintain, update, and evolve knowledge bases (KBs) and ontologies. Evo-DKD provides a significant technical innovation in this area by enabling LLMs to “autonomously maintain, update, and evolve knowledge bases and ontologies” [17]. The underlying mechanism involves a “dual knowledge decoding” strategy within a closed reasoning loop. This loop allows proposed ontology edits to be validated and subsequently injected into the KB, informing future reasoning iterations and permanently recording new inferred knowledge [17]. This iterative self-updating process represents a form of closed-loop training where the model “is partly training itself over time as it ingests new data and modifies the knowledge base,” facilitating autonomous knowledge extraction and integration [17].
Precursors to LLM-driven ontology evolution include systems like NELL (Never-Ending Language Learner), which continuously extracts information from the web to populate and improve its KB over time [9,55]. NELL’s “Coupled Pattern Learner (CPL)” learns and refines extraction patterns incrementally, exhibiting autonomous extraction and self-teaching, though still requiring human validation [3]. The concept extends to agentic workflows, where LLMs can plan and orchestrate subtasks for knowledge extraction, dynamically adapting strategies to identify and integrate new knowledge from unseen documents [48]. LLMs’ capabilities in concept recognition and abstraction further enable “automated construction of conceptual hierarchies, ontological category expansion, attribute completion, ontology alignment, and concept normalization,” supporting autonomous ontology evolution [12]. Another approach for continuous knowledge management is seen in systems that autonomously generate, evaluate, and revise rules, deciding “what to forget,” “what to consolidate,” and “what to demote” based on metrics like Support, Optimality, and Permanence [67]. This allows KBs to evolve and refine themselves without constant manual intervention.
Challenges in automated knowledge base maintenance revolve around ensuring consistency, accuracy, and scalability. A significant concern with LLM-driven generative KG construction is the “risk of introducing incorrect knowledge (hallucination)” [12]. While systems like SAC-KG address this with a Verifier module to detect and correct errors and a Pruner to guide knowledge graph growth autonomously [66], the inherent reliability of LLM-generated facts without rigorous validation remains an issue [52]. Solutions often involve mechanisms like semantic quality filtering, where a separate model evaluates generated text to ensure only high-quality, non-hallucinated knowledge is integrated [1]. Scalability is also a concern, as highly autonomous systems, like Language Bottleneck Models (LBMs) employing Group Relative Policy Optimization (GRPO) for self-tuning, can be “computationally costly” and limited by “context length” [50].
Autonomous Knowledge Refinement and Domain Invariance
Autonomous knowledge refinement encompasses not only the acquisition of new information but also the optimization and disentanglement of existing representations to improve utility and robustness. While LLMs’ self-teaching mechanisms focus on acquiring and integrating new facts, other methods concentrate on achieving domain invariance in specialized applications.
Pluvio provides a compelling example of autonomous refinement in specialized PLM applications, particularly for achieving domain invariance [24]. It incorporates two key mechanisms:
Removalmodule (Reinforcement Learning Agent): This module acts as an autonomous token pruning mechanism, trained via a policy gradient algorithm to “eliminate noisy tokens from assembly code,” such as those from function inlining or compiler-injected code [24]. By learning to distinguish essential from redundant tokens, it refines input sequences for specialized tasks.- Conditional Variational Information Bottleneck (CVIB): This learning strategy enables the autonomous learning of invariant representations. During training, CVIB is conditioned on “nuisance labels” (e.g., architecture, optimization settings) to “forget” this irrelevant information [24]. The objective is to produce embeddings that are maximally informative about the learning target (e.g., semantic similarity) while minimizing information related to domain-specific factors that hinder out-of-domain generalization. This “forgetting” process is a sophisticated form of autonomous refinement, disentangling core functional knowledge from implementation details [24].
This contrasts with the Self-Tuning framework’s goal of acquiring new explicit knowledge into LLM parameters, as Pluvio focuses on refining internal representations and processing for specific tasks to achieve robustness across different domains, rather than discovering new knowledge per se.
Other methods contribute to autonomous refinement through various theoretical foundations and architectural choices:
- Recursive Bootstrapping: This self-refining process, described in the context of information bottleneck, guides the iterative refinement of latent structures by minimizing conditional entropy. It leads to the convergence of compact, low-entropy latent structures and signifies a self-tuning process for symbolic meaning stabilization through “delta convergence” [46].
- Self-Supervised Learning: By formulating “pretext tasks” where labels are automatically provided, self-supervised learning enables models to extract meaningful information autonomously from raw data, fostering skill-invariant models without direct human annotation [47].
- Latent Space Refinement: In systems like
Latplan, unsupervised learning in State Autoencoders (SAEs) identifies relevant features, and a non-standard Bernoulli prior acts as an autonomous refinement mechanism to encourage sparsity and filter out uninformative features in the latent space [28]. - Iterative Optimization: The variational EM algorithm in
KRDLiteratively refines uncertain formula weights for weak supervision and improves prediction models, acting as a self-tuning mechanism for denoising and knowledge integration [16]. - Reinforcement Learning for Refinement: The encoder in LBMs is optimized via GRPO, an RL algorithm, to iteratively generate and refine natural-language summaries based on a reward function, improving its ability to capture knowledge states and misconceptions [50].
- Adaptive Elicitation: Mechanisms to “actively reduce uncertainty” about “new, unseen, latent entities” by systematically sharpening beliefs based on observed question-answer pairs represent an autonomous refinement process for specific knowledge acquisition [13].
Many “autonomous” systems, however, operate within constraints, requiring initial human definition of patterns (e.g., EneRex for weakly-supervised data generation [51]) or predefined search spaces and objectives (e.g., CEGA for adaptive node selection in GNNs [45], AutoPrompt for eliciting existing knowledge via automated prompt generation [43]). These approaches automate processes but often fall short of truly spontaneous, unsupervised discovery of new knowledge or learning strategies.
Limitations and Future Research
Despite significant strides, fully autonomous knowledge acquisition and self-tuning mechanisms face several inherent limitations. The hallucination problem in LLMs poses a fundamental reliability challenge, limiting their autonomous operation without human oversight [12]. Computational costs and context length limitations, as noted in LBMs, restrict the practical scalability of some advanced self-tuning methods [50]. Furthermore, many systems, even those termed “autonomous,” retain a degree of data dependency or rely on predefined rules and schemata, limiting their ability to discover entirely novel knowledge types or adapt to fundamentally new domains without explicit guidance [43,44].
Future research needs to address these challenges by exploring mechanisms for robustly identifying and integrating new, correct knowledge without human intervention. This includes developing advanced error detection and self-correction capabilities within LLMs themselves, moving beyond external verifiers. Research into truly unsupervised discovery of emergent knowledge from diverse, unstructured data streams remains crucial. Integrating modalities beyond text, and enabling continuous, lifelong learning where models can autonomously prioritize, weigh, and forget information to maintain a manageable and accurate knowledge base, are vital next steps [37]. Ultimately, overcoming the “Knowledge Acquisition/Utilization Gap,” where LLMs struggle to adequately disentangle complex external knowledge [7], is paramount for realizing the full potential of self-tuning and autonomous knowledge extraction.
5.3 Learning and Optimization Algorithms
Addressing the Knowledge Acquisition Bottleneck (KAB) fundamentally relies on advanced learning and optimization algorithms that govern how intelligent systems acquire, refine, transfer, and manage knowledge. These algorithms are critical for enabling efficient data utilization, accelerating model development, and ensuring the adaptive evolution of knowledge in dynamic environments. Across diverse domains, from natural language processing to robotics and game AI, researchers have developed specialized techniques to optimize various aspects of the knowledge lifecycle, each characterized by distinct underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations.
A primary strategy for efficient knowledge acquisition focuses on optimizing data utilization through iterative and active sampling. Active Learning (AL) algorithms employ various acquisition functions, such as uncertainty sampling, to select the most informative samples for labeling, thereby minimizing annotation costs and the dependency on extensive labeled datasets [57]. Common acquisition functions include Least Confidence (LC) and Maximum Length-Normalized Log Probability (MNLP), which prioritize samples where the model’s confidence is lowest or its entropy is highest [15,57]. To capture more complex model uncertainty, Bayesian Active Learning by Disagreement (BALD), often combined with Monte Carlo Dropout (DO-BALD) or Bayes-by-Backprop (BB-BALD), quantifies epistemic uncertainty by measuring the disagreement among multiple stochastic predictions [57]. These methods are not limited to data annotation but also extend to model extraction, using strategies like K-center for diversity or adversarial approaches (e.g., DeepFool Active Learning) for identifying decision-boundary instances [15]. In robotics, acquisition functions implicitly guide exploration, as seen in InfoBot’s use of KL divergence to prioritize “decision states” for knowledge gain, often complemented by count-based visitation bonuses for novel state exploration [56,64]. The core idea is to iteratively refine a model’s understanding by strategically querying for samples that offer the greatest information gain, often measured by metrics such as Expected Information Gain (EIG) [13].
Iterative refinement and bootstrapping algorithms are central to generating and transforming knowledge representations. Recursive bootstrapping algorithms, particularly theorized in contexts like Optimal Transport, iteratively refine internal representations through a fixed-point process where an update rule, $\Phi^{(t+1)} = \mathcal{F}(\Phi^{(t)}, \Psi^{(t)})$, ensures entropy minimization and convergence to generalization-optimal latent states [46]. This reduces computational complexity and leads to sharply peaked distributions over latent content. Practically, bootstrapping manifests in various forms: Self-Tuning’s self-supervised generation of knowledge-intensive tasks from raw documents [68], SAC-KG’s entity-induced tree search for iterative knowledge graph expansion [66], and Agent KB’s abstraction of human-annotated failure cases for generalizable problem-solving [33]. In game AI, convex optimization plays a crucial role in concept discovery, as demonstrated by AlphaZero where it extracts sparse concept vectors from latent representations by minimizing the $L_1$ norm subject to constraints derived from optimal and suboptimal game trajectories, thereby making implicit AI knowledge interpretable [54]. For student knowledge sharing, bi-level optimization dynamically adjusts student importance weights ($\omega$) using Mirror Descent in an outer loop, while an inner loop optimizes network parameters ($\theta$) via AdamW, enabling effective peer-to-peer knowledge distillation and refinement [8]. Policy search algorithms, such as Natural Actor-Critic (NAC) and Policy Learning by Weighting Exploration with the Returns (PoWER), optimize reward functions in robotics to refine learned behaviors, often starting from “warm starts” provided by imitation learning [64]. Algorithms for unsupervised skill discovery, like IBOL, utilize policy gradient methods and the information bottleneck principle to learn expressive and transferable latent skill representations [35]. Finally, RL-based token pruning, as implemented in Pluvio’s Removal module, optimizes a reward function $R = \frac{1}{L_{\mathrm{cos_sim}}}$ using policy gradients to select the most semantically relevant tokens, effectively minimizing noise and focusing on critical elements for robust representation learning in assembly code analysis [24].
Network architecture and parameter transfer techniques are vital for accelerating learning and reducing data dependency by leveraging existing knowledge. Net2Net techniques, comprising Net2WiderNet and Net2DeeperNet, enable dynamic network modification by transferring knowledge from a previous network to a new, modified one [62]. Net2WiderNet expands a layer by copying existing weights and distributing them proportionally, while Net2DeeperNet inserts new layers initialized to perform identity functions. This allows larger networks to build upon fully trained smaller networks without training from scratch. This approach is distinct from recursive bootstrapping; while both involve iterative refinement, Net2Net focuses on architectural evolution and direct parameter mapping for scaling, whereas recursive bootstrapping, as seen in Optimal Transport, is a more abstract meta-strategy for iterative refinement of internal representations through fixed-point dynamics. Transfer learning, particularly fine-tuning pre-trained language models (PLMs), is a widespread parameter transfer paradigm, adapting general knowledge from massive text corpora to specific downstream tasks [38]. Conditional Variational Information Bottleneck (CVIB), used in Pluvio, extends this by explicitly disentangling desired information from nuisance factors (e.g., architectural specifics) to achieve domain-invariant representations, effectively “forgetting” irrelevant contextual details during learning [24]. Parameter-Efficient Fine-Tuning (PEFT) methods, such as LoRA and Adapters, reduce the computational burden of fine-tuning large models by updating only a small subset of parameters, efficiently adapting pre-trained knowledge [73]. Knowledge distillation further allows transferring knowledge from larger “teacher” models to smaller “student” models, or even among diverse student models in approaches like Diversity Induced Weighted Mutual Learning (DWML) [8].
Effective knowledge acquisition in continuous learning systems also necessitates sophisticated forgetting and consolidation algorithms to manage the inherent stability-plasticity dilemma. These algorithms dictate how systems retain crucial information while integrating new knowledge and discarding outdated or irrelevant data [67]. Frameworks utilize MML-derived metrics to define explicit procedures for “forgetting” (removing low-informativeness rules), “consolidation” (promoting robust rules to long-term memory), and “demotion” (reverting rules to working memory or discarding them) [67]. For LLMs, mitigating catastrophic forgetting is critical. Solutions include data replay interventions to reactivate knowledge circuits [34], regularization-based methods (e.g., RecAdam) to preserve critical parameters [20], and architectural methods (e.g., K-Adapter, LoRA) that freeze original parameters while adapting new knowledge through lightweight modules [20]. The observed decay of knowledge entropy during pre-training, which hinders new knowledge acquisition, can be counteracted by a “resuscitation algorithm” that increases the activity of previously inactive memory vectors [69]. In KnowMap, an external environmental knowledge base employs a replacement mechanism for factual updates, while SAC-KG’s Verifier and Pruner modules filter irrelevant information during KG construction, ensuring selective consolidation [44,66]. R1-Searcher++ explicitly optimizes LLMs to internalize retrieved external knowledge, transforming it into persistent memory through a “Knowledge Memorization Loss” [27]. These mechanisms are crucial for lifelong learning systems, especially in robotics, where continuous adaptation to dynamic environments requires implicitly “forgetting” outdated models of body dynamics and “consolidating” new behaviors to ensure robust operation [64].
Despite significant advancements, several challenges persist in learning and optimization algorithms for knowledge acquisition. Computational cost and scalability remain major limitations, particularly for iterative AL loops, bi-level optimization, reinforcement learning, and fine-tuning large language models [8,20,57]. Many bootstrapping and optimization strategies are highly domain-specific, lacking rigorous theoretical guarantees or extensive analysis of their generalizability across different contexts [46,64]. The assumption of a “quasi-static knowledge state” in many models restricts their adaptability to dynamic, real-world scenarios [3,50]. Furthermore, the effectiveness of knowledge transfer can be hindered by architectural mismatches or semantic loss during knowledge injection, leading to ineffective knowledge utilization [7,12].
Future research should focus on developing more computationally efficient and theoretically robust recursive bootstrapping and optimization algorithms, particularly those that can dynamically adapt to evolving knowledge and leverage implicit knowledge representations in deep latent spaces without explicit labels. There is a critical need for novel multi-objective optimization algorithms that balance correctness, completeness, and granularity in knowledge acquisition pipelines within dynamic and uncertain environments [55]. Enhancing the interpretability of learned and transferred knowledge, especially in LLMs, and bridging the gap between theoretical frameworks and large-scale practical implementations are also vital. Finally, reducing the manual effort in defining reward functions, acquisition strategies, and architectural constraints, possibly through meta-learning or automated discovery, could significantly improve the scalability and applicability of these powerful KAB-attacking techniques.
5.3.1 Acquisition Functions and Uncertainty Estimation (Active Learning)
Active Learning (AL) represents a crucial strategy for attacking the knowledge acquisition bottleneck by optimizing data selection, thereby reducing the dependency on extensive labeled datasets [57]. The core principle of AL revolves around the intelligent selection of the most informative samples for labeling, guided by acquisition functions that leverage uncertainty estimates from a predictive model. This process is inherently iterative, where a model is trained on a small labeled dataset, its uncertainty over unlabeled data is estimated, and the most uncertain (or informative) samples are queried for human annotation, progressively refining the model [4,57].
Common acquisition functions predominantly rely on uncertainty sampling, where samples about which the current model is least confident are selected.
Active Learning Acquisition Functions for KAB
| Acquisition Function Category | Core Mechanism | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Confidence-Based Ranking | Selects instances with low confidence scores. | Prioritizes uncertain samples for review/re-annotation. | Least Confidence (LC), Max Length-Normalized Log Probability (MNLP). | Primarily captures aleatoric uncertainty, may miss epistemic uncertainty. |
| Entropy-Based Sampling | Selects instances with high entropy in predicted probabilities. | Prioritizes uncertain samples, ensures diverse exploration. | Entropy ($\mathcal{H}_n$), used in model extraction (CEGA). | Sensitive to outliers, computational cost for large prediction spaces. |
| Bayesian Active Learning by Disagreement (BALD) | Measures disagreement among multiple stochastic predictions. | Quantifies epistemic uncertainty, more comprehensive view of model uncertainty. | DO-BALD (Monte Carlo Dropout), BB-BALD (Bayes-by-Backprop). | Computationally expensive, requires stochastic models. |
| Expected Information Gain (EIG) | Quantifies expected reduction in entropy about target variable. | Guides query selection for optimal information gain. | EIG for adaptive elicitation (e.g., student skill assessment). | Computationally intensive to calculate, relies on accurate model of information. |
| Expert Suitability Scoring | Estimates expert’s relevance/cost for a given question. | Optimizes human expert engagement under budget constraints. | PU-ADKA (Positive-Unlabeled learning for question-expert matching). | Requires reliable expert models, complex optimization. |
| Diversity-Based Sampling | Selects samples maximally distant from existing clusters. | Ensures broad coverage of input space, avoids redundant queries. | K-center strategy (in model extraction). | Can be computationally intensive, defining “distance” is crucial. |
| Adversarial Sampling | Identifies samples near decision boundaries via perturbations. | Efficiently probes model boundaries, effective for model extraction. | DeepFool Active Learning (DFAL). | Computationally expensive, relies on adversary’s model, can be detected. |
| RL-Guided Exploration | Uses intrinsic rewards to guide agents to informative states. | Reduces need for dense external rewards, learns task structure. | KL divergence in InfoBot (for “decision states”), count-based bonuses. | Designing effective reward functions, sample inefficiency. |
A fundamental approach involves confidence-based ranking, selecting instances with lower confidence scores for review or re-annotation [6,25]. For instance, in Named Entity Recognition (NER), models trained on initial data generate confidence scores, and sentences with lower scores are prioritized for human review to fix errors, demonstrating effectiveness in data quality improvement [25]. Similarly, in Knowledge Graph (KG) construction, human-in-the-loop (HIL) systems implicitly query for samples where confidence is low or ambiguity is high, accepting annotations based on a confidence threshold [3]. The StructSense framework also employs a judge agent that assigns confidence scores to extracted outputs, serving as an internal uncertainty estimation that could guide human intervention, although not explicitly formalized as an AL acquisition function for strategic sample selection [70].
| More formally, Least Confidence (LC) selects the example $x$ for which the model’s highest predicted probability for any class is the lowest, minimizing $\max_y P(y | x)$ [57]. For sequence labeling tasks, Maximum Length-Normalized Log Probability (MNLP) normalizes this by sequence length to prevent bias towards longer sequences [57]. Another prevalent uncertainty measure is entropy, which quantifies the predictability of the model’s output distribution. Samples with higher entropy, indicating greater uncertainty, are prioritized for labeling. This is mathematically expressed as $\mathcal{H}n = - \sum{j} \tilde y_{n,j} \log \tilde y_{n,j}$ [15], and has been successfully applied in graph-based model extraction for selecting informative nodes [45]. These classical uncertainty sampling methods primarily capture aleatoric uncertainty (noise inherent in the data), but often overlook epistemic uncertainty (the model’s uncertainty due to limited knowledge), which can lead to suboptimal sample selection [57]. |
To address epistemic uncertainty, Bayesian Active Learning by Disagreement (BALD) is employed, which selects samples where multiple stochastic forward passes through the model disagree most with the plurality opinion [57]. This can be combined with uncertainty estimation methods such as Monte Carlo Dropout (DO-BALD), where dropout is kept active during prediction to generate multiple stochastic outputs, and Bayes-by-Backprop (BB-BALD), which models weights as probability distributions and samples from them to quantify uncertainty [57]. These Bayesian approaches provide a more comprehensive view of model uncertainty. Another method to gauge uncertainty is perturbation-based analysis, where samples whose predicted labels change significantly under small perturbations are considered more uncertain and informative, particularly useful for identifying nodes near decision boundaries in graph-based models [45].
Beyond simple uncertainty, acquisition functions can incorporate other criteria to maximize information gain. Expected Information Gain (EIG) explicitly quantifies the expected reduction in entropy about a target variable after observing a new question-answer pair, actively guiding the selection of queries to reduce overall model uncertainty [13]. In the context of LLMs, a novel acquisition function within the PU-ADKA framework estimates an “expert suitability” score using Positive-Unlabeled (PU) learning, $g(q_i, e_j)$, to guide the selection of question-expert pairs for annotation. This emphasizes optimizing expert engagement in sensitive domains, a domain-specific adaptation to traditional AL [4].
Active learning principles extend beyond data labeling to tasks like model extraction and robotics exploration. In adversarial model extraction, AL acquisition functions are utilized to minimize query costs when stealing a secret model. Strategies include uncertainty sampling (entropy), K-center strategy for diversity by selecting samples most distant from existing cluster centers to cover the output space, and Adversarial Strategy (DeepFool Active Learning - DFAL), which identifies samples near decision boundaries by finding minimum perturbations to change their classification [15]. These can be combined, such as the Adversarial+K-center ensemble strategy, to filter informative samples and ensure diversity [15]. The efficiency of these methods is crucial as querying a secret model is costly. Similarly, CEGA also applies entropy-based and perturbation-based uncertainty for graph-based model extraction, highlighting the importance of cost-effective acquisition [45].
In robotics, active learning acquisition functions relate to exploration strategies and uncertainty management, paramount for safety and efficient data collection in physical systems [64]. While not always explicitly termed AL, learned behaviors often implicitly handle uncertainty from noisy sensor data. For instance, robots can adapt motions to compensate for imperfect state estimation, learn uncertainty-aware collision avoidance by outputting collision probabilities and their uncertainties, and reduce pose estimation uncertainty by trading off accuracy and speed [64]. The InfoBot framework implicitly uses KL divergence as an acquisition function for exploration, guiding agents to prioritize “decision states” where action choice is highly goal-dependent and thus most informative for knowledge gain, often combined with count-based terms to promote visiting less explored states [56]. This emphasizes acquiring knowledge about task structure and environmental dynamics.
Several approaches implicitly use “acquisition” mechanisms without explicit AL definitions. The R1-Searcher++ framework allows LLMs to autonomously decide whether to use internal knowledge or an external retriever, functioning as an implicit acquisition strategy where internal uncertainty triggers external information retrieval [27]. Bayesian Optimization, used for architectural search in student models, employs an implicit acquisition function to efficiently guide the search for hyperparameters by minimizing the difference between actual and target parameters [8]. Even gradient-guided search for trigger tokens in prompt engineering acts as an optimization for prompt acquisition, aiming to maximize the likelihood of correct predictions by selecting informative prompt elements, though distinct from data annotation [43].
Despite these advancements, limitations and areas for improvement persist. Many systems that implicitly leverage active learning principles, such as those in KG construction or LLM knowledge acquisition, often lack formal specification of acquisition functions or detailed uncertainty estimation methods [3,37,72]. The computational expense of advanced uncertainty quantification, like DFAL or Bayes-by-Backprop, remains a challenge, particularly in iterative AL loops [15,57]. Furthermore, uncertainty estimates in model extraction often rely on a substitute model, which may not accurately reflect the secret model’s uncertainty, particularly in early iterations [15]. Future research should focus on integrating more sophisticated and computationally efficient uncertainty quantification methods (e.g., ensemble disagreement), formalizing implicit acquisition strategies, and exploring hybrid approaches that combine different acquisition criteria (uncertainty, diversity, relevance) to address the data scarcity and annotation bottleneck more effectively across diverse domains [20,55].
5.3.2 Optimization and Bootstrapping Algorithms
The efficient acquisition, generation, and refinement of knowledge are pivotal to overcoming the Knowledge Acquisition Bottleneck (KAB). This often necessitates sophisticated optimization and bootstrapping algorithms that can transform limited initial information into more comprehensive or semantically rich representations. These techniques leverage iterative processes, self-supervision, and various objective functions to enhance learning and model capabilities across diverse domains.
Optimization and Bootstrapping Algorithms for KAB
| Algorithm Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Recursive Bootstrapping | Iteratively refines internal representations towards a fixed point. | Reduces computational complexity, converges to generalization-optimal states. | Optimal Transport (entropy minimization), Self-Tuning (self-supervised tasks), Evo-DKD (ontology updates). | Theoretical, convergence analyses needed, often heuristic in practice. |
| Latent Space Learning | Acquires symbolic/functional knowledge within latent spaces. | Enables implicit knowledge discovery, reduces explicit modeling. | BTL (STRIPS semantics from neural nets), AXCELL (ULMFiT). | Symbol Stability Problem, uniform sampling issues, interpretability of latents. |
| Bi-level Optimization | Nested optimization loops (inner: model params, outer: meta-params). | Dynamically adjusts importance weights, facilitates peer-to-peer knowledge distillation. | DWML (dynamic student weighting). | High computational overhead, complexity of nested optimization. |
| LLM Internal Refinement | Mechanisms for fine-tuning LLM internal knowledge structures. | Improves efficiency of knowledge circuits, increases plasticity. | Knowledge circuit optimization, Resuscitation algorithm (knowledge entropy). | Linear scaling for resuscitation, limited to specific LLM components. |
| Iterative Refinement | Continuous process of improving knowledge/policies. | Enhances robustness, adaptivity, and accuracy. | Policy search (NAC, PoWER in robotics), AlphaZero (concept discovery, student AI training), Pluvio (RL-based token pruning). | Domain-specific, limited generalizability, computationally costly. |
| Reinforcement Learning (RL) Optimization | Optimizes policies via reward signals for sequential decision-making. | Efficient exploration, dynamic knowledge acquisition, skill discovery. | GRPO (GRAIL, LBMs), REINFORCE++ (R1-Searcher), Double DQN (PU-ADKA), Policy Gradients (IBOL). | Designing effective reward functions, sample inefficiency, computational cost. |
| Constraint-Driven Learning | Embeds symbolic constraints or rules into loss functions. | Ensures scientific coherence, adherence to domain expertise. | MatSKRAFT (physicochemical constraints for table extraction). | Defining constraints, balancing with data-driven learning. |
| Active Learning (Iterative) | Iterative querying to refine model understanding. | Optimizes data acquisition, reduces annotation effort. | CEGA (GNN acquisition), Model Extraction (substitute models), targeted re-annotation. | Computational expense of retraining, oracle reliability. |
| Standard Optimizers | Algorithms for gradient-based parameter updates. | Efficiently tunes model parameters. | AdamW, SGD, AdaGrad (for KBC). | Requires large datasets, hyperparameter tuning. |
| Recursive bootstrapping algorithms are fundamental to iteratively refining knowledge representations. In the context of Optimal Transport (OT), a theoretical framework proposes recursive entropy minimization as a bootstrapping mechanism that yields structured memory states converging to delta-like distributions over latent manifolds [46]. The update rule, $\Phi^{(t+1)} = \mathcal{F}(\Phi^{(t)}, \Psi^{(t)})$, where $\mathcal{F}$ is a contractive refinement operator, is theoretically proven to be entropy-decreasing, leading to a unique fixed point $\Phi^*$ that minimizes long-term contextual uncertainty and provides a generalization-optimal latent representation. This approach significantly reduces inference complexity from $\mathcal{O}(\exp(D))$ to $\mathcal{O}(k^2)$ by projecting high-dimensional contexts onto low-dimensional structured representations, utilizing an objective function $\mathcal{L}(\Phi) = H(\Psi | \Phi) + \lambda D_{\mathrm{OT}}(p(\Psi | \Phi), \nu)$ where $D_{\mathrm{OT}}$ is the optimal transport cost [46]. This theoretical grounding posits bootstrapping as a meta-strategy for sequential refinement. Related practical implementations of bootstrapping include Self-Tuning’s self-supervised generation of diverse knowledge-intensive tasks from raw documents [68], EneRex’s seed word expansion and pattern-based sentence selection for weakly-supervised data generation [51], and SAC-KG’s entity-induced tree search that iteratively generates and refines domain knowledge graphs [66]. Similarly, Agent KB uses human-annotated failure cases as few-shot examples to prompt an LLM-based experience generator, bootstrapping an abstraction process for generalizable problem-solving [33]. The Evo-DKD framework also employs a closed reasoning loop where validated ontology updates continuously refine the LLM’s knowledge base, demonstrating iterative refinement in autonomous ontology evolution [17]. |
Learning in a latent space can significantly alleviate the KAB in classical planning by enabling models to discover and utilize planning knowledge without explicit action labels [28]. The Back-to-Logit (BTL) mechanism transforms neural network operations to enforce STRIPS semantics, allowing knowledge of action effects and preconditions to be implicitly acquired and represented within deep latent spaces. The Complete State Regression Semantics casts precondition learning as an inverse effect learning problem, optimizing the completeness and fidelity of the learned action model by directly extracting conjunctive preconditions from network weights. This architectural choice inherently resolves the KAB by enabling symbolic knowledge extraction from an otherwise opaque deep learning model, but its “bootstrapping” aspect is more about architectural design than iterative model improvement or data generation [28]. AXCELL demonstrates implicit knowledge acquisition in latent spaces through ULMFiT’s pre-training on large text corpora, forming internal representations that encode contextual knowledge for downstream tasks like table classification and segmentation [41].
For dynamically learning student weights in knowledge sharing, a bi-level optimization algorithm has been proposed [8]. The inner loop involves updating multiple student models’ parameters ($\theta$) simultaneously using AdamW gradient descent, minimizing a combined loss of cross-entropy (supervision from labels) and KL divergence (peer supervision). This enables each student to learn from the soft logits of others, effectively bootstrapping knowledge refinement from evolving peer states. The outer loop dynamically adjusts the importance weights ($\omega_i$) of peer models using mirror descent, ensuring that more capable students contribute proportionally more to the mutual learning process. This iterative, dynamic weighting system transforms initial, diverse student models into a more refined collective understanding, validated by a positive correlation between learned importance weights and model performance (R=0.7) [8]. However, this sophisticated optimization scheme comes with a higher computational overhead [8].
The “optimization phase” of knowledge circuits in Large Language Models (LLMs) relates to internal model refinement [34]. Following an initial “formation phase” where critical knowledge structures emerge, the optimization phase sees a slower, continuous decrease in knowledge circuit entropy, refining existing structures for efficiency. This suggests an inherent bootstrapping-like mechanism within LLMs, where initial knowledge representations are recursively enhanced. Complementing this, a “resuscitation algorithm” broadens the distribution of active memory coefficients in LLM Feed-Forward Networks, aiming to increase knowledge entropy and make the model more receptive to new information during continual learning. This involves a heuristic parameter scaling process (Algorithm 1) where weights in the up-projection matrix $K_l$ are multiplied by $u = \frac{\text{mean}(C_l)}{C_l} \times q$ based on average memory coefficients, resuscitation ratio ($p$), and an amplifying factor ($q$) [69]. While effective in improving knowledge acquisition and reducing forgetting in later pre-training stages, this linear scaling lacks the complexity of more sophisticated recursive knowledge generation mechanisms [69].
Iterative refinement processes, while conceptually similar, manifest distinctly across different domains to address specific KABs. In robotics, bootstrapping techniques prioritize safety and data efficiency. Learning often initiates in controlled environments or simulations, reducing real-world interaction needs and inherent safety risks [64]. Guiding policies or safety mechanisms, such as collision avoidance, allow for safe exploration and data collection, which then refine learned behaviors. Imitation learning provides a “warm start” by initializing policies from human demonstrations, simplifying subsequent reinforcement learning tasks [64]. Specific optimization algorithms like NAC and PoWER are then used to iteratively refine these policies to maximize reward functions. InfoBot’s policy gradient optimization, incorporating an intrinsic reward based on KL divergence, also bootstraps learning in sparse reward environments by identifying “decision states,” transforming sensory input into structural knowledge for exploration and transfer between tasks [56]. Similarly, the “linearizer” in unsupervised skill discovery simplifies environment dynamics, offering a stable and efficient base for learning diverse skills, which acts as a bootstrapping mechanism [35].
| Conversely, in game AI, the focus shifts to explicit concept discovery and transfer from implicit latent spaces. AlphaZero employs convex optimization to discover sparse concept vectors by minimizing the $L_1$ norm of the concept vector ($ | \mathbf{c} | _1$) subject to linear constraints. These constraints are derived by contrasting latent representations from optimal and suboptimal Monte Carlo Tree Search (MCTS) rollouts, effectively transforming patterns in the AI’s behavior into semantically rich concepts [54]. This allows for the extraction of implicit knowledge even when explicit action labels are unavailable. For knowledge transfer, a student AI is bootstrapped through curriculum learning, trained on a small, curated set of concept “prototypes,” achieving performance gains comparable to thousands of self-play epochs through KL divergence minimization and the Adam optimizer [54]. This contrasts sharply with robotics, where bootstrapping primarily facilitates data collection and policy initialization, versus explicit concept extraction in game AI. |
For semantic token pruning and noise reduction in assembly code, Pluvio utilizes an RL-based optimization for its Removal module [24]. This involves a one-step RL agent with a reward function $R = \frac{1}{L_{\mathrm{cos_sim}}}$ and a policy gradient for optimization. The objective is to select the top-$k$ tokens based on their probability distribution, thereby reducing sequence length and removing noisy information stemming from compiler artifacts like function inlining and injected code. This optimization directly addresses KAB by ensuring that the input representation focuses on critical elements, enhancing effective sequence length for analysis in out-of-domain architectures and libraries [24].
Beyond these specific domain applications, various other optimization and bootstrapping strategies contribute to mitigating the KAB. The InfoNCE objective, while a powerful optimization for representation learning, is specifically highlighted in measuring_the_knowledge_acquisition_utilization_gap_in_pretrained_language_models for fine-tuning to measure knowledge utilization in a downstream task rather than as a general KAB-attacking optimization algorithm. Its loss function:
\(\mathcal{L}(k) = -\log \frac{\exp(\mathrm{sim}(q, d^+))}{\sum_{d \in \{d^+,d^-_1,\dots,d^-_m\}} \exp(\mathrm{sim}(q, d))}\)
drives the model to optimize its ability to retrieve correct documents based on internal knowledge during evaluation [53]. In contrast, KnowMap explicitly uses the InfoNCE loss function for fine-tuning a knowledge-embedding model to learn representations where task-relevant knowledge is maximally similar to queries, serving as a direct KAB-attacking optimization for retrieval [44].
Reinforcement Learning (RL) based optimizations are prevalent. GRAIL employs Group Relative Policy Optimization (GRPO) to enhance LLM-based retrievers for graph comprehension and reasoning, utilizing Process-based Reward Models (PRMs) for granular per-step reward signals to address sparsity and improve credit assignment in complex graph retrieval [63]. LBMs also use GRPO for encoder optimization, aiming to balance reconstruction accuracy, predictive accuracy, and summary conciseness for interpretable knowledge tracing [50]. The R1-Searcher framework employs the REINFORCE++ algorithm, guiding dynamic knowledge acquisition through a reward function that balances internal knowledge use and external retrieval, further supported by recursive knowledge refinement through external knowledge memorization [27]. Another RL application is in Multi-Agent Reinforcement Learning (MARL) for active domain knowledge acquisition, using a Double DQN architecture for efficient selection of question-expert pairs and bootstrap sampling to enhance generalization [4].
Constraint-driven learning acts as an optimization for knowledge generation by guiding models towards scientifically coherent interpretations. MatsKraft, for instance, defines structural constraints (e.g., material-property association) and incorporates them into a total loss function, $\mathcal{L}{\text{total}} = \mathcal{L}{\text{CE}} + \lambda \cdot \mathcal{L}{\text{constraint}}$, where $\mathcal{L}{\text{constraint}}$ is computed by summing ReLU-activated violations, acting as “soft rules” to optimize knowledge extraction from scientific tables [65].
Iterative refinement and active learning strategies are widely used for bootstrapping. CEGA uses iterative training and selection of labeled nodes to bootstrap a GNN model’s understanding of a target GNN’s behavior, maximizing performance and resemblance with minimized query budget [45]. A model extraction framework similarly uses active learning in an iterative process to train and refine a substitute model by continuously feeding it informative data points from a secret model, thus bootstrapping knowledge of decision boundaries [15]. For improving data quality, single_versus_multiple_annotation_for_named_entity_recognition_of_mutations proposes an iterative optimization cycle where machine learning models bootstrap the identification of erroneous examples for targeted re-annotation, significantly reducing the performance gap with minimal manual effort [25]. StructSense employs a multi-agent architecture with a feedback loop for iterative refinement and self-correction, using shared memory to bootstrap improvements in structured information extraction [70]. AutoPrompt implements an iterative optimization for trigger token selection in LLMs, using gradient-guided candidate selection and greedy search to bootstrap task-specific prompts that efficiently probe implicit knowledge [43].
Standard optimizers like AdamW, SGD, and AdaGrad are foundational. AdamW is frequently employed for fine-tuning LLMs across various tasks, from generative KG completion [49] to synthetic knowledge ingestion [5], with AdaGrad specifically noted for its effectiveness in Knowledge Base Completion (KBC) for link prediction due to its adaptive learning rate [9]. Net2Net serves as a bootstrapping mechanism for training larger neural networks by transferring knowledge from smaller, pre-trained models via weight copying and identity initialization, accelerating convergence compared to random initialization [62].
In Knowledge Graph construction, optimization often targets scalability and efficiency. Techniques like MinHash/LSH blocking, summarization, and parallel execution optimize scalable entity resolution, while NELL’s Coupled Pattern Learner iteratively refuses extraction capabilities. SPARQL-CONSTRUCT offers knowledge generation through query optimization, and SAGA optimizes incremental KG updates through parallel batch jobs [3]. Within uncertain KG embedding, models like GTransE, IIKE, and UOKGE optimize loss functions such as margin loss, logarithmic probabilities, and mean squared error to incorporate uncertainty into knowledge representations [55]. Iterative truth discovery methods, often employing Expectation-Maximization (EM) algorithms, iteratively refine estimates of source trustworthiness and fact veracity [55]. NELL itself acts as a continuous learning system that bootstraps knowledge acquisition by iteratively extracting, refining, and classifying facts [55].
Meta-learning approaches also contribute to KAB mitigation by optimizing the learning process itself. Frameworks that metalearn entire learning dynamics or train to become proficient at learning new tasks from demonstrations essentially bootstrap the model’s ability to learn, representing a higher-order optimization [26]. This recursive mechanism enables the meta-learner to acquire knowledge more efficiently across diverse tasks. Similarly, in continual learning, meta-training can optimize models for faster adaptation to new knowledge streams by reweighting token losses [20].
LLM-specific bootstrapping and optimization strategies are becoming increasingly sophisticated. Instruction fine-tuning uses task-specific instructions to bootstrap LLMs’ generalization ability, while advanced prompt engineering (e.g., Chain of Thoughts, Tree of Thoughts) iteratively optimizes input to guide higher-level reasoning. Reward model training frameworks like KnowPAT leverage KGs to inform reinforcement learning, aligning LLMs with human knowledge and preferences. Distant supervision from KGs effectively bootstraps large labeled datasets for data-scarce scenarios, and graph-centric methods use contrastive loss for self-supervised bootstrapping of robust graph representations [12]. Other techniques include Ski’s “assemble augmentation” for data-level bootstrapping to enrich training data [5], and AutoElicit’s use of Maximum Likelihood Estimation (MLE) and No-U-Turn Sampler (NUTS) to bootstrap an understanding of LLM behavior from its outputs for refining posterior knowledge [19]. A “mixed training” approach, combining raw data with task-specific QA, also serves as a form of bootstrapping by enabling efficient knowledge extraction from the outset [73]. Lastly, DKA employs input refinement (knowledge selection via BLIP model re-ranking) and output robustness (answer ensemble via maximum log-probability) as optimization strategies to enhance LLM performance in knowledge-based Visual Question Answering [61].
Limitations and Future Directions: A common limitation across many optimization and bootstrapping methods is the inherent computational cost, particularly for recursive or iterative processes and those requiring extensive evaluations (e.g., bi-level optimization in knowledge sharing, GRPO in LBMs, AutoPrompt’s greedy search) [8,43,50]. The “train from scratch” approach in active learning, while preventing overfitting, also incurs high computational costs and limits scalability [57]. Manual tuning of thresholds, scores, and hyperparameters (e.g., in EneRex and DKA) remains a challenge, suggesting a need for more principled, dynamic parameter determination [51,61].
Many bootstrapping mechanisms are highly domain-specific (e.g., robotics simulation, AlphaZero concept discovery, assembly code token pruning), and their generalizability across vastly different contexts is often not extensively analyzed [35,54,64]. The “reality gap” in robotics simulations and the assumption of “quasi-static knowledge state” in some systems limit applicability to dynamic, real-world scenarios [50,64]. Furthermore, while theoretical guarantees exist for some recursive bootstrapping methods (e.g., Optimal Transport), many practical implementations are heuristic, lacking robust convergence analyses or comparative studies against state-of-the-art alternatives [46,69]. The inability of current LLM-based KG construction to consistently outperform traditional small models for accuracy in specific tasks points to limitations in the effectiveness of current bootstrapping techniques for achieving domain-specific precision [12].
Future research should focus on developing more computationally efficient and theoretically robust recursive bootstrapping algorithms, particularly those that can dynamically adapt to evolving knowledge and leverage implicit knowledge representations in deep latent spaces without explicit labels. Investigating novel multi-objective optimization algorithms that balance correctness, completeness, and granularity in knowledge acquisition pipelines, especially in dynamic and uncertain environments, remains crucial [55]. Enhancing the interpretability of bootstrapped knowledge, particularly in prompt generation for LLMs, and bridging the gap between theoretical frameworks and large-scale practical implementations are also vital. Lastly, exploring methods for reducing the manual effort in defining reward functions and constraints, potentially through meta-learning or automated discovery, could significantly improve the scalability and applicability of these powerful KAB-attacking techniques.
5.3.3 Network Architecture and Parameter Transfer Techniques
Network Architecture and Parameter Transfer Techniques
| Technique Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Net2Net | Function-preserving architectural expansion (widening/deepening). | Accelerates training of larger networks, avoids retraining from scratch. | Net2WiderNet, Net2DeeperNet. | Limited to functional transfer, constrained by activation functions. |
| Transfer Learning (General) | Adapting pre-trained models to new tasks/domains. | Reduces data dependency, accelerates learning, leverages broad knowledge. | PLMs (BERT, T5, RoBERTa), ImageNet pre-training for CNNs. | OOD generalization, architectural mismatch, interpretability of transferred features. |
| Pluvio (CVIB) | Conditional Variational IB to learn domain-invariant representations. | Robust generalization to unseen architectures/compilers (binary analysis). | All-mpnet-base-v2 + CVIBEncoder. | Assumes sufficient “text-like” regularities, may lose subtle context. |
| PEFT (LoRA, Adapters) | Parameter-Efficient Fine-Tuning; small tunable modules. | Reduces computational cost of fine-tuning large models, mitigates catastrophic forgetting. | LoRA, Adapters, K-Adapter, DEMix-DAPT, Lifelong-MoE. | Can have limited expressiveness compared to full fine-tuning. |
| Knowledge Distillation | Transfers knowledge from a teacher model to a student model. | Replicates behavior efficiently in smaller models, enables collective learning. | Traditional KD (KL divergence), DWML (mutual learning among students). | Can lose nuance, increased complexity not always better, “dark knowledge” transfer. |
| KG Integration with LMs | Infusing structured KG knowledge into language models. | Enhances factual accuracy, reasoning, provides domain expertise. | Input/Intermediate/Objective layer injection, KGTransformer. | Semantic loss, interference between signals, “ineffective utilization,” limited for dynamic KGs. |
| Concept Transfer (Game AI) | Extracting and communicating abstract concepts from AI latent space. | Bridges human-AI knowledge gap, makes AI strategies interpretable. | AlphaZero (student network evaluation, concept amplification). | Limited to specific model types, linearity assumption for concepts. |
| Skill Transfer (RL) | Reusing learned behaviors or encoders across tasks/environments. | Accelerates learning in new environments, improves exploration. | InfoBot (learned encoders for decision states), IBOL (skill libraries). | Requires shared latent spaces or comparable dynamics, “reality gap” for robotics. |
Effective knowledge acquisition in deep learning relies heavily on sophisticated network architectures and strategic parameter transfer techniques. These methods aim to accelerate learning, reduce data dependency, and enhance model generalization by leveraging existing knowledge. This section delves into various approaches, from dynamic network manipulation to advanced transfer learning paradigms, critically assessing their mechanisms, strengths, weaknesses, and implications for diverse applications.
One direct method for dynamically adjusting network structure and transferring knowledge is the “Net2Net” technique, comprising Net2WiderNet and Net2DeeperNet [62]. Net2WiderNet expands a layer by increasing the number of units or convolutional channels. Knowledge transfer is achieved by copying existing weights for the input side of the widened layer and distributing weights for the output side, scaled by the replication factor. Specifically, for an input layer i and an output layer i+1, the weights are transferred as $\mathbf{U}^{(i)}{k,j} = \mathbf{W}^{(i)}{k, g(j)}$ for the input side and $\mathbf{U}^{(i+1)}_{j,h} = \frac{1}{ |
{x | g(x) = g(j)} | } \mathbf{W}^{(i+1)}_{g(j), h}$ for the output side, where $g$ is a random mapping function ensuring unit replication [62]. Similarly, Net2DeeperNet inserts new layers into an existing network. Parameter transfer involves initializing the new layer’s weights to perform an identity function, often by setting the weight matrix to an identity matrix for ReLU activations or using identity filters for convolutional networks. For batch normalization layers, output scale and bias are configured to nullify normalization effects, requiring an estimation of activation statistics through forward propagation [62]. These techniques enable a larger network to start from a state functionally equivalent to a smaller, fully trained network, thereby accelerating the learning process by bypassing retraining from scratch. A key assumption for Net2DeeperNet is the activation function’s capacity to support identity mappings (e.g., ReLU is suitable, logistic sigmoid is not) [62]. While powerful for architectural growth, these methods primarily address scaling within a network type and do not inherently tackle challenges like cross-modal or symbolic knowledge transfer. |
A more generalized approach to knowledge acquisition involves transfer learning and information bottleneck principles, particularly exemplified by Pluvio [24]. Traditional transfer learning, widely observed in the fine-tuning of pre-trained language models (PLMs) such as BERT, T5, and RoBERTa, leverages extensive linguistic and world knowledge acquired from massive text corpora [6,38,52]. This general knowledge is then transferred and adapted (fine-tuned) to specific downstream tasks, significantly reducing the need for extensive task-specific data and accelerating convergence [1,41,51,63].
Pluvio extends this paradigm by integrating a Conditional Variational Information Bottleneck (CVIB) into its architecture, specifically using all-mpnet-base-v2 as its core [24]. Unlike standard fine-tuning, Pluvio’s CVIB explicitly addresses the “out-of-domain” knowledge acquisition bottleneck by forcing invariance to nuisance factors. It conditions on “nuisance labels” (e.g., architecture and optimization settings, $l_a$, $l_o$) during training, aiming to “forget” information related to these variables. This ensures that the learned latent representations ($Z$) disentangle domain-specific variations from the core semantic or functional aspects of the assembly code. The practical objective function for CVIB, which incorporates the reparameterization trick, involves an expectation over noise and a KL divergence term. The reparameterization trick is formulated as $f(e)=\mu_z(e) + \sigma_z(e) \cdot \epsilon_z$, where $\mu_z$ and $\sigma_z$ are the mean and standard deviation of the distribution, and $\epsilon_z$ is a sample from a noise distribution [24]. This mechanism yields robust, domain-invariant embeddings, which is a unique advantage over traditional fine-tuning that might struggle with significant domain shifts without explicit disentanglement. However, Pluvio’s efficacy relies on the assumption that assembly code possesses sufficient “text-like” semantic regularities transferable from natural language, a premise that may not universally hold, especially for highly obfuscated code.
The application of pre-training and fine-tuning extends across various domains and architectural types. In robotics, ImageNet pre-training for Convolutional Neural Networks (CNNs) is a prominent example of parameter transfer, where networks learn rich visual features from vast image datasets and transfer them to visual tasks like servoing and grasping, significantly reducing robot-specific data needs [29,64]. This leverages the strength of large-scale supervised learning in a source domain (ImageNet) to a data-scarce target domain (robotics). For game AI, the student-teacher paradigm facilitates concept transfer. AlphaZero’s latent space can represent learned concepts, and a “student network” (an AlphaZero checkpoint) is used to evaluate the teachability of these concepts, representing an implicit parameter transfer where a less knowledgeable model is “taught” [54]. Concept amplification, achieved by perturbing the network’s latent representation, further validates the causal influence of these concepts on the model’s behavior [54]. Similarly, InfoBot uses learned encoders for exploration strategies, transferring knowledge about salient states rather than direct policy parameters across different Atari games, accelerating learning in new environments [56].
Parameter-Efficient Fine-Tuning (PEFT) methods, such as Low-Rank Adaptation (LoRA) and Adapters, have emerged to address the high computational costs of fine-tuning large models. LoRA, for instance, decomposes weight updates into low-rank components, allowing the base LLM parameters to remain frozen while adapting to new knowledge by updating only smaller matrices. This approach efficiently transfers pre-trained knowledge to specific tasks without modifying the entire model [2,4,13,66,73]. Other PEFT techniques like K-Adapter and modular experts (e.g., DEMix-DAPT, Lifelong-MoE) also enable efficient knowledge transfer by adding lightweight, task-specific modules or freezing previously trained parameters, mitigating catastrophic forgetting in continual learning [20].
The integration of knowledge graphs (KGs) into language models presents another facet of architectural and parameter transfer. Strategies include input-layer injection (converting KGs to natural language), intermediate-layer injection (integrating pre-trained KG embeddings with attention mechanisms), and objective-layer injection (multi-task learning with combined loss functions) [7,12,74]. These methods aim to infuse structured knowledge into PLMs, often leveraging specialized Transformer models designed for graph structures like KGTransformer [12]. However, some injection methods can lead to semantic loss or interference between textual and structural signals, potentially degrading the quality of transferred parameters [12]. Critically, architectural innovations in some knowledge injection frameworks have been shown to suffer from ineffective knowledge utilization or knowledge complexity mismatch, failing to distinguish aligned knowledge from random inputs during fine-tuning [7].
Knowledge distillation is a parameter transfer technique where knowledge is transferred from a larger “teacher” model to a smaller “student” model. This can involve aligning class posteriors through KL divergence loss. A notable extension is Diversity Induced Weighted Mutual Learning (DWML), where knowledge is implicitly transferred between diverse peer student models without a single teacher, dynamically weighting contributions from more capable peers [8]. This approach highlights the potential for collective knowledge transfer among heterogeneous architectures.
The implication of architectural mismatch on model extraction efficiency has been explored in the context of functional knowledge transfer. Studies demonstrate that functional knowledge can be transferred from a secret Deep Neural Network (DNN) to a substitute DNN even when their architectures are not identical. For instance, high agreement scores (e.g., 97.21% on MNIST for a less complex substitute) can be achieved despite architectural differences, although matching architectures generally lead to optimal transfer [15]. This suggests that functional knowledge is transferable across models of varying complexities, with performance degradation attributed to underfitting or overfitting in the substitute model [15]. However, this transfer is often behavioral emulation rather than direct parameter sharing. Conversely, despite parameter transfer via pre-training, models often exhibit significant performance degradation when applied zero-shot to highly specialized, out-of-domain applications (e.g., aviation maintenance), indicating limitations of current techniques in bridging large domain gaps without specific fine-tuning [48]. This highlights a crucial challenge in balancing generalizability with domain specificity. Furthermore, certain pre-training strategies might surprisingly degrade final model quality for specific tasks, even while accelerating convergence, suggesting a nuanced interaction between general-purpose knowledge and task-specific fine-tuning, potentially indicative of an architectural mismatch or knowledge transfer barrier [49].
Observations about model properties, such as scaling behavior, reveal important aspects of knowledge utilization. While the scaling of pre-trained language models does not represent a technique itself, findings suggest that larger models can achieve higher levels of factual transfer and generalization, implying that network architecture and scale play a crucial role in efficient knowledge acquisition [60]. However, this scaling often comes with high training costs and scalability challenges [12]. The effectiveness of these large models in structured knowledge tasks is not always superior to traditional smaller models, indicating limitations in current parameter transfer and network adaptation techniques for highly specialized problems [12].
Despite the advancements, several limitations and areas for improvement persist. Many studies rely on existing powerful PLMs and standard deep learning architectures without introducing novel Net2Net techniques for dynamic network manipulation or specific CVIB formulations for robust, disentangled embeddings [3,7,38,42]. The computational cost and resource demands of large LLMs also present a significant computational cost concern for their widespread application [50]. Future research should focus on developing more generalized Net2Net methods beyond specific activation functions, exploring explicit CVIB for diverse domains and nuisance factors, and investigating architectural strategies that intrinsically support knowledge disentanglement and effective utilization, especially in hybrid neurosymbolic systems [58]. Addressing how to fundamentally overhaul training data, optimization functions, and architectural constraints will be key to better cognitive alignment and overcoming the inherent knowledge acquisition bottleneck [12].
5.3.4 Forgetting and Consolidation Algorithms (Incremental Learning)
The efficient management of acquired knowledge, particularly through mechanisms of forgetting and consolidation, is paramount for systems aiming to overcome the Knowledge Acquisition Bottleneck (KAB) and achieve true incremental and cumulative learning [67]. This domain directly addresses the Stability-Plasticity dilemma, where systems must balance the assimilation of new information (plasticity) with the retention of previously learned knowledge (stability) [67].
Frameworks and Algorithms for Knowledge Management
Forgetting and Consolidation Algorithms for Incremental Learning
| Strategy / Algorithm | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Knowledge Management (MML-based) | Rule selection based on informativeness (Hierarchical Support, Optimality). | Prevents information overload, ensures manageable/relevant knowledge base. | Forgetting (removes low-info rules), Consolidation (promotes robust rules), Demotion. | Explicit criteria definition, complex for non-rule-based systems. |
| Agent KB (Dynamic Experience Mgmt.) | Merges similar experiences, prunes outdated/low-value experiences. | Maintains relevant experience base, avoids suboptimal knowledge. | Adaptive experience valuation, epistemic weights. | Defining “similarity” and “value,” potential for bias in valuation. |
| KnowMap (Factual Updates) | Replacement mechanism for environmental facts. | Maintains current factual knowledge, externalizes LLM adaptation. | Replacement mechanism, externally fine-tuned embedding model. | Limited scope to instance-level facts, scalability for large data if not managed. |
| SAC-KG (KG Refinement) | Generator-Verifier-Pruner framework. | Selective consolidation, prevents incorrect/irrelevant knowledge. | Verifier (error detection), Pruner (growth guidance). | Relies on rule criteria, hallucination risks for LLM generators. |
| R1-Searcher++ (Internalization) | LLM internalizes retrieved external knowledge into memory. | Persistent knowledge, reduces repeated external queries. | External Knowledge Memorization (two-stage RL training). | Effectiveness of internalization, potential for knowledge conflicts. |
| MVKM (Dynamic Knowledge Modeling) | Rank-based constraint on knowledge growth, allows for forgetting. | Realistically models learning/forgetting, tracks dynamic knowledge. | Multi-view tensor factorization, flexible knowledge increase objective. | Assumes rank-based mechanism, requires diverse learning materials. |
| Mitigating Catastrophic Forgetting (LLMs) | Strategies to preserve previously acquired knowledge during updates. | Balances stability & plasticity, enables continual learning. | Can introduce side effects, often requires architectural changes. | |
| Data Replay | Periodically reintroduces original training samples. | Reactivates latent circuit components, maintains knowledge elasticity. | Periodical reintroduction of fixed ratio of samples. | Computationally intensive, storage of old data. |
| Regularization-Based | Penalizes changes in critical parameters. | Preserves essential information, prevents overwriting. | RecAdam, DSA. | Requires identification of “critical” parameters, potential for over-regularization. |
| Architectural-Based | Freezes original parameters, uses lightweight adapters. | New knowledge through modular additions, maintains integrity. | K-Adapter, LoRA, DEMix-DAPT, Lifelong-MoE. | Can add model complexity, potential for architectural mismatch. |
| Knowledge Editing | Targeted updates to LLM parameters. | Preserves previous edits, avoids unintended side effects. | GRACE (caches layer activations). | Side effects, limited propagation of edited knowledge. |
| Knowledge Entropy Resuscitation | Increases activity of inactive memory vectors. | Increases plasticity, reduces forgetting. | Heuristic parameter scaling (Algorithm 1). | Heuristic approach, generalizability across different LLM architectures. |
| Implicit Forgetting for Generalization | Forgetting nuisance information during learning. | Enhances OOD generalization, disentangles semantics. | Pluvio (Conditional VIB), IBOL (disentangled skills). | Requires identifiable nuisance factors, potential for losing subtle context. |
Key to incremental learning are frameworks that explicitly define strategies for knowledge retention, modification, and discarding. The theoretical foundation often draws from cognitive science, recognizing that human learning involves continuous integration and coherence management of knowledge [46,72].
One such principled framework introduces explicit algorithmic procedures for forgetting and consolidation, governed by MML-derived metrics such as Hierarchical Support ($\mathcal{S}_C$), Optimality (measureC), Permanence (perm), and Residual (resc) [67]. These metrics quantify the utility and informativeness of rules, enabling a decision-making process for knowledge management.
- Forgetting Algorithm: Designed to prevent information overload by removing “useless” or irrelevant rules, typically those with low informativeness (e.g., low $\mathcal{S}_C$), from a temporary working space (short-term memory). This process is selective, abstracting concepts by discarding differences, rather than a catastrophic loss [67].
- Consolidation (Promotion) Algorithm: Rules deemed highly reliable and robust based on MML metrics are “promoted” from the working space to a consolidated knowledge base (long-term memory). This strengthens their role as foundational knowledge for future learning [67].
- Demotion System: To prevent the long-term knowledge base from becoming unmanageably large or inconsistent, rules can be “demoted” back to the working space or entirely forgotten if their utility or consistency degrades over time [67].
Other systems also incorporate explicit or implicit mechanisms for managing knowledge evolution:
Agent KBemploys both consolidation and forgetting, merging similar experiences across agents and pruning outdated or low-value experiences based on an adaptive experience valuation mechanism. This mechanism iteratively adjusts epistemic weights based on task-solving efficacy, ensuring the removal of suboptimal knowledge [33].- KnowMap utilizes an
environmental knowledge basewith a replacement mechanism for factual updates, superseding old information with new to maintain currency. To mitigate catastrophic forgetting in the core Large Language Model (LLM), it avoids full fine-tuning, relying instead on a small, externally fine-tuned embedding model for dynamic knowledge adaptation. This architectural choice externalizes adaptation, preserving the LLM’s general capabilities. Itsexperiential knowledge basecumulatively incorporates task trajectories, promoting lifelong learning through accumulation without explicit forgetting algorithms, which could lead to scalability issues if not managed [44]. - SAC-KG iteratively generates and refines Knowledge Graphs (KGs). Its
VerifierandPrunermodules ensure that only high-quality, relevant knowledge is integrated, effectively “forgetting” or preventing the inclusion of incorrect or irrelevant information by filtering entities and discarding potential growth paths [66]. This acts as a selective consolidation process, focusing on maintaining coherence within specialized domain KGs. - R1-Searcher++ addresses knowledge consolidation by explicitly training the LLM to internalize retrieved external knowledge, transforming it into persistent internal memory. This mechanism, termed “External Knowledge Memorization,” enables continuous assimilation and efficient reuse of acquired knowledge, enriching the LLM’s internal state and evolving towards greater intelligence [27]. This contrasts with prior RL-based RAG models that over-relied on external search, indicating a deficiency in internal knowledge retention.
- MVKM (Multimodal Visual Knowledge Model) explicitly models forgetting through a rank-based constraint on student knowledge growth, allowing for occasional loss. It penalizes scenarios where current knowledge is less than previous knowledge, and for synthetic data, forgetting is simulated as a random decrease in knowledge if a
forgetting thresholdis met [22].
Mitigating Forgetting and Enabling Consolidation in LLMs
For Large Language Models, catastrophic forgetting remains a significant challenge during continual learning, where new information can overwrite previously acquired knowledge [5,12,20,30].
- Data Replay Interventions and Knowledge Circuit Elasticity: Research indicates that LLMs possess “knowledge circuit elasticity,” demonstrating a capacity for structural reconfiguration.
Data replay interventions, which involve periodically reintroducing a fixed ratio of original training samples, successfully reactivate latent circuit components and mitigate knowledge loss during subsequent continual pre-training [34]. - Regularization-based Methods: Algorithms like
RecAdamandDSAapply penalties to changes in critical parameters associated with previous knowledge, acting as a consolidation mechanism to preserve essential information during updates [20]. - Architectural-based Methods: Approaches such as
K-Adapter,LoRA, andCPTprevent forgetting by freezing original LLM parameters and introducing lightweight, tunable adapters for new tasks. Modular expert architectures likeDEMix-DAPTandLifelong-MoEprogressively expand, freezing previously trained experts to maintain existing knowledge integrity [20]. - Continual Knowledge Editing:
GRACEmitigates forgetting of previous edits by caching layer activations and retrieving them when similar edits are needed, ensuring edit persistence without unintended side effects [20]. - Self-Tuning: The
Self-Tuningframework incorporates a “reviewing mechanism” that periodically assesses the model’s existing skills while acquiring new knowledge, implicitly consolidating prior learning and demonstrating robustness against catastrophic forgetting. It also suggests future integration with continual learning approaches like regularization-based and replay-based methods for enhanced retention [68]. - Knowledge Entropy Decay: The observation that decreasing
knowledge entropyin LLMs (reliance on a narrower set of memory vectors) contributes to increased forgetting. The proposed “resuscitation” algorithm aims to counteract this by increasing the activity of previously inactive memory vectors, implicitly creating more space for new knowledge and reducing overwriting [69]. - Contrast with Static Fine-tuning: In some fine-tuning strategies, a low learning rate is intentionally applied, and weight decay is omitted “to prevent any forgetting” [53]. This approach prioritizes stability by minimizing parametric changes, reflecting a quasi-static knowledge assumption during the fine-tuning phase rather than active management of dynamic knowledge.
Trade-offs in Forgetting: Selective Discarding vs. Information Loss
The decision to forget involves critical trade-offs. Forgetting can prevent negative transfer or information overflow, but it risks losing valuable information.
- Explicit Discarding for Coherence and Efficiency: Frameworks like the one based on MML metrics [67] and
Agent KB[33] explicitly prune low-utility or outdated knowledge, ensuring a manageable and relevant knowledge base. Similarly,Concept Unlearningallows for targeted removal of specific concepts, such as biased terms, by deactivating neurons or removing weights in Concept Bottleneck Layers, improving fairness and interpretability [32]. This is a deliberate “forgetting” to achieve a specific systemic goal. - Implicit Forgetting for Generalization: In contrast to explicit forgetting of acquired knowledge,
Pluvioleverages a Conditional Variational Information Bottleneck (CVIB) as an inherent “forgetting” mechanism during training [24]. CVIB conditions on “nuisance labels” (e.g., architecture or optimization details) to penalize their retention in the latent representation. This forces the model to learn invariant embeddings that disentangle the functional semantics of assembly code from domain-specific features. The “forgetting” here is not about discarding outdated learned knowledge but about filtering out context-dependent, potentially distracting features to enhanceout-of-domain (OOD) generalization[24,64].
Implications of the “Quasi-Static Knowledge State” Assumption Many current models, by design or limitation, operate under an assumption of a “quasi-static knowledge state,” where the knowledge base is considered fixed during operation or only updated in a piecemeal fashion without explicit dynamic management.
- Examples: Language Bottleneck Models (LBMs), in their current form, assume a student’s knowledge state is fixed during a diagnostic session, deferring dynamic evolution to future work [50]. Fine-tuning LLMs with low learning rates to prevent forgetting implicitly assumes the parametric knowledge is static and should be preserved [53]. Similarly, retraining models “from scratch” in active learning rounds, though preventing catastrophic forgetting, implicitly treats each learning phase as independent rather than incrementally building on prior knowledge [15,45,57]. Initial KG construction efforts also often operate on a static corpus, extracting knowledge as a snapshot in time [11,31,40,74]. Latplan’s generated PDDL models also represent a “quasi-static knowledge state” of an environment [28]. The phenomenon of LLMs forgetting how to reproduce source text during finetuning on QA tasks also points to a quasi-static assumption for the finetuning task itself [73]. The
Ineffective Knowledge Utilizationobserved in LLMs, where injected knowledge acts as noise, suggests models lack internal mechanisms for dynamic knowledge management and implicitly treat new knowledge as a static addition rather than requiring integration and consolidation [7]. - Limitations: This assumption significantly limits long-term applicability and adaptability, particularly in dynamic environments where knowledge continuously evolves. Systems designed for static knowledge states struggle with issues like
scalability,dynamic knowledge maintenance, andarchitectural mismatchwhen faced with real-world changes [3,17,39,50]. - Recognizing Dynamic Knowledge: Some systems, like NELL and DBpedia, implicitly acknowledge dynamic knowledge. NELL continuously extracts and refines knowledge, removing incorrect facts and integrating new information [55]. DBpedia’s
Sievemodule prioritizes timely and reliable information, implicitly consolidating current facts over older ones [55]. This highlights the necessity for explicitknowledge evolution managementas a future challenge [52,55].
Connecting to Lifelong Learning and Robotics
The concepts of forgetting and consolidation are critically important for lifelong learning systems, especially in robotics. Physical robot systems operate in dynamic, open-world environments where knowledge is not static and changes frequently [29,64].
- Adaptation to Dynamic Changes: Robots must adapt to
changing properties over timedue to wear, environmental factors (e.g., temperature), or even hardware defects. This necessitates mechanisms for continuous adaptation, where the robot implicitly “forgets” outdated understandings of its body dynamics and “consolidates” new behaviors to account for damage, ensuring continued functionality [64]. This is a form of knowledge update and consolidation for self-preservation and task completion. - Efficient Knowledge Retention and Utilization: Lifelong machine learning systems for robotics are defined by their ability to “efficiently and effectively retain the knowledge they have learned and use that knowledge to more efficiently and effectively learn new tasks” [64]. This requires sophisticated algorithmic procedures for managing acquired knowledge, deciding what to keep, and integrating new information while avoiding catastrophic forgetting. The ability to manage information overflow and redundancy through selective forgetting, as explored in rule-based systems, is vital for long-term operational efficiency in robots [67].
Limitations and Future Research Despite progress, significant challenges remain in developing robust forgetting and consolidation strategies for continuous learning systems.
- Lack of Algorithmic Specificity: Many papers highlight the need for dynamic knowledge management but lack detailed algorithmic procedures and explicit criteria for retention, modification, or discarding of knowledge components [3,7,12,30,37,58]. The
complexity of neural networksmakes it difficult to guarantee complete knowledge preservation and avoidside effectsorknowledge conflictsduring incremental updates [12,20]. - Scalability and Computational Cost: Approaches that rely on retraining on cumulative datasets become computationally expensive and inefficient for large-scale, lifelong learning scenarios [57].
- Dynamic Knowledge Evolution in KGs: While KG update strategies like incremental entity resolution, data cleaning, and version control provide some mechanisms for adapting to changes, the challenge of fully autonomous, complex ontology refactoring (e.g., merging duplicate concepts or removing entire sub-hierarchies) remains significant [3,17,71].
- Bridging Cognitive and AI Models: Translating principles of “recursive consolidation” observed in biological systems into concrete AI algorithms for preventing catastrophic forgetting and ensuring knowledge coherence is an open research question [46,72]. Future research could explore using
knowledge entropyas a dynamic signal to trigger specific consolidation phases or guide selective forgetting in incremental learning systems [69]. - Effective Knowledge Utilization: The observed
Ineffective Knowledge Utilizationin LLMs, where injected knowledge is not meaningfully integrated, indicates a fundamental lack of robust internal mechanisms for knowledge management. Future work needs to focus on architectural modifications and algorithmic procedures that enable LLMs to discern and consolidate relevant information while forgetting noise [7].
Ultimately, the development of robust, theoretically grounded, and computationally efficient forgetting and consolidation algorithms is crucial for advancing AI systems towards truly adaptive, lifelong learning capabilities that can effectively manage dynamic knowledge, particularly in complex domains like physical robotics and ever-evolving information landscapes.
5.4 Knowledge Validation and Uncertainty Management
The efficient acquisition of knowledge is intrinsically linked to robust validation mechanisms and effective uncertainty management. These processes are critical for ensuring the reliability and utility of acquired knowledge, thereby mitigating the Knowledge Acquisition Bottleneck (KAB).
Knowledge Validation and Uncertainty Management Approaches
| Domain / Approach | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Knowledge Graphs (KGs) | Ensuring accuracy, consistency, timeliness, and trustworthiness. | Builds reliable, verifiable sources of truth. | Lack of end-to-end benchmarks, scalability of HIL, noisy facts. | |
| KG Validation | Rule-based checks, semantic reasoning, LLM-driven verification. | Automates quality control, mitigates hallucination. | MatSKRAFT (physicochemical constraints), Bench4KE (semantic similarity), KGValidator (LLM-based), Evo-DKD (consistency checks). | Manual effort for rule generation, LLM hallucination, sourcing context. |
| Uncertainty Management | Classifying, representing, and fusing uncertain knowledge. | Improves reliability, enables informed knowledge selection. | Knowledge deltas (Invalidity, Vagueness), Confidence scores (UKGE), Truth inferring (TruthFinder). | Complex data models, handling granularity differences, source reliability assessment. |
| Pre-trained Language Models (PLMs) | Assessing effective utilization of acquired knowledge. | Diagnoses utilization gaps, improves factual correctness. | Lack of direct insight into internal mechanisms, LLM-as-judge bias. | |
| Implicit Validation | Task performance as proxy for knowledge quality. | Measures usability in downstream tasks (e.g., document retrieval). | KAU framework, F1 score, nDCG@k, Recall@k. | Does not explain why failures occur, limited to observable performance. |
| Uncertainty Estimation | Quantifies model’s confidence or belief spread. | Guides active learning, identifies areas of low confidence. | Knowledge Entropy (FFNs), AutoElicit (Bayesian inference for priors). | May not reflect true understanding, needs human-interpretable output. |
| Robotics | Robustness & adaptability in dynamic, uncertain physical environments. | Ensures safety, reliability, and task completion. | Probabilistic methods (state estimation, collision probabilities). | Sim-to-real gap, black-box nature of learned behaviors, safety-criticality. |
| Game AI | Validating abstract, machine-unique concepts (M-H knowledge). | Bridges human-AI knowledge gap, expands human understanding. | Teachability (student AI), Novelty (spectral analysis), Human Validation (grandmasters). | Small sample size, relies on human experts, optimal “teachability” conditions. |
This section provides a comprehensive analysis of various approaches to knowledge validation and uncertainty management across different AI domains, highlighting underlying assumptions, theoretical foundations, architectural choices, and domain-specific adaptations.
Frameworks for Automatic Validation of Knowledge Graph Construction
The automatic validation of Knowledge Graphs (KGs), especially those constructed using advanced generative models, has emerged as a crucial area to maintain data quality and trustworthiness. Traditional KG validation focuses on ensuring accuracy, consistency, timeliness, completeness, and trustworthiness across multiple dimensions [3,55]. Methods include crowdsourcing and expert knowledge, statistical analysis, semantic reasoning (e.g., using OWL description logics or SHACL rules), and comparisons with external knowledge bases [3,36]. Rule-based analysis, employing manually generated constraints, is prevalent in systems like DBpedia and YAGO for automatic consistency checks [3]. The MatSKRAFT framework, for instance, employs multi-layered validation including physicochemical constraint checking (e.g., rejecting negative densities) and unit analysis to ensure scientific reliability in materials knowledge extraction [65]. Similarly, Bench4KE validates automatically generated Competency Questions (CQs) by comparing them against a gold standard dataset using various semantic similarity metrics, including LLM-based scoring, to ensure alignment with expert knowledge [14].
With the rise of generative models, particularly Large Language Models (LLMs), new validation paradigms have been proposed. The KGValidator framework explicitly leverages LLMs to automatically validate the correctness and consistency of Knowledge Graph Completion (KGC) model outputs, specifically ($h, r, t$) triples [40]. This system determines triple_is_valid based on factual validity, relevance, and semantic nuances, and critically, allows the LLM to respond with "Not enough information to say", thereby explicitly flagging uncertainty. This mechanism directly contributes to reducing the KAB by improving the reliability of ingested triples. Another LLM-driven approach, SAC-KG, uses a Verifier component that identifies error types (e.g., “Quantity insufficient,” “Contradiction”) based on rule criteria and performs error correction through reprompting the LLM, alongside a Pruner for quality control that ensures only relevant entities contribute to KG expansion [66]. Evo-DKD further refines this by incorporating a Validation Module that checks for ontology consistency (e.g., schema constraint violations, redundancy) and cross-checks the natural language justification provided by the LLM against the structured claim, rejecting or flagging edits that fail these checks [17]. Such methods are crucial given that LLMs can generate KGs with correctness rates as low as 20% for long-tail domains, necessitating robust validation to counteract hallucination problems [12].
Beyond direct KG construction, the validation of extracted knowledge from unstructured text for KGs or other representations is frequently achieved through rigorous evaluation against ground truth datasets using metrics like F1, precision, and recall [48,51]. AXCELL validates extracted scientific results by filtering records based on model association and selecting the best results for leaderboards, assigning linking scores and applying confidence thresholds based on Bayesian inference to manage quality [41]. StructSense employs a judge agent that assigns confidence scores to extracted information and aligns it with ontological concepts, augmented by human-in-the-loop (HIL) feedback for mitigating hallucinations and refining outputs [70].
Uncertainty Management in Knowledge Graph Construction
The critical issue of “uncertainty management in the construction of knowledge graphs” is addressed by classifying knowledge uncertainty into “knowledge deltas” such as Invalidity, Vagueness, Fuzziness, Timeliness, Ambiguity, and Incompleteness, which manifest as Granularity or Contradictory conflicts [55]. Effective strategies involve preserving and representing uncertainty (e.g., confidence scores, provenance) within the KG as metadata, allowing for knowledge selection based on confidence during querying [55]. Various data models like Singleton Property, Property Graph, and RDF-star are discussed for their ability to annotate edges and reference edges, supporting uncertainty representation [55]. Uncertain Knowledge Graph Embedding (UKGE) models explicitly integrate confidence scores into their learning, with evaluation tasks like confidence prediction and relation fact ranking directly quantifying uncertainty in the embedding space [55]. Knowledge fusion methods (e.g., TruthFinder, ACCU) further manage uncertainty by estimating source trustworthiness and inferring true values from conflicting claims, thereby aiming for correctness and completeness [55].
Strategies for handling “additional uncertainty” introduced during knowledge extraction significantly impact the reliability and utility of KGs for “downstream tasks after knowledge acquisition” [55]. KRDL resolves noisy and contradictory information from weak supervision sources by modeling prior knowledge using weighted first-order logical formulas, where formula weights represent confidence and are refined during learning [16]. The joint inference component imposes soft and hard constraints to validate consistency. For LLMs, gpt_3_powered_information_extraction_for_building_robust_knowledge_bases uses logit bias and contextual calibration to manage prediction uncertainty and biases, while knowmap_efficient_knowledge_driven_task_adaptation_for_llms employs a replacement mechanism for environmental facts to ensure consistency and currency, implicitly prioritizing more recent and relevant information. The revisiting_the_knowledge_injection_frameworks approach purifies and prunes conceptual knowledge to manage the knowledge complexity mismatch arising from vast and intricate KGs, implicitly reducing uncertainty by presenting cleaner, more concise knowledge. DKA in visual QA re-ranks retrieved external knowledge based on image-knowledge correlation, selecting only top-$n$ items to reduce retrieval noise and filter out less relevant or uncertain information [61].
Implicit Validation of Knowledge Usability in PLMs
While not a general KG validation framework, measuring_the_knowledge_acquisition_utilization_gap_in_pretrained_language_models provides an implicit validation of knowledge usability in Pretrained Language Models (PLMs). It assesses the utility of acquired knowledge by measuring its application in downstream tasks, where correct retrieval in document matching serves as an indicator of validated, usable knowledge. This approach assumes that successful task performance is a proxy for the quality and usability of the model’s internal knowledge. Similarly, other LLM-focused works validate knowledge by evaluating performance on QA tasks, often using metrics like F1 score, nDCG@k, and Recall@k to assess factual correctness and utility [5,73]. The R1-Searcher++ framework, for instance, uses F1-score and LLM-as-Judge to validate the factual accuracy of final answers, while its adaptive decision-making to invoke external search when “confused” or lacking information represents an implicit uncertainty management strategy [27]. AutoElicit leverages Bayesian inference with LLM-elicited priors to provide accurate estimates of predictive uncertainty and uses metrics like Energy Statistic and Bayes Factor to validate the consistency and reliability of LLM-derived knowledge [19]. However, the observation that LLMs’ performance significantly drops on “perturbed sentences” with incorrect facts highlights a limitation in their uncertainty management for distinguishing known facts from contextually extracted information, suggesting a need for better robustness to inconsistencies [43]. Furthermore, the concept of Knowledge Entropy is used to quantify the internal uncertainty or variability in how LLMs utilize parametric knowledge, where decreasing entropy during pretraining correlates with increased certainty but can paradoxically hinder new knowledge acquisition, presenting a complex trade-off [69].
Cross-Domain Comparison: KGs, Robotics, and Game AI The approaches to knowledge validation and uncertainty management diverge significantly across KGs, robotics, and game AI due to their distinct objectives, operational environments, and forms of knowledge.
Knowledge Graphs (KGs) primarily focus on explicit, symbolic representations of facts and relations. Validation emphasizes consistency, accuracy, and logical integrity against predefined schema and real-world knowledge [3,55]. Uncertainty in KGs is formally represented through confidence scores, probabilistic facts, or truth discovery methods that evaluate source reliability [3,55]. Mechanisms often involve structured checking (e.g., OWL reasoners [36]), rule-based verification, and human-in-the-loop curation for explicit error detection and correction [59]. The goal is to build KGs as reliable, verifiable sources of truth, crucial for applications requiring high precision and explainability.
Robotics, conversely, deals with perception and action in dynamic, uncertain physical environments, where “information about the world is usually incomplete and knowledge is not certain” [64]. The core of validation and uncertainty management lies in the robustness and adaptability of learned behaviors in the face of sensorimotor uncertainty and noise [64]. Probabilistic methods are widely adopted to handle uncertainty in state estimation and control. For instance, learned policies can compensate for imperfect state estimation in pick-and-place tasks, or uncertainty-aware collision avoidance models predict collision probabilities from camera images to enable cautious navigation or faster movement when confidence is high [64]. Validation is implicit, often measured by successful task completion, safety, and resilience under varying conditions. The assumption is that successful action in an uncertain world implies valid, robust internal models, even if these models “ignore or forget information” to achieve robustness [64].
Game AI presents a unique validation challenge, particularly for AI-discovered concepts that may not align with human intuition. bridging_the_human_ai_knowledge_gap_concept_discovery_and_transfer_in_alphazero introduces a multi-faceted validation approach for AlphaZero-discovered concepts, moving beyond traditional accuracy metrics. Key validation criteria include:
- Teachability: This metric assesses the utility and transferability of a concept by training a student network (an AlphaZero checkpoint) on concept-specific prototypes and evaluating its performance. Concepts are only deemed valid if the student’s performance significantly improves in terms of top-1 move overlap with the teacher, effectively filtering out 97.6% of initial concepts [54].
- Novelty: To confirm that concepts represent machine-unique knowledge ($M-H$), a novelty score is calculated using spectral analysis. This quantifies how much better a concept vector is explained by AlphaZero’s internal “language” compared to human game data, filtering an additional 27.1% of concepts that are too human-like [54].
- Human Validation: Ultimately, human studies with chess grandmasters validate the real-world utility and comprehensibility of these AI-discovered concepts, as evidenced by improved performance on concept-based puzzles [54].
Unlike KGs which demand explicit consistency or robotics which prioritizes robust action, game AI validation focuses on the quality and uniqueness of abstract concepts, implicitly assuming that if a concept is teachable and novel, it contributes valuable, non-trivial knowledge. Uncertainty management in this domain is more about rigorous filtering and quality control of discovered concepts rather than probabilistic representation within the concepts themselves.
Limitations and Future Research
Despite significant advancements, several limitations and areas for improvement remain. For KGs, evaluating quality remains challenging due to the lack of widely used end-to-end benchmark datasets, making it difficult to define robust validation criteria that are context and use-case dependent [3]. The scalability of human-in-the-loop validation, while effective, is a practical bottleneck. There is a need for a unified, robust framework for dynamic, continuous knowledge validation in KGs that can simultaneously handle evolving uncertainties, mixed data types, and varying granularities [55]. Specifically, the “Consistency Checking” module in proposed ideal pipelines needs to transition from reactive to proactive and intelligent to preemptively address potential inconsistencies [55]. For LLM-generated KGs, the inherent error rates, especially in long-tail domains, necessitate the development of more intrinsic self-validation mechanisms within LLMs, rather than solely relying on external KG references for validation [12].
In the context of learned behaviors in robotics, the observation of emergent properties, both positive and negative (e.g., “reward hacking”), highlights that validation of learned knowledge still presents challenges, requiring further research into ensuring desired behaviors and preventing unintended consequences [64]. For game AI, quantifying uncertainty in discovered concept vectors or their application, and assigning confidence scores to guide human learning or further AI refinement, represents a critical unaddressed question [54]. More broadly, understanding the trade-off between increased certainty (low knowledge entropy) and the impaired ability to acquire new knowledge in LLMs is crucial for designing more adaptable and continuously learning AI systems [69]. Addressing knowledge conflicts within LLM outputs and developing principled mechanisms for prioritizing conflicting information sources are also open challenges [20]. Overall, future research needs to focus on developing more rigorous, scalable, and domain-agnostic frameworks that integrate validation and uncertainty management intrinsically throughout the knowledge acquisition lifecycle.
6. Applications and Case Studies
The effective mitigation of the knowledge acquisition bottleneck (KAB) is pivotal for extending the capabilities of Artificial Intelligence across a myriad of real-world scenarios. This section provides a comprehensive overview of how various frameworks and algorithms, designed to overcome the KAB, are applied, adapted, and validated across diverse domains, transforming theoretical advancements into practical solutions. These applications collectively demonstrate the critical role of systematic knowledge acquisition in enhancing AI capabilities, improving efficiency, reducing manual effort, and enabling novel functionalities previously unattainable.
At the core of these applications lies a unifying theoretical framework that acknowledges the limitations of implicitly stored, parametric knowledge within many AI models, particularly Large Language Models (LLMs). This framework posits that for AI systems to achieve consistent reliability, factual accuracy, and interpretability, there is an imperative to externalize and structure knowledge, often in the form of Knowledge Graphs (KGs) and ontologies [12,30]. This structured knowledge provides verifiable, dynamic, and semantically rich context, moving systems beyond purely data-driven paradigms towards more robust, knowledge-driven intelligence. Key overarching principles guiding these applications include the pursuit of enhanced interpretability and explainability for transparent decision-making, particularly in sensitive domains [39,50]; the development of adaptable and generalizable systems capable of operating in dynamic and “out-of-domain” contexts, often through transfer learning and the discovery of invariant representations [24,47]; and the focus on efficiency and automation to reduce labor-intensive manual annotation and data processing bottlenecks [19,57].
In Natural Language Processing (NLP) and Generative AI, knowledge acquisition directly addresses challenges such as factual inconsistency and reasoning limitations in LLMs. Methodologies like Retrieval-Augmented Generation (RAG) and Knowledge Graph (KG) injection significantly enhance factual accuracy and reduce hallucination by grounding responses in verifiable, up-to-date information [12,71]. Prompting techniques (e.g., Chain-of-Thought) and internal knowledge management mechanisms further enable LLMs to better utilize and update their intrinsic knowledge [43,68]. These advancements extend to accelerating scientific discovery through automated extraction of insights from scientific literature, impacting fundamental NLP tasks like Named Entity Recognition (NER), Relation Extraction (RE), and Question Answering (QA) [38,41].
The foundational support for many of these NLP advancements is found in Knowledge Base Construction and Management (KBCM). This area focuses on the systematic creation, population, refinement, and continuous evolution of structured knowledge artifacts, primarily KGs and ontologies [3]. Techniques such as NER, RE, Entity Linking (EL), and Knowledge Graph Completion (KGC) are critical for building and enriching these knowledge bases, while advancements in ontology evolution, often driven by LLMs, ensure their adaptability to dynamic information environments [17]. Quality assurance, including validation and fusion, remains paramount to maintaining the integrity and trustworthiness of these knowledge assets [40].
Shifting to the critical domain of Model Extraction and Cybersecurity, knowledge acquisition plays a dual role. Offensively, frameworks demonstrate how proprietary machine learning models can be extracted from Machine Learning as a Service (MLaaS) platforms using optimized querying strategies, highlighting vulnerabilities related to intellectual property and privacy [15,45]. Defensively, specialized approaches like Pluvio leverage transfer learning and information bottleneck principles to perform assembly clone search across diverse architectures, crucial for identifying vulnerabilities and protecting intellectual property in codebases [24]. Secure deployment strategies and internal LLM security mechanisms are also vital for safeguarding AI systems [30,48].
In Robotics and Autonomous Systems, learning-based approaches are essential for overcoming the KAB in complex, dynamic physical environments. Reinforcement Learning (RL) frameworks, such as InfoBot and IBOL, leverage information-theoretic principles to acquire diverse and robust robotic behaviors for manipulation, locomotion, and human-robot interaction, particularly in settings with sparse rewards or for unsupervised skill discovery [35,56,64]. The development of “world models” and the autonomous abstraction of concepts are critical for advancing general AI in physical interaction [12].
Game Playing and Interpretable Reinforcement Learning serve as a benchmark for AI capabilities. Frameworks in this area not only enable superhuman performance, as exemplified by AlphaZero, but also focus on extracting and transferring “machine-unique concepts” to human experts, thereby bridging the human-AI knowledge gap and fostering interpretability in strategic decision-making [54]. This highlights the potential of AI to not only solve problems but also to advance human understanding through novel insights.
In Educational Technologies, Knowledge Tracing, and Student Modeling, the KAB is addressed by developing interpretable frameworks that provide actionable insights into students’ learning processes. Language Bottleneck Models (LBMs) utilize LLM encoder-decoder architectures to generate human-understandable natural-language summaries of student knowledge states, facilitating personalized learning and assessment [50]. Complementary approaches, such as Multi-View Knowledge Models (MVKM), dynamically track knowledge acquisition from diverse learning resources, modeling the nuances of learning and forgetting [22].
Beyond these core areas, Other Domain-Specific Applications showcase the pervasive utility of knowledge acquisition. In clinical and healthcare, solutions range from automated event detection in Electronic Health Records (EHRs) to expert prior elicitation for predictive modeling and the construction of robust medical KGs [3,19,21]. Industrial operations benefit from trusted knowledge extraction for operations and maintenance intelligence, while socio-economic and environmental monitoring leverage machine learning for high-resolution poverty mapping from satellite imagery [39,48]. Knowledge-based Visual Question Answering (KVQA) integrates multimodal data with external knowledge for robust reasoning [61].
Finally, the pursuit of Cross-Domain and Versatile Knowledge Acquisition represents a grand challenge. Frameworks employing transfer learning, advanced LLMs, and agentic problem-solving (e.g., Agent KB) aim to enable systems to adapt to unfamiliar data distributions and architectural environments without extensive re-engineering [24,33,68]. The use of universal thief datasets, multilingual semantic networks (like BabelNet), and graph-based RAG further underscore efforts to build generalizable and adaptable knowledge systems across diverse modalities and fields [10,15,71].
Despite these profound advancements, several integrated challenges persist across these application domains. A recurring issue is the Ineffective Knowledge Utilization or Knowledge Complexity Mismatch, where models, particularly LLMs, struggle to genuinely leverage or effectively integrate specialized domain knowledge, leading to limited performance gains even when such knowledge is available [7]. The demand for Interpretability and Explainability remains critical, particularly in sensitive areas like healthcare, education, and policy, where predictions need to be auditable and provide actionable scientific insights beyond mere accuracy [39,50]. Challenges in Scalability, Versatility, and Generalizability are evident in the difficulty of transferring learned skills across truly disparate contexts (e.g., the sim-to-real gap in robotics) or adapting to dynamic environments without substantial re-adaptation [24,64]. This is further complicated by the “knowledge acquisition utilization gap” under distributional shifts, where models fail to generalize the application of their knowledge to novel relational patterns [53].
Data Scarcity and Quality continue to be fundamental bottlenecks, particularly for rare events, novel facets, or specialized domains, necessitating efficient annotation strategies, robust handling of noisy data, and comprehensive uncertainty management in KG construction [25,55]. Furthermore, LLM-specific limitations such as hallucination, semantic loss during KG-to-text conversion, high computational costs, context length restrictions, and the phenomenon of “knowledge entropy decay” pose significant challenges to their robustness and trustworthiness across applications [12,69]. Finally, the Ethical and Legal Implications of AI applications, particularly concerning model extraction, intellectual property rights, data privacy, and the responsible deployment of trusted knowledge extraction systems, are paramount considerations that require continuous attention and robust safeguards [15,48].
Future research must prioritize developing hybrid AI systems that effectively integrate symbolic knowledge representation with sub-symbolic machine learning models to bridge the Knowledge Complexity Mismatch. Advancements are needed in quantifying and enhancing the robustness of cross-domain transfer mechanisms, devising evaluation benchmarks that rigorously test versatility, and addressing the knowledge acquisition utilization gap under distributional shifts. Simultaneously, focus must remain on improving the interpretability, explainability, and accountability of AI decisions, particularly in high-stakes environments, while developing scalable and cost-effective strategies for high-quality data acquisition and uncertainty management. Progress in these integrated areas will be crucial for realizing truly intelligent, reliable, and interpretable AI systems that effectively overcome the knowledge acquisition bottleneck across a growing spectrum of real-world applications.
6.1 Natural Language Processing (NLP) and Generative AI
The confluence of Natural Language Processing (NLP) and Generative AI has profoundly transformed information interaction, yet its full potential is often constrained by a critical “knowledge acquisition bottleneck” [12,20]. This section delves into the synergistic relationship between knowledge acquisition strategies and their application in enhancing Generative AI systems, particularly Large Language Models (LLMs), as well as foundational NLP tasks and the extraction of scientific knowledge. It synthesizes diverse frameworks and algorithms that aim to integrate, leverage, and manage explicit knowledge, thereby addressing core challenges such as factual inconsistency, reasoning limitations, and the dynamic nature of real-world information.
A foundational theoretical framework underpins this domain, positing that the implicit, parametric knowledge inherent in LLMs is insufficient for consistently reliable and accurate generative outputs. LLMs frequently exhibit a “utilization gap,” where despite potentially storing relevant information, they struggle to apply it effectively or reliably, leading to issues like hallucination and factual inaccuracies [30,53]. To counteract this, the framework advocates for externalizing and structuring knowledge, often in the form of Knowledge Graphs (KGs) and ontologies. This structured knowledge provides verifiable, dynamic, and semantically rich context, moving systems beyond purely data-driven paradigms towards more robust, knowledge-driven intelligence. The core objective is to ensure that LLMs are not only capable of generating fluent text but also grounded in accurate, up-to-date, and contextually relevant information, thereby overcoming the limitations of static training data and improving trustworthiness.
A spectrum of methodologies has emerged to integrate external knowledge into NLP systems and Generative AI:
- Retrieval-Augmented Generation (RAG): These systems dynamically retrieve relevant information from external knowledge bases during the generation process, significantly enhancing factual accuracy and reducing hallucination by providing up-to-date and contextually appropriate facts [12,30]. Advanced RAG approaches, such as graph-based frameworks (e.g.,
GRAIL,RoG), further improve reasoning by utilizing structured graph information to guide LLMs through complex multi-hop queries, achieving superior accuracy and interpretability [63,71]. - Knowledge Graph (KG) and Ontology Injection: This strategy explicitly integrates structured semantic knowledge from KGs and ontologies into LLMs, either during pre-training or fine-tuning, at various architectural layers [12,74]. This infusion provides LLMs with a richer understanding of entities and their interconnections, going beyond mere statistical correlations. Ontologies, such as KNOW, are specifically designed to ground responses in explicit facts, addressing hallucination and enabling personalized content generation for applications like personal AI assistants [36].
- Prompting and Internal Knowledge Elicitation: This category leverages advanced prompt engineering techniques, including Chain-of-Thought (CoT) and Graph of Thoughts (GoT), to stimulate reasoning and elicit latent knowledge from LLMs through logical descriptions and structured prompts. Methods like
AutoPromptautomatically generate optimized prompts to access inherent knowledge, enabling LLMs to perform knowledge-intensive tasks more accurately and efficiently without extensive fine-tuning [43]. - Internal Knowledge Management and Acquisition: This area focuses on improving LLMs’ intrinsic capabilities for acquiring, updating, and retaining knowledge. Frameworks like
Self-Tuningempower LLMs to continually learn and update new factual knowledge, thereby improving factual accuracy and reasoning while reducing hallucination and increasing trustworthiness across various model architectures [68].
These methodologies are often interdependent, with Information Extraction (IE) techniques serving as the bedrock for creating the structured knowledge (e.g., KGs) that fuels both KG injection and RAG systems [3,9].
The impact of these knowledge acquisition advancements is multi-faceted across NLP and Generative AI:
- Enhanced Generative AI Capabilities: Knowledge augmentation directly improves factual accuracy and reduces hallucination in LLMs, as demonstrated by superior performance in QA and fact retrieval benchmarks [1,71]. It also leads to enhanced reasoning, personalized content generation, and domain-specific expertise, empowering LLMs in fields from finance to biomedicine [5,36,63].
- Accelerated Scientific Discovery and Dissemination: Automated extraction tools like
AxCELLandMatSKRAFTtransform vast amounts of unstructured scientific literature into structured knowledge, populating leaderboards, identifying research trends, and democratizing access to scientific information for both experts and non-scientific audiences [2,41,65]. Domain-specific KGs and fine-tuned LLMs enable complex scientific question answering and hypothesis generation, fostering “dark knowledge”—insights unknown to humans but discoverable by machines [30,71,75]. - Improved General NLP Tasks: Fundamental tasks such as Named Entity Recognition (NER), Relation Extraction (RE), Entity Linking (EL), and Word Sense Disambiguation (WSD) significantly benefit from structured knowledge and enhanced data efficiency [10,38]. Knowledge-enhanced Question Answering (QA) systems leverage KGs and RAG for more accurate and interpretable answers, even for complex multi-hop queries [71,74]. These advancements directly address the
data scarcityandmanual effortchallenges in traditional NLP by reducing the need for extensive manual annotation [57].
Despite these significant advancements, the field faces several critical challenges and remains “relatively immature” [74]. A pervasive issue is Ineffective Knowledge Utilization, where knowledge injection methods often fail to genuinely leverage specific external knowledge, leading to limited performance gains without careful “purification” or conceptualization of knowledge [7]. LLMs continue to grapple with hallucination and semantic loss when transforming structured KGs into textual responses [12]. The quality and noise of external knowledge sources, particularly from the web, pose ongoing challenges for maintaining factual accuracy and reliability [20]. Other limitations include scalability issues in knowledge extraction, higher uncertainty in unsupervised Open Information Extraction (OpenIE) systems, and the limited interpretability of automatically generated prompts, which can obscure insights into model behavior and robustness [43,55]. The phenomenon of “knowledge entropy decay” during pretraining also highlights challenges in consistent knowledge acquisition and retention in dynamic environments [69].
Future research must prioritize developing more robust and authentic mechanisms for knowledge acquisition, updating, and genuine integration into LLMs, moving beyond superficial alignment [12]. This includes enhancing explainability and interpretability of AI models, particularly for applications requiring public and policy adoption beyond mere predictive accuracy [39]. Addressing the inference overheads of multi-stage retrieval methods, integrating diverse scientific languages (e.g., mathematical expressions, chemical notations), and expanding extraction capabilities to capture complex scientific insights like causal relationships and experimental protocols are crucial [12,20]. Finally, providing quantifiable confidence scores and provenance for LLM-generated facts is vital to increase trustworthiness and usability, especially in tasks like KG construction [55]. Progress in these areas will solidify the role of knowledge-enhanced NLP and Generative AI in delivering reliable, intelligent, and transparent systems.
6.1.1 Knowledge-Enhanced LLMs and Generative AI
The integration of external knowledge into Large Language Models (LLMs) represents a pivotal advancement in overcoming the inherent limitations of purely data-driven models, particularly concerning factual accuracy, reasoning, and the dynamic nature of real-world information [12,73]. This section analyzes various frameworks, algorithms, and applications that leverage knowledge augmentation to enhance LLMs for generative AI use cases, offering a comprehensive understanding of their underlying assumptions, architectural choices, and domain-specific adaptations.
A primary motivation for knowledge-enhanced LLMs is to mitigate issues of factual inconsistency and hallucination, which are pervasive challenges in generative AI [20,30]. LLMs, while possessing extensive parametric knowledge, often demonstrate “unreliability” and a “utilization gap” in consistently applying this knowledge, affecting the dependability of their generative outputs [53]. Knowledge augmentation addresses this by grounding LLM responses in verifiable, structured information.
Strategies for Knowledge Augmentation
Knowledge Enhancement Strategies for LLMs in Generative AI
| Strategy Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Retrieval-Augmented Generation (RAG) | Dynamically retrieves info from external KBs during generation. | Enhances factual accuracy, reduces hallucination, real-time updates. | GRAIL (graph-based RAG), R1-Searcher++ (dynamic internal/external switch), IRCoT, ReAct (web-enhanced). | Scalability of external memory, noisy/low-quality sources, inference overhead. |
| Knowledge Graph (KG) & Ontology Injection | Infuses structured knowledge from KGs/ontologies into LLMs. | Richer understanding of entities, interconnections, reduces hallucination. | KeLM Corpus (Wikidata verbalization), GLM (KG-guided pre-training), KNOW (ontology grounding), Evo-DKD (autonomous ontology evolution). | Semantic loss, interference between signals, “ineffective utilization,” architectural mismatch. |
| Prompting & Internal Knowledge Elicitation | Leverages advanced prompts to stimulate reasoning & elicit knowledge. | Activates latent knowledge, improves reasoning, reduces fine-tuning. | AutoPrompt (optimized prompts), Chain-of-Thought (CoT), Tree of Thoughts (ToT). | Prompts can be uninterpretable, brittleness, computational intensity of complex prompts. |
| Internal Knowledge Management & Acquisition | Improves LLMs’ intrinsic capabilities for acquiring/retaining knowledge. | Continuous learning, dynamic updates, reduced catastrophic forgetting. | Self-Tuning (self-teaching), Knowledge Entropy “resuscitation,” DWML (efficient pretraining). | “Knowledge entropy decay” limits new acquisition, potential for knowledge conflicts. |
Various strategies have emerged to augment LLMs, broadly categorized by their approach to integrating external knowledge:
-
Retrieval-Augmented Generation (RAG): RAG systems dynamically retrieve relevant information from external knowledge bases during the generation process, enhancing factual accuracy and reducing hallucination by providing up-to-date and contextually appropriate facts [12,30]. Architecturally, RAG often involves a retriever module that fetches documents or snippets, and a generator that synthesizes a response conditioned on both the input prompt and the retrieved information. Examples include methods that integrate Internet-Fewshot and multi-stage retrieval techniques like
IRCoTandReAct, allowing LLMs to access real-time web information for tasks requiring current knowledge [20]. Graph-based RAG frameworks, such asKeqing,GRAG,MindMap,EtD,RoG, andToG, further improve reasoning by utilizing structured graph information to guide LLMs through complex multi-hop queries, yielding accurate and interpretable responses [71]. GRAIL, for instance, interactively retrieves specific facts from knowledge graphs (KGs), achieving state-of-the-art performance in graph-based question answering with average accuracy improvements of 21.01% and $F_1$ improvements of 22.43% on datasets like WebQSP, CWQ, and MetaQA, while reducing retrieval redundancy by 88.56% compared to G-Retriever [63]. Similarly,R1-Searcher++employs reinforcement learning (RL) to incentivize dynamic knowledge acquisition, enabling LLMs to selectively switch between internal and external sources, achieving up to 4.3% higher performance and a 30.0% reduction in external retrieval calls over baselines, thus making knowledge utilization more efficient and cost-effective [27]. -
Knowledge Graph (KG) and Ontology Injection: KGs and ontologies provide structured, semantic knowledge that can be directly injected into LLMs at various architectural layers (input, intermediate, or objective) during pre-training or fine-tuning [12,74]. This explicit integration aims to infuse LLMs with a richer understanding of entities and their interconnections, going beyond simple word co-occurrences. The
KeLMCorpus, derived from verbalizing Wikidata, serves as a retrieval corpus for models like REALM, significantly improving factual accuracy on the LAMA Knowledge Probe (e.g., 12.94% gain on Google-RE) and open-domain QA tasks (e.g., 2.63% gain on NaturalQuestions) [1]. TheGLM(Graph-guided Masked Language Model) implicitly integrates KGs through entity masking and distractor-suppressed ranking during pre-training, yielding state-of-the-art accuracy on commonsense reasoning QA tasks like CommonsenseQA (74.1%) and SocialIQA (78.6%) [42]. Structured knowledge from KGs is also crucial for improving LLM performance in Knowledge Graph Completion (KGC) tasks, where generative LLMs like T5 and GPT-3.5-turbo achieve significant gains (e.g., 8.7% absolute H@1 increase for T5-small on Wikidata5M) when provided with 1-hop neighborhood information from KGs [49].Ontologies like KNOW [36] are designed to augment LLMs in real-world generative AI use cases, particularly for personal AI assistants. KNOW addresses hallucination, limited context windows, and enhances introspectability by grounding responses in explicit, structured facts about everyday human life, facilitating personalized content generation [36]. A novel approach, Evo-DKD, enables LLMs to autonomously evolve ontologies by adding new triples based on input, demonstrating real-time ontology growth that improves RAG system performance and enhances interpretability [17].
-
Prompting and Internal Knowledge Elicitation: Prompt engineering techniques, such as Chain-of-Thought (CoT), Tree of Thoughts (ToT), and Graph of Thoughts (GoT), leverage logical descriptions and KGs to stimulate reasoning and produce more sophisticated generative outputs [12]. AutoPrompt, for instance, automatically generates optimized prompts to elicit inherent knowledge from LLMs like RoBERTa, achieving high accuracy in tasks like sentiment analysis (91.4% on SST-2) and fact retrieval (43.34% P@1 on LAMA) without fine-tuning, demonstrating the LLM’s capacity to perform knowledge-intensive tasks more accurately and efficiently in low-data regimes [43].
-
Internal Knowledge Management and Acquisition: Research also focuses on improving LLMs’ intrinsic knowledge acquisition and retention mechanisms. The
Self-Tuningframework allows LLMs to acquire and update new knowledge, significantly improving factual accuracy (e.g., 11.5% EM increase on open-ended generation) and reasoning on NLI tasks, contributing to reduced hallucination and increased trustworthiness across various LLM architectures [68]. Insights into “knowledge entropy decay” highlight the importance of strategic continual learning and “resuscitation” methods to optimize knowledge acquisition and retention, preventing catastrophic forgetting and enabling more dynamic updates [69]. Furthermore, the DWML framework facilitates efficient pretraining and distillation of smaller LLMs by allowing “student” models to collectively learn, enhancing capabilities for resource-constrained edge systems in tasks like syntactic understanding (BLiMP) and general knowledge (EWoK) [8].
Practical Implications and Benefits
Knowledge augmentation techniques lead to more robust and knowledgeable AI systems by overcoming purely data-driven limitations:
- Improved Factual Accuracy and Reduced Hallucination: By integrating explicit knowledge, systems like RAG and KG-enhanced LLMs significantly reduce the prevalence of factual errors and hallucinations, as evidenced by improved performance in QA and fact retrieval benchmarks [1,71].
- Enhanced Reasoning Capabilities: Graph-based approaches, in particular, empower LLMs to perform complex, multi-hop reasoning tasks that are traditionally challenging, as demonstrated by GRAIL and other graph-enhanced RAG models [63,71]. The DKA framework also demonstrates enhanced domain-specific knowledge utilization for complex tasks like Knowledge-based Visual Question Answering (KVQA), achieving 62.1% accuracy on OK-VQA by providing precise and aligned external knowledge to the LLM [61].
- Personalized and Controllable Generation: Ontologies like KNOW, with their focus on everyday human life, enable personalized content generation for personal AI systems [36]. Moreover,
Concept Bottleneck LLMs(CB-LLMs) introduce intrinsic interpretability, allowing users to steer generative outputs by activating specific concept neurons, thus enabling controlled generation and toxicity reduction (e.g., 0.9996 accuracy in detecting harmful queries and 0.9137 steerability score) [32]. - Domain-Specific Expertise: Frameworks like
Skigenerate high-quality structured data from raw domain knowledge, addressing domain knowledge deficits and improving factual accuracy in specialized fields such as finance and biomedicine [5].KnowMapdynamically constructs environmental and experiential knowledge to augment LLMs for embodied AI tasks, leading to significant improvements (e.g., 17.71% forgpt-4-turboin ScienceWorld) in specialized text-based environments and offering a cost-effective alternative to large model fine-tuning [44]. TheKnowledge AIframework similarly applies fine-tuned LLMs for understanding and extracting scientific knowledge, improving summarization, text generation, and QA in scientific contexts [2]. - Cost-Effective Expert Interaction and Reinforcement Learning: The PU-ADKA framework exemplifies cost-effective domain knowledge acquisition in sensitive fields like drug discovery. It leverages Multi-Agent Reinforcement Learning to optimize the selection of questions and experts within budget constraints, demonstrating significant performance gains (Win Rate and Length-Controlled Win Rate) over baselines with human-involved validation [4]. This highlights how strategic expert interaction, guided by RL, can efficiently enhance LLMs.
Limitations and Future Directions
Despite significant advancements, the field of knowledge-enhanced LLMs is still “relatively immature,” facing several limitations [74]. One major challenge is the inherent “unreliability of parametric knowledge” and the “utilization gap” in LLMs, which means models may store knowledge but fail to retrieve or apply it consistently [53]. Knowledge conflicts, where LLMs favor outdated internal knowledge over provided context, can still impact factual accuracy, especially in dynamic environments where information changes rapidly [20].
The quality and noise of external knowledge sources, particularly web content, pose ongoing challenges for Internet-enhanced LLMs [20]. The interpretability of prompts generated by methods like AutoPrompt remains limited, making it difficult to understand the underlying reasoning [43]. Furthermore, a critical analysis reveals that many existing knowledge injection frameworks suffer from Ineffective Knowledge Utilization if the external knowledge is not sufficiently “purified” or conceptual, leading to limited performance gains without careful curation [7]. This highlights the need for cleaner, more abstract knowledge, as demonstrated by the 4% accuracy enhancement in ChatGPT with conceptual knowledge injection [7].
Future research should focus on developing more robust mechanisms for knowledge acquisition and updating, ensuring genuine and authentic knowledge integration rather than superficial alignment [12]. Addressing the inference overheads of multi-stage retrieval methods is crucial for real-time generative applications [20]. Enhancing the generation of multi-modal content to align more closely with human cognitive concepts and intentions also requires stronger knowledge constraints [12]. Lastly, methods for providing quantifiable confidence scores and provenance for LLM-generated facts, especially in KG construction, are vital to increase trustworthiness and usability [55]. Progress in these areas will further solidify the role of knowledge-enhanced LLMs in shaping reliable and intelligent generative AI systems.
6.1.2 Scientific Knowledge Extraction and Dissemination
Scientific knowledge, primarily disseminated through academic publications, represents an invaluable yet often unstructured reservoir of information crucial for research advancement. The knowledge acquisition bottleneck in scientific domains is characterized by the sheer volume and complexity of scholarly literature, necessitating automated frameworks and algorithms for efficient extraction and dissemination. These tools serve the dual purpose of accelerating scientific discovery for researchers and making complex information accessible to non-scientific audiences [55,74]. The process typically involves Information Extraction (IE) techniques to transform unstructured scientific text into structured data, frequently represented as Knowledge Graphs (KGs) [3,55].
Scientific Knowledge Extraction & Dissemination Applications
| Application Area | Framework / Tools | Core Mechanisms | KAB Addressed / Benefit | Limitations / Challenges |
|---|---|---|---|---|
| Non-Scientific Audience / Public | Knowledge AI Framework | Fine-tuned BART/LED (summarization), distilgpt2 (text gen), SciBERT/FLAN-T5 (QA), NER models. | Democratizes access to scientific info, accelerates discovery. | Primarily serves researchers, not general public, requires domain adaptation. |
| Scholarly Information Extraction | AxCELL | LaTeX source parsing, ULMFiT classifiers, Bayesian inference. | Populates leaderboards, tracks research progress precisely. | Relies on LaTeX, not for generic PDFs, focuses on performance metrics. |
| EneRex | Weakly-supervised IE, NER for code, datasets, methods. | Identifies research trends, broad overview of research ecosystem. | Broader overview, not always specific quantitative insights. | |
| SciNLP-KG | BERT-based NER/RE, KG construction for TDM entities. | Facilitates automatic leaderboards, structures NLP research. | Specialized for NLP, may not capture broader scientific insights. | |
| Materials Science Discovery | MatSKRAFT | GNNs for tables, constraint-driven learning, data augmentation. | Large-scale knowledge extraction from tables, identifies rare properties, democratizes access. | Domain-specific, complex rule engineering, limited generalizability. |
| Biomedical Text Mining | HYPE (Hypoglycemia), KRDL, GPT-3 IE, BioBERT, SciBERT, Ski, StructSense, PU-ADKA | CNNs/LSTMs for event detection, cross-sentence RE, KGE, LLM-based IE, Active Learning for expert interaction. | Automates knowledge curation, speeds up database population, improves clinical predictive capabilities. | Knowledge Complexity Mismatch, Ineffective Utilization, Data Scarcity, interpretability of numerical values. |
To facilitate understanding for a “non-scientific audience,” several frameworks leverage advanced Natural Language Processing (NLP) models. The “Knowledge AI” framework, for instance, fine-tunes various NLP models for diverse applications. It utilizes fine-tuned BART and LED models for scientific article summarization, generating concise or comprehensive overviews that effectively convey scientific goals and methodologies to broader audiences [2]. Scientific text generation is addressed using fine-tuned distilgpt2, capable of producing contextually relevant scientific prose. Furthermore, scientific question answering (QA) systems, employing models like SciBERT (fine-tuned) and FLAN-T5 (zero-shot), enable non-experts to query scientific content and receive accurate answers without requiring deep domain expertise. Named Entity Recognition (NER) models are also fine-tuned to identify and classify scientific entities within computer science and biology texts, crucial for structuring and indexing information. The overarching goal of these applications is to “democratize access to scientific information” and “accelerate scientific discovery” by improving communication across various user groups [2]. Similarly, in the domain of poverty and welfare estimation, research aims to disseminate scientific insights into the multi-dimensional nature of poverty to social scientists, economists, and policymakers. This necessitates improved interpretability and explainability of machine learning models to ensure “wider dissemination and acceptance” beyond specialized groups [39].
Automated scholarly information extraction significantly impacts research workflows and knowledge synthesis. AxCELL is designed for the automatic extraction and dissemination of scientific knowledge from machine learning papers, addressing the challenge of tracking progress and comparing methodologies across an overwhelming number of publications [41]. This system extracts (task, dataset, metric name, metric value) tuples from LaTeX source files, populating leaderboards on platforms like paperswithcode.com. Its architectural choice of processing LaTeX provides a structural advantage for precise data extraction, which is then used to create a comprehensive resource, making comparisons easier and more reliable for researchers, thus implicitly accelerating research [41].
Another critical framework, EneRex, extracts six key facets from full-text scholarly articles: source code links, dataset usage, objective tasks, methods, computing resources, and programming languages/libraries [51]. Applied to a large arXiv CS dataset, EneRex facilitates understanding emerging technologies and identifying research and development trends. For instance, it reveals trends in GitHub usage for code sharing, dataset popularity (e.g., MNIST), and the adoption rates of deep learning frameworks like TensorFlow and PyTorch. These insights are invaluable for “analysts and policymakers to identify key trends” [51]. While AxCELL focuses on quantitative performance metrics for direct comparison, EneRex provides a broader, qualitative overview of research ecosystem trends. Both contribute to knowledge synthesis by structuring vast amounts of scholarly information, although their primary target audience remains domain experts rather than the general public. Relatedly, the SciNLP-KG framework focuses on extracting “tasks, datasets, and metrics” from NLP papers to build structured Knowledge Graphs, aiming to “facilitate automatically constructing scientific leaderboards for the NLP community” [11]. This specific focus, while valuable, implies a limitation in capturing broader scientific insights such as methodologies or research problems.
In the realm of materials science, MatSKRAFT provides a unique contribution to scientific discovery by performing “large-scale materials knowledge extraction from scientific tables” [65]. MatSKRAFT processes approximately 69,000 tables from over 47,000 research publications, resulting in a comprehensive database of materials science knowledge with over 535,000 entries. This extensive extraction supports the generation of Materials Selection Charts (Ashby plots), multi-property screening for complex design criteria, identification of rare materials with unusual property combinations (e.g., high glass transition temperature with low thermal expansion occurring in 0.19% of cases), and temporal analysis of research trends in various application domains like Coatings/Barriers and Optical/Photonics. By structuring quantitative composition-property data, MatSKRAFT effectively “democratizes access to scientific information and transforms serendipitous materials exploration into systematic, data-driven processes” [65]. The theoretical foundation here lies in structured data extraction from tabular layouts, a more precise but often challenging task than general text IE.
Beyond these, various domain-specific applications highlight the pervasive utility of scientific knowledge extraction. In biomedicine, systems extract genetic mutation information from MEDLINE citations to populate structured databases like COSMIC, thereby accelerating the transfer of knowledge into actionable data for researchers and clinical pipelines [25]. Frameworks like Knowledge-Rich Deep Learning (KRDL) for “precision oncology machine reading” automate knowledge curation by performing cross-sentence relation extraction (e.g., drugs, genes, mutations) and entity linking, significantly outperforming state-of-the-art systems in recall and precision for relation extraction [16]. GPT-3 powered IE systems are also employed for biomedical information extraction, tackling NER and relation extraction tasks from PubMed/MEDLINE abstracts [18]. Graph-based Retrieval-Augmented Generation (RAG) models, such as DALK, ATLANTIC, and KGP, build domain-specific KGs from scientific literature, such as Alzheimer’s Disease research, and leverage structural information to answer complex scientific questions, thereby enhancing faithfulness and relevance [71]. The SAC-KG framework, demonstrated in the “rice domain,” constructs KGs of over one million nodes from specialized texts, achieving 89.32% precision and 81.25% domain specificity by iteratively building a multi-level KG with Generator, Verifier, and Pruner components, outperforming previous methods [66]. In neuroscience, StructSense employs an agentic framework with human-in-the-loop (HIL) evaluation for schema-based extraction from clinical assessments, metadata extraction of scientific resources, and NER term extraction from full-text articles. It shows that HIL significantly enhances model performance, with Claude-Sonnet 3.7 achieving near-perfect recall (1.00) in schema-based extraction with HIL [70].
The theoretical foundations of these systems often rely on a combination of classical Information Extraction (IE) techniques, deep learning models (e.g., BERT, GPT variants), and Knowledge Graph (KG) methodologies. Architectural choices vary from pipeline-based approaches (e.g., AxCELL’s LaTeX processing) to end-to-end neural models and agentic frameworks. Domain-specific adaptations are crucial, ranging from specialized biomedical language models (e.g., BioBERT, SciBERT) to tailored entity and relation schemata for fields like materials science or requirements engineering [6,16]. The underlying assumption is that scientific knowledge, despite its complexity, can be formalized into structured representations, enabling computational processing and reasoning. LLMs are also increasingly leveraged for tasks like “Scientific Hypotheses Generation,” proposing novel hypotheses from research goals and corpora, moving beyond mere commonsense knowledge [75]. Furthermore, the concept of “dark knowledge” or “knowledge unknown to human” but “known to machine” (UH, KM) is emerging, exemplified by AI systems excelling in gene prediction and structural elucidation of proteins, accelerating scientific discovery by identifying patterns beyond human processing capacity [30].
A critical assessment reveals several limitations and areas for improvement. A significant challenge in scientific knowledge extraction is the higher uncertainty inherent in IE methods, particularly Open IE, which is problematic in domains where precision is paramount [55]. Text heterogeneity further complicates consistent extraction. While many systems demonstrate high performance within specific tasks or entity types, they often struggle with a broader scope; for example, SciNLP-KG focuses on TDM entities but does not explicitly capture methods or research problems [11]. A recurring critique is the lack of explicit strategies for disseminating extracted scientific knowledge to a general public or varied domain experts in an accessible manner, with many systems primarily serving researchers [2,25,66]. The observed “Ineffective Knowledge Utilization” bottleneck, where injecting domain-specific factual knowledge does not reliably improve performance over random knowledge in NER tasks, highlights a gap in how models integrate and leverage specialized KGs [7].
Future research needs to address the explicit incorporation of expert-validated uncertainty quantification and the accurate representation of “knowledge deltas” (e.g., vagueness, fuzziness) prevalent in scientific discourse [55]. Enhancing the explainability and interpretability of AI models is paramount, especially for applications aiming for wider public and policy adoption, where high predictive accuracy alone is insufficient for true scientific discovery and acceptance [39]. Furthermore, while current systems excel in specific extraction tasks, a “completely automatic KG construction is not yet in reach,” necessitating continued efforts in automation and scalability to reduce reliance on manual or semi-manual steps [3]. The integration of diverse scientific languages, such as mathematical expressions and chemical notations, into machine-processable forms for LLMs remains a challenge [12]. Finally, expanding extraction capabilities beyond entities and relations to encompass complex scientific insights like experimental protocols, causal relationships, and nuanced data interactions across modalities is essential for advancing the full potential of scientific knowledge extraction and dissemination.
6.1.3 General NLP Tasks and Textual Information Extraction
Advancements in knowledge acquisition have profoundly impacted the performance and generalizability of Natural Language Processing (NLP) models across a spectrum of language understanding tasks, particularly those involving textual information extraction. These advancements address the knowledge acquisition bottleneck (KAB) by facilitating the creation of structured knowledge from unstructured text, enhancing model reasoning, and reducing reliance on labor-intensive manual annotation.
General NLP Tasks Enhanced by Knowledge Acquisition
| NLP Task Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Fundamental Information Extraction | Converts unstructured text into structured data (NER, RE, EL). | Automates KG construction, reduces manual effort for IE. | DeepKE (NER, RE, AE), SAC-KG (LLM for OIE), Traditional IE (HMMs, CRFs). | Scalability of early methods, higher uncertainty in OpenIE, accuracy for specific domains. |
| Text Understanding | Enhances semantic comprehension beyond word co-occurrences. | Improves classification, abstraction, context-aware processing. | ESA (encyclopedic knowledge), Knowledge-based Topic Models, AutoPrompt (LLM elicitation), CB-LLMs (interpretable concepts). | LLM hallucination, semantic opacity of prompts, interpretability. |
| Word Sense Disambiguation (WSD) | Identifies correct meaning of words in context. | Improves semantic accuracy, aids language understanding. | Large-scale sense-annotated corpora (SemCor), OneSeC (Wikipedia categories). | Data scarcity for annotated corpora, noise from automatic annotation. |
| Question Answering (QA) | Provides structured factual context for accurate answers. | Enhances interpretability, handles complex multi-hop queries. | KG-based QA (G-Retriever, GraphRAG), KeLM Corpus (verbalized KG), Ski (synthetic Q&A), R1-Searcher++ (dynamic retrieval). | Hallucination, semantic loss from KG-text conversion, inference overheads for RAG. |
| Data Scarcity Mitigation | Optimizes data usage for model training. | Reduces annotation bottleneck, improves data efficiency. | Active Learning (Deep Bayesian AL), Ranking for Re-annotation. | Computational cost of retraining, sub-optimal OOD performance. |
A core area benefiting from improved knowledge acquisition is fundamental information extraction, including Named Entity Recognition (NER), Relation Extraction (RE), and Entity Linking (EL). Frameworks like DeepKE provide comprehensive toolkits for Knowledge Base Population (KBP), integrating deep learning models for NER, RE, and Attribute Extraction (AE) across diverse scenarios. DeepKE supports standard supervised settings, addresses low-resource (few-shot) scenarios to improve data efficiency, and extends to document-level and multimodal settings by incorporating visual features, all of which contribute to more comprehensive knowledge acquisition [38]. Similarly, the construction of Knowledge Graphs (KGs) itself heavily relies on sophisticated NLP pipelines for NER, EL, and RE, utilizing a range of dictionary-based, machine learning, and deep learning approaches, including LSTMs, CNNs, and pre-trained language models [3]. SAC-KG, for instance, leverages large language models (LLMs) to achieve state-of-the-art results in Open Information Extraction (OIE) benchmarks, surpassing traditional rule-based and other LLM-based methods by overcoming contextual noise and knowledge hallucination [66].
Knowledge acquisition methods also significantly bolster general text understanding tasks. Explicit Semantic Analysis (ESA), which maps text to a semantic space using encyclopedic knowledge, has demonstrated utility in tasks such as short text classification and clustering by leveraging external knowledge beyond simple word co-occurrences [72]. Knowledge-based topic models, like OHLDA and KB-LDA, further improve text classification by integrating ontology information [72]. In the context of LLMs, approaches like AutoPrompt can elicit knowledge for tasks such as sentiment analysis, natural language inference (NLI), and relation extraction, enabling MLMs to achieve competitive performance without explicit fine-tuning, thus reducing reliance on labor-intensive annotation [43]. The Self-Tuning framework enhances LLMs’ factual accuracy in open-ended generation and NLI by improving knowledge acquisition, memorization, and reasoning capabilities across various domains [68]. Interpretability in these models is addressed by Concept Bottleneck LLMs (CB-LLMs), which provide explicit and human-understandable concept detection for text classification and generation, offering intrinsic interpretability for robust NLP systems [32].
A crucial area for improved language understanding is Word Sense Disambiguation (WSD). Knowledge acquisition methods are particularly vital here, especially those facilitating the creation of large-scale sense-annotated corpora. These corpora, such as SemCor and SemEval datasets, serve as indispensable training data and benchmarks for supervised WSD systems, enabling the learning of effective sense embeddings and improving disambiguation performance. Even noisier, automatically generated annotations can enhance semi-supervised WSD systems due to their broader coverage [10]. For example, the Princeton WordNet Gloss Corpus, a sense-annotated resource, has proven useful for semantic similarity and domain labeling, alongside WSD [10].
The broader implications of these advancements for general information extraction and management are substantial. Information Extraction (IE) is recognized as a fundamental building block for complex NLP tasks such as knowledge base construction, text summarization, and Question-Answering (QA) systems [9]. Methodologies from knowledge acquisition enable diverse applications, including extracting user profiles from social media, automating email processing, streamlining resume filtering, populating databases from classified advertisements, and enhancing customer service by structuring communications [9]. Knowledge Graphs (KGs) play a pivotal role in these knowledge-intensive tasks, underpinning semantic search, conversational interfaces, and natural language generation by providing structured factual context [74]. For instance, KGValidator utilizes LLMs and Retrieval-Augmented Generation (RAG) for fact verification, a foundational task for many downstream NLP applications [40]. Tools like DeepKE are explicitly designed for KBP, providing off-the-shelf models for entity and relation extraction that can be applied to plain texts for real-time visualization of knowledge graphs [38].
In Question Answering (QA), the integration of knowledge acquisition techniques has been transformative. KGs provide a structured source of common-sense knowledge, yielding more interpretable answers in both textual QA and KBQA scenarios [74]. Methods like G-Retriever, SR, and GraphRAG improve KGQA by formulating subgraph retrieval as optimization problems and leveraging GNNs and LLMs for fine-tuned reasoning [71]. The KeLM Corpus, generated by verbalizing KG knowledge, demonstrably enhances factual knowledge recall in QA tasks (NaturalQuestions, WebQuestions) and LAMA knowledge probes [1]. Similarly, Ski transforms raw documents into question-augmented representations, significantly improving LLMs’ performance on QA benchmarks like HotpotQA and Natural Questions by automating the generation of high-quality synthetic QA data, thereby reducing the need for manual annotation [5]. For complex multi-hop QA, the R1-Searcher++ framework employs reinforcement learning to dynamically balance internal knowledge and external retrieval, achieving significant performance gains while reducing retrieval costs by up to 4.3% over baselines [27]. In domain-specific contexts, fine-tuned LLMs demonstrate improved scientific QA, summarization, and NER performance, adapting general NLP models for specialized knowledge extraction and understanding [2].
The goal of developing more generalizable and robust NLP models across various language understanding tasks is often achieved by addressing the data scarcity and manual effort associated with traditional annotation. Active learning strategies, such as Deep Bayesian Active Learning, have shown significant efficiency gains in tasks like sentiment classification, NER, and Semantic Role Labeling (SRL), achieving comparable performance to full datasets with as little as 20% of the labeled data for NER tasks [57]. Similarly, ranking methods that optimize human re-annotation efforts can substantially reduce the performance gap in NER models for domain-specific texts, such as biomedical mutation literature [25]. The use of pre-trained LLMs and instruction-driven tuning further improves generalization by enabling models to solve new NLP problems with unified input forms, as demonstrated by their strong capabilities in identifying entities and relations from text [12]. The FictionalQA dataset offers a controlled environment to study how LLMs acquire and internalize factual knowledge from diverse textual styles, revealing that varied documents lead to stronger factual transfer, informing how training data is curated for effective knowledge acquisition [60]. In specialized domains, however, general NLP tools without fine-tuning can perform significantly worse, highlighting the KAB in applying general-purpose models to domain-specific textual information extraction, such as in maintenance records [48].
When referencing measuring_the_knowledge_acquisition_utilization_gap_in_pretrained_language_models, it is crucial to clarify that the document retrieval task is used primarily for evaluating knowledge utilization, not as a standalone application of KAB-attacking techniques. The study’s core finding, the knowledge acquisition-utilization gap, implies that models may possess relevant information but struggle to apply it effectively without tailored fine-tuning or architectural modifications [53].
Despite these advancements, significant limitations and areas for improvement persist. A notable challenge highlighted by revisiting_the_knowledge_injection_frameworks is the “Ineffective Knowledge Utilization” problem, where current knowledge injection methods often fail to genuinely leverage specific external knowledge in tasks like NER, Entity Typing, Relation Classification, QA, and WSD, behaving as if they receive random inputs. This suggests a critical need for cleaner, more abstract knowledge representations to genuinely impact these tasks [7]. LLMs, while powerful, face challenges such as hallucination, semantic loss when converting structured KGs into text, and often do not always outperform traditional small models in tasks inherently reliant on structured knowledge [12,52]. The interpretability of automatically generated prompts, for instance, can be lacking, obscuring insights into model behavior and robustness [43]. Furthermore, the phenomenon of “knowledge entropy decay” during pretraining and continual learning hinders LLMs’ ability to acquire new knowledge and increases forgetting, impacting the robustness of NLP systems that need to adapt to evolving information [69]. Traditional IE systems also face limitations, including scalability issues in early methods and higher uncertainty in OpenIE systems due to their unsupervised nature [55]. Future research should focus on developing robust confidence propagation mechanisms through complex IE pipelines, addressing the persistent challenges of data quality in informal texts, and devising novel methods for knowledge representation that overcome the “Ineffective Knowledge Utilization” gap [7,9,55]. Furthermore, exploring how knowledge entropy can strategically fine-tune LLMs for better performance on new tasks and quantifying the reduction in manual annotation effort in real-world scenarios are critical avenues for advancing the field.
6.2 Knowledge Base Construction and Management
Knowledge Base Construction and Management (KBCM) is a foundational discipline for addressing the knowledge acquisition bottleneck, encompassing the systematic creation, population, refinement, and continuous evolution of structured knowledge artifacts such as knowledge graphs (KGs) and ontologies. This domain is critical for transforming raw data into actionable intelligence, enabling sophisticated reasoning and supporting a wide array of AI applications. The core objectives include ensuring the quality, completeness, consistency, and adaptability of knowledge bases in dynamic information environments [59].
The landscape of KBCM can broadly be categorized into two interconnected pillars: Knowledge Graph Enhancement and Ontology Evolution. Knowledge Graph Enhancement focuses on the practical aspects of building and populating KGs from diverse data sources, ensuring their accuracy, and continuously expanding their coverage. This involves sophisticated techniques for extracting structured information from unstructured and semi-structured texts, such as Named Entity Recognition (NER), Relation Extraction (RE), and Entity Linking (EL) [11,38]. Furthermore, critical processes like Knowledge Graph Completion (KGC) infer missing facts and links to address inherent incompleteness, often leveraging advanced models that integrate language context and neighborhood information [49]. Quality assurance and refinement, including entity resolution, data fusion, and automated validation, are paramount to maintaining the integrity and trustworthiness of KGs [40,59].
In parallel, Ontology Evolution addresses the challenge of maintaining and adapting the underlying schema and conceptual frameworks of knowledge bases. As domains change and new information emerges, ontologies require incremental updating, refinement, and extension to remain relevant and consistent [3]. Traditionally a manual and resource-intensive endeavor, recent advancements, particularly with Large Language Models (LLMs), are paving the way for more autonomous ontology management. LLMs exhibit strong capabilities in concept recognition and hierarchy construction, facilitating tasks such as ontological category expansion and attribute completion [12]. Frameworks like Evo-DKD exemplify this by employing dual knowledge decoding mechanisms that generate structured ontology edits alongside natural language justifications, incorporating rigorous validation modules to ensure consistency and contextual grounding [17]. This holistic approach moves towards closed-loop autonomous updating systems, crucial for scalable and dynamic knowledge environments.
The convergence of KG enhancement and ontology evolution is evident in shared objectives and the increasing reliance on advanced AI techniques. Both areas contend with fundamental Knowledge Engineering tasks such as ontology creation and refinement, data ingestion and transformation, data source integration, anomaly detection, and knowledge graph completion [59]. Large Language Models, in particular, are becoming central to both construction and management processes, offering powerful capabilities for automated extraction, generation, and reasoning. For instance, LLMs are utilized for automated KG construction, employing iterative Generator-Verifier-Pruner frameworks to build domain-specific KGs with high precision [66]. However, this also introduces shared challenges, notably the persistent issue of hallucination and ensuring the reliability and trustworthiness of LLM-generated knowledge, especially in specialized or long-tail domains [12].
Despite significant progress, several overarching limitations persist across KBCM. A primary challenge lies in the lack of holistic, integrated solutions that seamlessly combine continuous extraction, completion, and rigorous quality control throughout the entire lifecycle of knowledge bases [3]. Current methods often struggle with data source diversity, continuous update mechanisms, and effectively managing the inherent uncertainty associated with real-world data [55]. The reliability of LLM-based construction, while promising, still needs to overcome issues of hallucination and semantic loss, ensuring that autonomously generated knowledge is both accurate and semantically consistent [12].
Future research in Knowledge Base Construction and Management must focus on developing robust, integrated frameworks capable of dynamic, continuous adaptation. This entails advancing methodologies for uncertainty management, devising comprehensive quality assurance processes that span the entire knowledge lifecycle, and creating mechanisms for transparent versioning and change tracking in autonomously evolving knowledge bases [55]. Bridging the gap between theoretical models of symbolic evolution and practical, trustworthy computational implementations will be key to realizing truly intelligent and self-managing knowledge systems.
6.2.1 Enhancing Knowledge Graphs
The enhancement of Knowledge Graphs (KGs) is crucial for addressing their inherent incompleteness and ensuring their utility across various applications. This process involves sophisticated frameworks and algorithms that improve data quality, expand coverage, and enable adaptation to evolving information. Approaches to KG enhancement span initial construction, continuous quality assurance, and sophisticated completion mechanisms, often integrating advanced techniques from natural language processing and machine learning.
Knowledge Graph Enhancement Techniques
| Enhancement Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Construction & Population | Extracting structured info from diverse sources to fill KGs. | Improves completeness & coverage, automates data entry. | DeepKE (NER, RE, AE), SciNLP-KG (scientific IE), MatSKRAFT (table extraction), AutoPrompt (MLM-based IE). | Manual effort for initial rules/schema, data heterogeneity, accuracy for long-tail. |
| Quality Assurance & Refinement | Ensures accuracy, consistency, and canonical representations. | Maintains KG integrity, reduces errors, improves trustworthiness. | Entity Resolution (ER) & Fusion, KGValidator (LLM-based validation), SAC-KG (Verifier/Pruner), StructSense (alignment agent). | Scalability of ER, consistency in dynamic KGs, hallucination for LLM-based QA. |
| Knowledge Graph Completion (KGC) | Infers missing facts/links to address incompleteness. | Increases KG density, supports reasoning for unseen entities. | KG embeddings (TransE), Generative KGC (LLM + neighborhood info), GLM (KG-guided finetuning). | Verbalization limits graph-native neural networks, trustworthiness of predicted knowledge. |
| LLM-driven Automated Construction | LLMs extract/synthesize structured knowledge for KGs. | Reduces manual effort, enables flexible construction from diverse text. | SAC-KG (iterative G-V-P), LLMs for direct KG generation. | Hallucination, reliability issues, semantic loss during conversion. |
| Evolving KGs | Adapting KGs to evolving information and schemas. | Maintains relevance, supports continuous updates. | Evo-DKD (autonomous ontology evolution), KNOW (evolving commonsense ontology), KnowMap (dynamic fact updates). | LLM hallucination, ensuring consistency, scalability for complex ontology refactoring. |
A fundamental aspect of KG enhancement involves robust construction and population. Many studies focus on extracting structured information from unstructured and semi-structured texts to populate KGs, thereby improving their completeness and coverage [3,74]. Techniques such as Named Entity Recognition (NER), Relation Extraction (RE), and Entity Linking (EL) are core to this process [18,25,38,48]. For instance, DeepKE extracts entities, relations, and attributes using deep learning models (e.g., BERT, BART, RoBERTa), achieving high F1 scores and supporting schema-guided extraction, which ensures conformity for direct KG integration [38]. Similarly, the SciNLP-KG framework extracts domain-specific entities (Task, Dataset, Metric) and relations from scientific literature, providing rich, structured content for NLP KGs [11]. EneRex, designed for scholarly information extraction, enriches existing KGs by providing granular, domain-specific details like datasets and methods from scientific articles, aiming to develop a hierarchical taxonomy for better utility [51]. MatSKRAFT automatically constructs materials knowledge repositories by extracting composition-property pairs from scientific tables, significantly expanding coverage and identifying over 104,000 new material compositions not present in existing databases [65]. The concept of BabelNet, a multilingual semantic network integrating encyclopedic and lexicographic knowledge, serves as an enhanced KG by consolidating diverse sources [10]. AutoPrompt contributes to fact retrieval and relation extraction by generating optimized prompts for masked language models (MLMs), boosting precision-at-1 for BERT on the LAMA dataset to 43.34% and achieving 90.73% precision-at-1 on the T-REx dataset for relation extraction, thereby making MLMs more effective tools for KG construction [43].
Quality assurance and refinement are equally critical for maintaining KG accuracy and consistency. Entity Resolution (ER) and Fusion identify and merge matching entities, eliminating redundancies and inconsistencies to create canonical representations [3]. Systems like FlexiFusion and SAGA actively contribute to quality enhancement through fusion, data repair, and human curation [3]. The KGValidator framework specifically targets quality by automatically validating candidate triples, ensuring that only accurate and consistent information is integrated into KGs, which is vital for dynamic KGs like Wikidata [40]. Continuous quality monitoring and the application of DataOps principles are advocated to prevent poor quality data from compromising KG integrity [59]. Beyond mere extraction, the utility of KGs can be enhanced by refining how knowledge is presented for consumption by downstream models. For instance, creating “conceptual knowledge” by purifying and pruning raw KG information makes it more effective for Large Language Models (LLMs), significantly improving performance in tasks like relation classification [7]. StructSense leverages an alignment agent to map LLM-extracted entities to canonical concepts within an ontology database, ensuring semantic consistency and improving the accuracy and FAIR compliance of KGs [70].
Knowledge Graph Completion (KGC) algorithms are essential for resolving the inherent incompleteness of KGs by inferring missing information. Traditional KGC methods include Type Completion and Link Prediction, often leveraging KG embeddings like TransE for finding missing relations [3,9,74]. Newer approaches significantly enhance KGC through the integration of language models and neighborhood information. For example, a generative KGC method integrates transformer-based language models (T5, GPT-3.5-turbo) with explicit verbalized 1-hop neighborhood information of head entities [49]. This framework demonstrates significant improvements: on Wikidata5M, T5-small not pre-trained with neighbors achieves a Hits@1 of 0.327, a notable increase from 0.240 without neighbors. For inductive settings, T5-base with neighbors achieves state-of-the-art results, with Hits@1 of 0.116 on ILPC-large, outperforming IndNodePieceGNN (0.032) [49]. This architecture’s strength lies in its ability to predict links for unseen entities, crucial for dynamic KGs, and its scalability, as training is independent of KG size. Similarly, the Graph-guided Masked Language Model (GLM) enhances KGC by finetuning BERT/RoBERTa-based models to predict missing links and triple accuracy, achieving state-of-the-art results on datasets like WN18RR and CKBC [42]. The underlying assumption is that contextual linguistic patterns and local graph structures together provide sufficient evidence for inferring missing facts. While effective, the verbalization of complex graph structures might present a limitation compared to graph-native neural networks [49].
Frameworks leveraging LLMs for automated KG construction directly address the bottleneck of acquiring precise and dependable knowledge. SAC-KG is a notable example, designed for domain-specific KG construction. It employs LLMs as primary mechanisms for triple extraction, with a fine-tuned T5 model acting as a Pruner to guide KG growth, achieving a high precision of 89.32% in the “rice” domain and constructing KGs with over a million nodes [66]. This iterative framework—consisting of a Generator, Verifier, and Pruner—demonstrates how controlled LLM integration can significantly reduce manual effort in KG construction. Other LLM-driven approaches include generating KGs from natural language instructions in formats like RDF/OWL, synthesizing new knowledge, and enhancing KG management through automated query template generation and natural language to logical query parsing [12,52]. Generative Knowledge Graph Construction, using sequence-to-sequence models like T5 and BART, offers a unified approach to extract entities, relations, and events, tackling error propagation and poor adaptability in traditional pipelines [23]. However, despite these advancements, LLM-based construction faces challenges such as hallucination, where ChatGPT’s KG construction accuracy ranges from 70-80% for common domains to less than 20% for long-tail domains, often falling short of specialized small models in precision and reliability [12]. Semantic loss can also occur when converting structured graphs to text for LLM processing [12].
The ability to handle evolving information and ensure scalability is critical for maintaining relevant and up-to-date KGs. Evo-DKD offers a mechanism for autonomous ontology evolution, where new, validated triples are injected into the KG within a closed reasoning loop, enabling the KG to grow and improve without direct human intervention. Experiments show its Full Dual-Decoder mode outperforms single-mode baselines in precision of ontology updates and downstream task performance [17]. Similarly, KNOW, an ontology for neuro-symbolic AI, focuses on modeling human universals and social relationships, providing a foundation for scalable KG construction and maintenance through its open-source nature and support for RDF/JSON serializations [36]. KnowMap dynamically constructs and maintains environmental and experiential knowledge bases for task-specific adaptation, using observations and action feedback with a replacement mechanism to ensure currency and accuracy [44]. The framework of forgetting and consolidation for rule-based knowledge bases also highlights mechanisms for enhancing completeness, accuracy, and scalability by promoting reliable rules and demoting inconsistent ones, thereby managing an ever-growing knowledge base [67]. Uncertainty management in KG construction is also a critical area, with techniques for knowledge alignment, fusion, consistency checking, and Uncertainty-aware KG Embeddings (UKGE) applied in large-scale open KGs (e.g., Wikidata, DBpedia) and enterprise KGs (e.g., Bing KG, Facebook) [55]. However, many existing methods still struggle with noisy facts and inherent uncertainty, leading to accuracy and reliability issues [55].
It is important to differentiate between enhancing KGs and utilizing them. While some papers discuss LLMs leveraging KGs as external knowledge sources, their focus is on improving LLM performance rather than enhancing the KGs themselves. For instance, Knowledge Solver enables LLMs to search external KGs via prompting [20], and KeLM Corpus converts Wikidata into a natural language corpus to enhance LM pre-training, increasing the KG’s utility for LMs without directly improving the KG’s completeness or accuracy [1]. Similarly, measuring_the_knowledge_acquisition_utilization_gap_in_pretrained_language_models uses knowledge base facts as input but does not directly propose methods for enhancing KGs. CEGA focuses on acquiring GNN models for KG analysis rather than modifying the KG itself [45]. Moreover, discussions on “non-parametric knowledge storage” and “augmenting parametric knowledge in LLMs with non-parametric knowledge” acknowledge the importance of KGs but do not detail specific enhancement applications [30].
Limitations and Future Research: Despite significant progress, several limitations persist. Many KG construction projects are limited in data source diversity and lack support for continuous updates, hindering long-term enhancement [3]. The lack of holistic solutions to simultaneously improve multiple quality dimensions of KGs remains a challenge, as does the difficulty in identifying the origin of wrong values [3]. LLM-based KG construction, while powerful, is hampered by hallucination and reliability issues, particularly in specialized or long-tail domains [12]. Ensuring authentic knowledge and accountable reasoning from LLM-generated content is an open question [12]. Furthermore, the trustworthiness of predicted knowledge, especially when using KGC algorithms, needs careful consideration if the source KG itself contains quality issues [49]. Future research should focus on developing integrated enhancement strategies that combine extraction, completion, and quality control mechanisms, alongside robust methods for managing uncertainty and ensuring the continuous evolution of KGs in dynamic environments. Comprehensive, dynamic quality assurance frameworks integrated throughout the KG lifecycle are needed to continuously monitor and adapt to evolving data uncertainty and source reliability [55]. Advancements in semantic parsing for grounding natural language to logical forms also hold promise for enriching KG utility [72].
6.2.2 Ontology Evolution
The dynamic and adaptive nature of knowledge in real-world applications necessitates robust mechanisms for ontology evolution. Ontology evolution refers to the incremental process of updating, refining, and extending an ontological knowledge base to accommodate new information, adapt to changing domains, and resolve inconsistencies [3]. Traditionally, this process has been resource-intensive, requiring significant manual effort and domain expert involvement for tasks such as initial ontology creation, cleaning, enrichment, and schema matching [3,6,48]. The manual or crowdsourced nature of ontology development and curation has historically presented significant scalability and automation challenges, highlighting the need for more autonomous approaches [3].
The advent of Large Language Models (LLMs) has opened new avenues for automating ontology evolution. LLMs possess strong capabilities in concept recognition, abstraction, and pattern identification, which are foundational for tasks such as automated construction of conceptual hierarchies, ontological category expansion, attribute completion, ontology alignment, and concept normalization [12]. This potential suggests that LLMs can dynamically maintain and evolve ontologies by monitoring new information and trends, then proposing updates to the knowledge base [52]. However, integrating new information into ontological structures and dynamically updating relationships remains a complex challenge [7].
Ontology Evolution Approaches
| Approach / Strategy | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Manual / Human-Driven | Experts manually update, refine, and extend ontologies. | Ensures high precision, contextual understanding. | Initial ontology creation, cleaning, schema matching. | Resource-intensive, time-consuming, scalability bottleneck, human bias. |
| LLM-Driven Autonomous Evolution | LLMs propose & validate ontology edits, generate justifications. | Automates update/maintenance, adapts to changing domains. | Evo-DKD (dual knowledge decoding, Validation Module, Justification Cross-Check). | Hallucination risk, ensuring formal structural integrity, consistency with existing KG. |
| Community-Driven / Iterative | Collaborative, open-source model with continuous updates. | Facilitates broad contributions, ensures long-term adaptability. | KNOW ontology (GitHub-managed, open-source). | Managing diverse contributions, ensuring quality/consistency. |
| Continuous Learning Systems | Systems continuously extract, refine, and improve KBs. | Dynamic adaptation, self-improvement, removes outdated information. | NELL (Never-Ending Language Learner), rule-based forgetting/consolidation systems. | Requires robust validation, computational cost, potential for inconsistencies. |
| Concept Recognition & Abstraction | LLMs identify concepts, build hierarchies, expand categories. | Supports automated schema development, attribute completion. | LLM capabilities for concept normalization, ontological alignment. | Reliability of LLM-generated concepts, ensuring semantic integrity. |
A significant technical innovation in LLM-driven autonomous ontology evolution is the “dual knowledge decoding” mechanism introduced by Evo-DKD [17]. This framework operates on the underlying assumption that effective ontology evolution requires a combination of formal structural integrity and contextual grounding. Evo-DKD employs a dual-decoder architecture where LLMs generate both structured ontology edits and corresponding natural language justifications. This architecture allows the system to identify new information by processing user queries, the current ontology state, and relevant textual contexts, which are then translated into candidate ontology edits. To ensure consistency and accuracy, Evo-DKD incorporates a Validation Module that performs Ontology Consistency and Constraints checks against schema-level rules, preventing duplication and redundancy. Furthermore, a Justification Cross-Check mechanism verifies the factual support of the structured claims against their natural language explanations. Validated edits are then injected into the knowledge base, forming a closed-loop autonomous updating system that informs future reasoning. This approach addresses challenges in automated knowledge base maintenance by ensuring proposed changes are both formally correct and contextually grounded. Experimental results demonstrate Evo-DKD’s superior performance, with its Full Dual-Decoder mode consistently outperforming single-mode baselines in terms of precision of ontology updates and downstream task performance, achieving Relaxed Match Accuracy over 0.7 in healthcare and significant gains in cultural heritage timeline modeling. The BERTScore for explanations also confirmed the superior semantic coherence of the dual-decoder mode [17].
The effective integration of structured, domain-specific knowledge is crucial for enhancing LLMs’ understanding and generation capabilities. Frameworks like KNOW [36] exemplify how explicit ontologies can serve as dynamic assets rather than static resources. KNOW, conceptualized as an evolving commonsense ontology, adopts an iterative, collaborative, and open-source development model managed through platforms like GitHub. This architectural choice facilitates continuous updates and extensions, driven by community contributions and real-world use cases, ensuring the ontology’s adaptability and relevance over time. By providing a structured framework, KNOW directly guides the identification of new information and the incorporation of changes, which are fundamental to practical ontology evolution. This contrasts with systems like StructSense, which utilize curated ontologies for semantic grounding but primarily treat them as static resources, focusing on the use of existing knowledge rather than its autonomous evolution [70]. Similarly, approaches that leverage existing ontological structures, such as WordNet and Wikidata, to derive “cleaner and more abstract” conceptual knowledge for LLMs demonstrate the benefit of structured knowledge but do not detail mechanisms for their dynamic evolution [7]. These methods highlight a “Knowledge Complexity Mismatch,” where LLMs benefit from pre-structured and abstracted knowledge, reinforcing the need for continuously evolving ontologies.
Addressing the challenges of consistency, accuracy, and scalability in automated knowledge base maintenance is paramount. While Evo-DKD provides a direct solution for consistency and accuracy through its validation modules, the hallucination problem inherent in LLMs remains a significant concern, potentially introducing inconsistencies or incorrect information into autonomously evolved ontologies [12]. The need for methods to reconcile LLM-driven evolution with human expertise to ensure semantic integrity is thus critical. Beyond direct validation, other works contribute to maintaining knowledge base quality. For instance, the forgetting_and_consolidation_for_incremental_and_cumulative_knowledge_acquisition_systems framework proposes a dynamic rule set evolution system that acquires, evaluates, and manages rules based on quality and consistency metrics, thereby ensuring the knowledge base remains relevant and free from useless or inconsistent rules. While not explicitly focused on formal ontologies, its principles of dynamic maintenance are applicable. For factual accuracy, KnowMap dynamically updates facts, ensuring that newly acquired information supersedes existing ones to reflect the current state, though its scope is primarily instance-level rather than schema evolution [44]. Scalability, a persistent challenge in manual ontology development, is addressed by continuous learning approaches such as those proposed for knowledge_graph_extension_by_entity_type_recognition, which conceptualize KG evolution as continuous enhancement through streaming data and updated machine learning models, laying the groundwork for more autonomous processes via platforms like LiveSchema.
Despite these advancements, several limitations and areas for future research persist. Many existing frameworks either outline ontology evolution as a future direction or focus on initial construction and static knowledge encoding, rather than providing explicit mechanisms for autonomous schema-level changes [5,11,20,30,71,74]. The nuanced challenge of integrating new information into existing ontological structures and dynamically updating their relationships, particularly with explicit semantic consistency, remains largely unaddressed in many studies [7]. Moreover, while the problem of representing uncertainty at the ontology level has been explored through OWL extensions like Fuzzy-OWL and OntoBayes, a comprehensive framework for autonomous ontology evolution that dynamically adapts its structure and rules in response to “knowledge deltas” and evolving uncertainty profiles is still an open question [55]. Future work must also focus on bridging theoretical models of symbolic evolution, such as those emphasizing socially bootstrapped code and delta convergence in semantic space, to practical computational implementations that ensure dynamic updates and semantic consistency [46]. Furthermore, detailed technical mechanisms for managing versioning, tracking changes, and implementing safeguards against biased information during autonomous evolution are essential for robust ontology management [58].
6.3 Model Extraction and Cybersecurity
The intersection of model extraction and cybersecurity represents a critical frontier in modern artificial intelligence, encompassing both offensive capabilities to compromise machine learning systems and defensive measures to secure them. This domain involves complex challenges related to intellectual property, data privacy, and the integrity of AI-driven services.
Model Extraction and Cybersecurity Applications
| Application Type | Core Goal | Key Mechanisms / Approaches | KAB Addressed / Benefit | Limitations / Challenges |
|---|---|---|---|---|
| Offensive: MLaaS Model Extraction | Replicate proprietary ML model from black-box oracle. | Query-based active learning (Uncertainty, K-center, Adversarial), Universal Thief Datasets. | Efficient replication of model functionality under budget constraints. | IP infringement, privacy risks, limited to classification, assumptions about query access. |
| DNN Extraction | Replicate Deep Neural Networks. | Active learning + diverse public datasets (ImageNet, WikiText-2). | High agreement scores (e.g., 4.70x image, 2.11x text improvement over baselines). | Primarily focuses on classification, not complex generative models. |
| GNN Extraction | Replicate Graph Neural Networks. | Active sampling (representativeness, uncertainty, diversity) for graph structures. | Cost-effective GNN model acquisition under limited query budgets. | Specialized for graphs, may not fully generalize. |
| Defensive: LLM/MLaaS Security | Safeguard AI systems from unauthorized access/misuse. | Secure deployment strategies, internal LLM security mechanisms. | Protects IP, sensitive data, prevents misuse (jailbreaks). | Requires continuous adaptation against evolving threats, balancing security/usability. |
| Secure LLM Deployment | Protecting sensitive data and operations. | On-premises LLMs, Secure RAG, Sandboxing, Data Anonymization, Encryption. | Mitigates data exfiltration, ensures data privacy. | Computational costs, complexity of implementation. |
| LLM Internal Security | Preventing malicious use & undesirable behavior. | Architectural design (modularity), Machine Unlearning, Knowledge Editing. | Reduces “jailbreak” success, prevents toxic content generation. | Efficacy of unlearning, side effects of editing, internal mechanism opacity. |
| Defensive: Binary Code Analysis | Identify vulnerable code, detect IP infringement. | Learning invariant semantic representations across compilation environments. | Pluvio (MPNet, RL Removal module, CVIB) for OOD clone search. | High computational cost, requires specialized expertise, focuses on code. |
One primary aspect of offensive cybersecurity is the extraction of proprietary machine learning models from Machine Learning as a Service (MLaaS) platforms. The framework presented in [15] directly addresses this by demonstrating how Deep Neural Networks (DNNs) can be replicated for image and text classification tasks with limited query budgets. The underlying assumption is that an attacker has black-box access to the MLaaS model, and the theoretical foundation leverages active learning to optimize query selection. Architectural choices include the use of universal thief datasets (e.g., ImageNet subsets, WikiText-2) to provide diverse, domain-agnostic inputs for querying, combined with various active learning strategies such as Uncertainty, K-center, Adversarial (DFAL), and an ensemble Adversarial+K-center approach. This framework achieved substantial performance gains, with an average of 4.70x improvement in agreement scores for image tasks and 2.11x for text tasks over uniform noise baselines with a 30K query budget. For instance, on CIFAR-10, the Adv+K-center strategy reached 78.36% agreement, significantly surpassing the 10.62% of uniform noise, albeit with 100K queries [15]. The implications are profound, exposing MLaaS providers to significant privacy vulnerabilities and intellectual property infringement, as extracted models can be used for adversarial attacks, model inversion, or unauthorized use without incurring query costs [15].
Extending model extraction to specialized architectures, CEGA (Cost-Effective Graph-based Model Extraction and Acquisition) focuses on GNN Model Extraction With Limited Budgets for node classification tasks [45]. CEGA’s theoretical foundation and architectural design are specifically tailored to the graph domain, aiming to replicate GNN functionality while adhering to stringent query budget constraints (overall budget $B$ and per-cycle $\kappa$). The method mitigates security risks like copyright violations, patent infringement, unauthorized redistribution, and unfair competition stemming from Model Extraction Attacks (MEAs) by assessing the vulnerability of GNNs. CEGA is evaluated using accuracy, fidelity (behavioral similarity), and F1 score, demonstrating superiority over baselines like Random, GRAIN, and AGE across diverse graph datasets (e.g., Coauthor-CS, Amazon-Computer) under limited query budgets (e.g., $2C$ to $20C$ queried nodes) [45]. While both frameworks address model extraction from MLaaS platforms under budget constraints, [15] offers a more general approach for DNNs using universal datasets, whereas CEGA [45] is specialized for GNNs, highlighting the domain-specific adaptations necessary for different model architectures. Both approaches underscore the inherent Knowledge Acquisition Bottleneck (KAB) when attempting to replicate unknown models, overcoming it by strategic, optimized querying techniques.
Beyond model extraction, binary analysis presents a critical cybersecurity application, particularly in identifying vulnerable code and intellectual property infringements. Pluvio [24] addresses the challenge of assembly clone search, focusing on “out-of-domain architectures and libraries.” The solution’s core assumption is that assembly code, despite its low-level nature, contains semantic information that can be extracted and made invariant to compilation specifics. Pluvio overcomes the KAB for unseen architectures and compilers by learning invariant semantic representations through a combination of transfer learning and information bottleneck theory. Its architectural choices include:
- Pre-trained NLP Models (MPNet): Leveraging
all-mpnet-base-v2to treat assembly code as text, capturing broad “human common knowledge” about code semantics. - RL
RemovalModule: A reinforcement learning agent designed to prune noisy and redundant tokens arising from function inlining and compiler-injected code, effectively managing sequence length limitations inherent in assembly code. - Conditional Variational Information Bottleneck (CVIB): This novel learning strategy is crucial for “forgetting” nuisance information related to architectures and optimization settings (L2). By doing so, CVIB enables the model to learn robust, disentangled embeddings that generalize effectively to unseen architectures and libraries.
Pluviosignificantly improves upon state-of-the-art baselines, achieving an 88.7% AUC and 82.5% accuracy in comprehensive out-of-domain scenarios (OOD-ARCH&LIBS), representing over a 35% improvement compared to existing methods likeOrder Matters[24]. This capability to detect code clones across diverse compilation environments is vital for proactive security and intellectual property protection.
On the defensive front, ensuring the trustworthiness and security of Large Language Models (LLMs) and Knowledge Extraction (KE) systems is paramount. The survey in [30] explores the underlying causes of security risks in LLMs, such as “jailbreak” attacks and the generation of toxic content. It assumes that certain internal parameters or “toxic regions” within LLMs are inherently linked to undesirable outputs. Strategies to address these issues include architectural design emphasizing modularity and sparsity, machine unlearning to forget privacy-sensitive or toxic information, knowledge editing to deactivate problematic neurons, and representation editing to manipulate hidden states for improved safety. While focused on internal LLM security, this work highlights the need for robust model design against misuse. Complementing this, [48] emphasizes the need for trusted applications in mission-critical industries, particularly regarding processing confidential data without exposure to third parties. This paper assumes that secure deployment strategies are essential to protect sensitive data and intellectual property in KE and LLM contexts. It advocates for defensive measures such as on-premises LLMs, Secure Retrieval Augmented Generation (RAG), sandboxing, data anonymization, PII scrubbing, differential privacy, access control, encryption, logging, and red-teaming strategies [48]. These strategies aim to prevent unauthorized model extraction, data exfiltration, and ensure the integrity of LLM operations. The focus here is on securing the deployment and interaction with LLMs, whereas [30] addresses the intrinsic security and behavior of the LLM itself.
Ethical and Legal Implications: A critical comparison arises between the ethical and legal implications of model extraction and the security benefits of clone search. Model extraction frameworks, as demonstrated by [15,45], explicitly raise concerns about intellectual property infringement, copyright violations, patent infringement, unauthorized redistribution, and privacy vulnerabilities for MLaaS providers. The risk of verbatim memorization by models also contributes significantly to copyright and legal challenges [60]. Conversely, clone search technologies like Pluvio [24] offer substantial security benefits by enabling the identification of vulnerable code snippets, detection of intellectual property infringements in distributed binaries, and proactive risk management in software supply chains. While both capabilities involve analyzing and understanding proprietary code or models, the former represents an adversarial act, while the latter serves a protective purpose, demonstrating a critical duality in machine learning applications for cybersecurity.
Limitations and Future Research: Despite significant advancements, several limitations and areas for future research persist. The current model extraction frameworks, such as those for general DNNs [15] and GNNs [45], primarily focus on supervised classification models. Their applicability to more complex MLaaS offerings, such as generative models (e.g., LLMs) or reinforcement learning agents, remains largely unexplored. Future work should investigate extraction techniques for these advanced model types and develop corresponding defense mechanisms. Similarly, while offensive techniques are well-demonstrated, the papers often only briefly touch upon robust defensive mechanisms, presenting an imbalance in the research landscape [15,45]. There is a need for more detailed analysis of the financial and legal ramifications of successful model extraction, as well as the development of specific, evaluated defenses against such attacks. For binary analysis, while Pluvio [24] excels at out-of-domain generalization, broader MLaaS security implications, such as privacy vulnerabilities beyond IP infringement, are not deeply explored. Future research could focus on expanding these techniques to identify more subtle forms of malicious behavior or novel attack surfaces in binaries. Furthermore, the defensive strategies for LLMs [30,48] provide a strong foundation but require continuous adaptation as LLM capabilities and attack vectors evolve. Bridging the gap between internal model safety (e.g., machine unlearning, knowledge editing) and external deployment security (e.g., sandboxing, differential privacy) offers a fertile ground for developing holistic trustworthy AI systems. Research into machine unlearning and privacy-preserving training methods, particularly for data that contributes to verbatim memorization, remains crucial for mitigating legal and ethical risks [60].
6.4 Robotics and Autonomous Systems
Robotics and autonomous systems represent a critical domain where the Knowledge Acquisition Bottleneck (KAB) poses significant challenges, particularly due to the inherent complexities, uncertainties, and dynamic nature of real-world physical environments. Learning-based approaches offer a powerful mechanism to acquire knowledge that is otherwise intractable or labor-intensive to hand-code, enabling robots to perform complex tasks with enhanced adaptability and robustness [64]. This section systematically presents how various learning paradigms address the KAB in robotics, focusing on distinct types of behavior, analyzing the underlying assumptions, architectural choices, and their impact on performance.
Learned Behaviors and Knowledge Acquisition in Robotics
| Behavior Category | Core Mechanisms / Goals | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Manipulation | Handling objects with varying properties, in-hand manipulation, deformable/divisible objects. | Overcomes intractable analytical modeling for complex dynamics, adapts to uncertainty. | Learned compliant trajectories, reactive policies, grasp prediction, 3D soft-body reasoning. | Scalability to high DOF, unmodeled dynamics, data scarcity for real-world scenarios. |
| Locomotion | Robust & efficient gaits, navigation, collision avoidance across terrains. | Generates dynamic movement, adapts to changing conditions & environments. | Learned gaits for multi-legged robots, dynamic balance, reactive behaviors from sensors. | “Reality gap” from simulation, sample inefficiency, need for large datasets. |
| Human-Robot Interaction (HRI) | Recognizing human intent, generating responsive motions, collaboration. | Enables robust human-robot collaboration, adaptive behavior. | Learning from demonstration (Imitation Learning), adaptive behaviors for hardware damage. | Safety risks, foreseeing human actions, transferring to real-world HRI. |
| RL for Exploration/Skill Acquisition | Acquires knowledge through active interaction with environment. | Efficient exploration, policy transfer, intrinsic motivation. | InfoBot (Information Bottleneck, intrinsic reward), IBOL (unsupervised skill discovery). | Sparse rewards, sample inefficiency, reward function design complexity. |
| Cognitive Robotics / World Models | Understanding physical environments, dynamics, relationships. | Forms comprehensive cognition of the world, essential for general AI. | Explicit ontologies, domain-independent planners, KnowMap (dynamic environmental/experiential KB). | Learning from perceptual interaction, abstracting concepts, integrating multimodal data. |
| Bridging Symbol-Subsymbolic | Links raw perceptual data to symbolic planning. | Human-interpretable plans, robust to noisy inputs. | Latplan (State/Action Autoencoders for PDDL generation). | “Symbol Stability Problem,” uniform sampling issues. |
Learning has been extensively applied to a wide array of robotic behaviors, categorized broadly into manipulation, locomotion, and human-robot interaction. In manipulation, learned solutions enable robots to handle objects with varying properties and in diverse scenarios, where traditional model-based control struggles with unmodeled dynamics and high degrees of freedom [64]. For fixed objects, robots learn compliant trajectories for tasks like flipping light switches or opening doors, often by learning unconstrained degrees of freedom when the kinematic chain is closed. Spatially constrained behaviors, such as peg-in-a-hole or wiping, benefit from learned reactive policies derived from visual or force sensors, allowing for precise control and adaptation to environmental contact [64]. Handling movable objects, including grasping, pick-and-place, and complex in-hand manipulation, leverages learning to predict grasp poses from sensory inputs and manage uncertainty in object locations. The extreme complexity of dealing with deformable objects (e.g., knot tying, handling garments) and divisible objects (e.g., cutting, peeling) is addressed by learning to reason about 3D soft bodies and induced dynamics, tasks that are exceedingly difficult to model analytically [64]. Furthermore, dynamic manipulation tasks like batting, throwing, and balancing (e.g., inverted pendulum) demonstrate the advantage of learned behaviors in achieving precise control and adapting to highly sensitive, perturbation-prone dynamics, often requiring advanced perception of future trajectories [64].
For locomotion, learning facilitates the generation of robust and efficient gaits for diverse robotic platforms, including six-legged, quadrupedal, and bipedal robots, across varied terrains (e.g., stairs, rough terrain) and dynamic conditions [64]. Learning algorithms enable robots to acquire skills such as jumping across gaps, standing up dynamically, and maintaining balance by modifying gaits or controlling motor torques. Navigation and collision avoidance for locomotion rely on learning reactive behaviors from visual inputs or laser scan data, enabling reliable movement through complex and dynamic environments while managing pose uncertainty [64]. Beyond basic movement, learning also supports higher-level locomotion behaviors like dribbling for soccer and active exploration to maximize map accuracy in Simultaneous Localization and Mapping (SLAM) [64].
Human-robot interaction (HRI) and other complex behaviors highlight the utility of learning in achieving robust collaboration and adaptability. Tasks such as handing over objects, assisting with dressing, or social interactions demand robots to recognize human intent and generate natural, responsive motions [64]. Learning also facilitates the sequencing of complex tasks (e.g., coffee preparation) and, notably, enables robots to adapt behaviors to unforeseen hardware damage, maintaining functionality despite physical changes [64].
Reinforcement Learning (RL) frameworks have emerged as a dominant paradigm in autonomous systems for effectively overcoming KABs related to sparse rewards, exploration in vast state spaces, and generalization across tasks. The InfoBot framework, for instance, leverages information-theoretic principles to learn “useful habits” (default policies) and identify “decision states” (critical junctions requiring goal-dependent actions) [56]. By operating on continuous control tasks, InfoBot demonstrates superior performance in sparse reward settings. In MiniGrid environments, it achieves significantly higher success rates (e.g., 81% on FindObjS7 vs. 56% for baseline A2C; 85% on MultiRoomN5S4 vs. 0% for count-based or VIME), showcasing improved generalization of learned behaviors. Similarly, in goal-based MiniPacMan, InfoBot attained a 64% success rate after training on smaller mazes, dramatically outperforming traditional RL methods like A2C (5%) and PPO (8%) [56]. The framework’s ability to use “high value states” as goal proxies contributes to its efficacy in continuous control MuJoCo tasks like Humanoid and Walker2D, where it consistently surpasses PPO and SAC baselines in task return [56].
Another critical RL development is the Information Bottleneck Option Learning (IBOL) framework, which addresses unsupervised skill discovery. IBOL’s architectural choice involves an options framework and uses SAC (for the linearizer) and VPG (for skill policies) to learn a diverse set of fundamental behaviors without explicit reward functions [35]. Its strength lies in efficiently exploring and providing useful primitives that reduce the effective horizon for downstream tasks, making it particularly effective for policy transfer. In MuJoCo environments (Ant, HalfCheetah, Hopper, Humanoid), IBOL discovers more diverse locomotion skills and varied behaviors compared to state-of-the-art methods like DIAYN-L and DADS-L. Quantitatively, IBOL outperforms these baselines on information-theoretic metrics such as $I(Z; S_T^{\text{(loc)}})$ and WSEPIN, demonstrating superior informativeness and disentanglement of learned skills [35]. This leads to significantly improved performance and smaller variance in downstream tasks like AntGoal and CheetahImitation, by providing better abstractions for meta-controllers [35]. Both InfoBot and IBOL leverage information bottleneck principles, but InfoBot focuses on learning generalizable navigation and decision-making strategies through “useful habits” and “decision states,” while IBOL specializes in discovering and disentangling fundamental, diverse motor skills. Their shared theoretical foundation allows for robust knowledge compression, enabling efficient transfer and exploration. The theoretical work on recursive bootstrapping for information bottleneck, as illustrated by grid world navigation, further underpins the computational efficiency of acquiring relevant knowledge by avoiding high-dimensional state space searches and bootstrapping through low-dimensional latents [46].
Beyond learned behaviors, the development of robust autonomous systems necessitates foundational knowledge and cognitive capabilities. The concept of “world models,” which encompass a comprehensive understanding of physical environments, their dynamics, and complex relationships, is crucial for general AI and robust autonomy [12]. These models must integrate multimodal data across temporal and spatial dimensions to form a true cognition of the world, including commonsense knowledge essential for physical interaction [12]. While traditional Knowledge Representation (KR) in cognitive robotics utilizes explicit ontologies, domain-independent planners (e.g., PDDL), and belief management systems (e.g., Dynamic Epistemic Logic) for higher-level reasoning, planning, and ethical considerations [29], a major challenge remains in learning this world knowledge directly from perceptual interaction and autonomously abstracting concepts for decision-making [12,30]. Approaches like Latplan conceptually bridge symbolic planning with deep latent spaces, suggesting future avenues for integrating high-level action sequences with low-level actuation for physical robotics [28]. Contemporary efforts, such as KnowMap, explore knowledge-driven task adaptation for LLMs in embodied AI within text simulation environments, highlighting the potential for dynamic environmental and experiential knowledge to enhance adaptation and reasoning [44]. Similarly, frameworks aiming for metacognition in cognitive robotic applications emphasize lifelong learning of ontological concepts and interaction within human-AI teams, albeit currently in simulated settings [58].
Despite significant advancements, several limitations and challenges impede the widespread deployment of these systems outside controlled environments. A pervasive issue is the scalability and versatility of learned skills; many are task-specific, limited in their generalization across minor variations, and often require extensive retraining [64]. The sim-to-real gap remains a formidable barrier, as methods demonstrating strong performance in simulated environments (e.g., MuJoCo for IBOL [35], MiniGrid for InfoBot [56], text simulations for KnowMap [44]) often struggle with direct transfer to physical robots due to unmodeled dynamics, sensory noise, and complex hardware interactions. Specifically, applying methods to environments with very high-dimensional state spaces, like vision environments, where learned signals may not be directly feasible, presents an ongoing challenge for unsupervised skill discovery [35].
Furthermore, critical aspects such as robustness and safety are frequently under-addressed in skill learning literature [35]. The reliance on text corpora for current LLMs, leading to issues like hallucination and elementary commonsense reasoning, presents significant robustness deficiencies for building reliable world models for physical interaction [12]. The methodological flaw of repeatedly tackling simple problems with new algorithms, rather than addressing broader, more complex scenarios, limits the overall progress in the field [64]. Indeed, for highly structured and real-time multi-agent scenarios such as robotic soccer, hand-crafted behaviors still often outperform learned counterparts [64]. Future research must focus on practical implementations of theoretical insights, such as integrating symbolic action models with real-time sensor data and control loops [28], and developing architectures that enable AI systems to acquire knowledge directly from physical interaction, autonomously abstract concepts, and guide decision-making in complex and dynamic real-world environments [12,30,46].
6.5 Game Playing and Interpretable Reinforcement Learning
The realm of game playing has historically served as a critical benchmark for Artificial Intelligence (AI) advancements, pushing the boundaries of machine learning capabilities and, more recently, catalyzing the development of interpretable reinforcement learning (RL) frameworks. A primary objective within this domain is to address the knowledge acquisition bottleneck by enabling AI agents to not only achieve superhuman performance but also to articulate their learned strategies in a human-understandable manner, thereby bridging the “human-AI knowledge gap” [54].
Self-taught agents, most notably AlphaZero (AZ), exemplify this advancement by learning complex games like chess through self-play, surpassing human expertise without pre-programmed domain knowledge [54].
Game Playing and Interpretable Reinforcement Learning
| Approach / Framework | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| AlphaZero (AZ) Concept Discovery | Extracts “machine-unique concepts” (M-H knowledge) from latent space. | Bridges human-AI knowledge gap, provides novel strategic insights. | Convex optimization (sparse concept vectors), MCTS statistics, teachability/novelty metrics. | Human cognitive biases, differing computational capacities, small sample size for human studies. |
| Human-AI Knowledge Gap Bridging | Transferring AI-discovered concepts to human experts. | Expands human understanding, improves human performance. | Human studies with grandmasters, concept prototypes/puzzles. | Not merely knowledge transfer, managing cognitive/objective differences. |
| Interpretable RL (Robotics context) | Policies acquired lead to emergent, observable behaviors. | Implicit interpretability in dynamic tasks. | Imitation Learning, Policy Search (e.g., batting, pancake flipping). | Lack of full transparency, “reward hacking,” limitations in explicit interpretability. |
| InfoBot (Game Exploration) | Learning “useful habits” and “decision states” for exploration. | Tackles sparse rewards, improves policy generalization. | Information Bottleneck, KL divergence as intrinsic reward (MiniGrid, Atari). | Designing effective reward functions, variational approximations. |
| Latplan (Classical Planning) | Acquires symbolic PDDL models from unlabeled image pairs. | Provides transparency into AI reasoning, less data-intensive. | State Autoencoder, Action Autoencoder. | “Symbol Stability Problem,” uniform sampling, feature imbalance. |
| Unsupervised Skill Discovery | Learning interpretable & disentangled latent behavior representations. | Aids in making AI’s internal knowledge more understandable. | IBOL framework. | Primarily focuses on robotic control, not explicit game scenarios. |
A significant contribution in this area is the development of frameworks designed to extract “machine-unique concepts” (termed $M-H$ knowledge) from such agents [54]. These $M-H$ concepts represent novel units of knowledge not typically found in traditional human domain theory. In chess, for instance, AZ has revealed strategic queen sacrifices, unconventional pawn advances (e.g., b4 with an exposed king), and a prioritization of spatial control and piece activity that often outweighs immediate material gains or king safety, diverging from conventional human wisdom [54].
The methodology for discovering these concepts involves excavating insights from AZ’s latent policy-value network and Monte Carlo Tree Search (MCTS) statistics using convex optimization techniques [54]. Subsequent validation ensures the utility and novelty of these concepts. This process includes filtering for “teachability” (assessed by a student AI’s ability to learn the concept) and “novelty” (determined via spectral analysis comparing AI concepts against human game data) [54]. Once validated, these concepts are transferred to human experts, often through human-in-the-loop studies involving concept prototypes or puzzles. In a seminal study, four top chess grandmasters, including former World Champions, demonstrated significant accuracy improvements (ranging from +6% to +42%) in concept prototype positions after being exposed to AZ’s solutions, indicating an expansion of their own strategic understanding and representational space [54]. Qualitative feedback from these experts highlighted the AI-discovered concepts as “clever,” “very interesting,” and “something new,” confirming their practical implications for advancing human understanding and performance [54].
Despite these successes, bridging the human-AI knowledge gap presents significant challenges rooted in fundamental differences between human and AI reasoning. Human cognitive biases, such as “overthinking” or adherence to pre-existing strategies, can impede the adoption of AI-generated insights, even when proven effective [54]. Furthermore, AI agents often optimize for different objective functions (e.g., pure win probability) and operate under vastly different computational capacities compared to humans, whose practical play might prioritize robustness or simpler lines of attack over optimal but complex solutions [54]. This contrasts with symbolic rule learning approaches, as seen in [67], where a chess rule learning domain is used to illustrate incremental knowledge acquisition. While symbolic rules are inherently human-interpretable and facilitate consolidation, they typically do not yield the emergent, super-human insights characteristic of deep RL agents like AlphaZero [67].
Beyond high-strategy board games, interpretable RL extends to diverse game-playing contexts. In robotics, behavior learning applications demonstrate how policies acquired through imitation learning and policy search can lead to emergent behaviors in dynamic tasks such as batting, throwing, ball-in-a-cup, or pancake flipping [64]. For example, a robot learning to flip pancakes might discover a compliant vertical movement that implicitly reduces bouncing, offering an implicit form of interpretability in the emergent properties of the learned policy [64]. However, a lack of full transparency and the potential for “reward hacking” underscore the limitations in the explicit interpretability of these learned behaviors [64]. These robotic applications also face technical limitations, as perception and state estimation are often not learned end-to-end, and the “reality gap” between simulation and real-world performance often constrains the sophistication of learned behaviors [64].
Alternative approaches contribute to interpretability in different types of game-like environments. The InfoBot framework, for instance, tackles sparse rewards and exploration challenges in games like MiniGrid, MiniPacMan, and Atari by learning “default policies” and identifying “decision states” through an information bottleneck [56]. These “decision states” provide a form of interpretability by highlighting crucial junctures where an agent’s action becomes goal-dependent, drawing a conceptual link to “automatic vs. controlled action selection” in human cognition [56]. InfoBot has demonstrated superior policy generalization and exploration capabilities, even enabling cross-game transfer of learned encoders to accelerate learning in new environments [56].
For classical planning problems resembling games, such as the 8-puzzle or LightsOut, Latplan offers an approach that acquires symbolic PDDL (Planning Domain Definition Language) models directly from unlabeled image pairs representing game states and transitions [28]. This method contrasts with deep RL by requiring less data and providing theoretical completeness and optimality guarantees for the learned symbolic model [28]. Its output, including human-comprehensible visual plan executions and a symbolic PDDL model, provides transparency into the AI’s reasoning not typically found in black-box RL policies [28]. While not directly focused on AlphaZero-style concept discovery, its symbolic representation offers inherent interpretability that could potentially inform or constrain RL agents. Furthermore, research on unsupervised skill discovery, such as that by [35], aims to learn interpretable and disentangled latent representations of behaviors, which aligns with the broader goal of making AI’s internal knowledge more understandable, even if it primarily focuses on robotic control tasks rather than explicit game playing scenarios.
Critically, the generalizability of $M-H$ concept transfer remains an area for further research. The human studies validating AZ’s concepts, while impactful, involved a small sample size of grandmasters, limiting the statistical generalizability of the results [54]. Methodological flaws in prototype generation, which can yield “non-instructive puzzles,” also suggest areas for improvement in the transfer mechanism [54]. Future work should investigate how these transfer frameworks adapt to complex games with less defined concepts or non-deterministic elements, and explore optimal “human learning conditions” for concept assimilation [54]. The long-term impacts of learning AI concepts on human cognitive processes and creativity also present compelling unaddressed questions [54]. The scope of “game playing” also varies significantly; while high-strategy games like chess reveal profound strategic insights, robotic game tasks face challenges in end-to-end learning for perception and state estimation [64], and knowledge-driven LLM applications in open-world text-based games, like ScienceWorld [44], primarily focus on gathering information and accumulating experience rather than generating novel strategic concepts in a competitive setting. Similarly, interactive knowledge acquisition games like Twenty Questions, while demonstrating adaptive elicitation of latent information, do not engage with the interpretive challenges of high-performance RL agents [13]. A significant future direction lies in bridging symbolic and sub-symbolic AI paradigms: exploring how interpretable symbolic models or rule-based systems could inform or constrain deep RL agents, or conversely, how emergent, high-performing behaviors from deep RL could be formalized into human-understandable, transferable knowledge representations.
6.6 Educational Technologies, Knowledge Tracing, and Student Modeling
The effective alleviation of the Knowledge Acquisition Bottleneck (KAB) in educational contexts hinges on the development of sophisticated frameworks for knowledge tracing (KT) and student modeling. These frameworks aim to provide interpretable, actionable insights into students’ learning processes, facilitating personalized learning and assessment. While traditional KT methods often prioritize predictive accuracy, recent advancements, particularly those leveraging large language models (LLMs), have emphasized the critical need for human-understandable representations of student knowledge states [50].
Educational AI Applications for Knowledge Acquisition
| Application / Framework | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Language Bottleneck Models (LBMs) | LLM encoder-decoder generates natural-language knowledge summaries. | Interpretable knowledge tracing, actionable insights for educators. | GRPO for encoder optimization, human steerability. | Assumes “quasi-static knowledge states,” high computational cost, context length limits. |
| Multi-View Knowledge Model (MVKM) | Multi-view tensor factorization of student interaction data. | Models dynamic knowledge acquisition from diverse learning resources (learning & forgetting). | Shared student/temporal features, type-specific material concept matrices. | Lacks explicit human-in-the-loop mechanisms. |
| Adaptive Student Assessment | Meta-learned LLM strategically selects questions. | Efficiently maps student skill profile, identifies rare latent traits. | Maximizes information gain, maintains calibrated uncertainty. | Primarily focuses on question selection, not interpretable summaries. |
| Knowledge Graphs (KGs) in Education | Structuring learning content, recommending learning paths. | Personalized learning, improved learning efficiency. | Entity-level & schema-level knowledge for path generation. | Application often broad, lacks specific mechanisms for interpretable student states. |
| LLM-inspired AI for Learning | LLMs as learners (Self-Tuning), or for pedagogical concepts. | Improves LLM knowledge acquisition, self-reflection. | Self-Tuning framework (Feynman Technique inspired). | LLM is the learner, not the tool for human student modeling directly. |
| Metacognitive Abilities | Adaptive dialogue based on user traits & knowledge. | Enhances human-virtual patient interaction. | Maryland Virtual Patient (MVP). | Lacks specific technical details on knowledge tracing or empirical validation. |
A significant development in addressing the KAB through interpretable insights is the Language Bottleneck Models (LBMs) framework [50]. LBMs directly tackle the problem of opaque, uninterpretable student knowledge states inherent in many existing KT methods. Their architectural foundation lies in an encoder-decoder LLM structure, where an encoder LLM processes student interaction histories to generate concise, natural-language summaries of implicit knowledge states. A frozen decoder LLM then utilizes only this summary to reconstruct and predict student responses. The encoder is optimized using Group Relative Policy Optimization (GRPO), rewarding downstream decoding accuracy to ensure the generated summary is both predictive and semantically meaningful to humans [50]. This approach allows LBMs to identify mastered skills, unmastered skills, and specific misconceptions, capturing “deeper patterns reflecting conceptual mastery or specific misunderstandings” [50]. In comparative analyses, LBMs demonstrate predictive accuracy rivaling state-of-the-art KT models and direct LLM methods on benchmarks like the Eedi dataset, with instances where LBMs perform within 2% of direct prompting accuracy despite the information bottleneck [50]. A key advantage is their data efficiency, requiring orders of magnitude fewer student trajectories than traditional KT methods such as DKT, DKVMN, SAKT, or AKT to achieve comparable predictive power [50]. Furthermore, the natural-language bottleneck fundamentally enhances interpretability, providing information readily accessible for human understanding. The framework also supports human steerability through prompt engineering, reward signals, and direct augmentation of summaries by educators, which is crucial for personalized learning outcomes [50]. However, a primary limitation of LBMs is their underlying assumption of “quasi-static knowledge states,” which simplifies the dynamic nature of human learning and continuous knowledge evolution. Practical challenges include high computational costs and context length restrictions inherent to LLMs [50].
In contrast to LBMs’ focus on interpretable snapshots, the Multi-View Knowledge Model (MVKM) offers an approach to model dynamic knowledge acquisition from diverse learning resources [22]. MVKM addresses the problem of accurately tracking students’ evolving knowledge states as they engage with various learning materials (e.g., quizzes, videos, discussions) and elucidating the unique contributions of each material type. Architecturally, MVKM employs a multi-view tensor factorization, decomposing student interaction data across multiple material types into a shared student latent feature matrix ($S$), a shared temporal dynamic knowledge tensor ($\mathbf{T}$), and type-specific material concept matrices ($Q^r$). Critically, it integrates a flexible knowledge increase objective with a rank-based constraint to realistically model gradual learning and occasional forgetting, directly addressing the dynamic aspect of knowledge acquisition that LBMs simplify [22]. MVKM significantly outperforms conventional student knowledge modeling baselines (e.g., IBKT, DKT) in predictive accuracy (e.g., RMSE of 0.0613 and MAE of 0.0362 on the Canvas_H dataset) and provides interpretable insights into knowledge growth patterns and material difficulties [22]. The necessity of its rank-based learning and forgetting constraint highlights a fundamental difference from models assuming static knowledge, as without it, knowledge trends become “elusive and counter-intuitive” [22].
Beyond explicit KT models, LLMs are being leveraged for adaptive student assessment. A framework utilizing a meta-learned LLM strategically selects questions to maximize information gain about a student’s skill profile, efficiently mapping their “knowledge boundaries” and “underlying skills” [13]. This method is particularly effective for identifying “rare latent traits,” achieving over 10x higher percent gain over random for hard questions. While highly effective in optimizing question selection and maintaining calibrated uncertainty, this approach does not primarily focus on generating human-interpretable natural-language summaries of student knowledge states, distinguishing it from LBMs [13].
Knowledge Graphs (KGs) also play a role in educational technologies by structuring learning content and recommending learning paths. A knowledge graph-based system, for instance, utilizes entity-level and schema-level knowledge to generate personalized learning paths from fragmented content, aiming to improve learning efficiency and content depth [31]. While KGs offer a structured way to represent educational content and facilitate e-learning systems, their application often remains broad, as noted by surveys identifying “Education” as a domain for KGs without detailing specific mechanisms for interpretable student knowledge states or addressing KAB directly [74]. This contrasts with the targeted interpretability and diagnostic capabilities of LBMs and MVKM.
Some works draw inspiration from human learning processes or use pedagogical concepts metaphorically for AI development, rather than directly contributing to human student modeling. For example, some research draws an analogy between LLMs prioritizing QA performance over deep understanding and human “study for the test” behavior, underscoring the challenge of achieving truly comprehensive student models if only task performance is measured [73]. Similarly, the “Self-Tuning” framework for LLMs is inspired by the Feynman Technique, applying pedagogical concepts like “memorization, comprehension, and self-reflection” to improve an LLM’s knowledge acquisition, but the LLM itself is the learner, not the tool for human student modeling [68]. Other research explores metacognitive abilities in virtual patient systems, like the Maryland Virtual Patient (MVP) for medical students, demonstrating adaptive dialogue based on user traits and knowledge. However, this work often lacks specific technical details on knowledge tracing algorithms or empirical validation of student learning outcomes [58]. These examples illustrate how educational principles inform AI design but do not directly address the core challenge of interpreting and modeling human knowledge states for personalized instruction.
In synthesizing these approaches, a critical insight emerges: the field is transitioning from purely predictive black-box models to more transparent, interpretable systems that actively address the KAB. LBMs represent a significant leap by generating human-readable summaries through LLM encoder-decoder architectures, offering unparalleled interpretability and human steerability. This enables personalized feedback and interventions by educators. However, the quasi-static knowledge states assumption of LBMs limits their applicability to dynamic learning, a challenge more explicitly handled by models like MVKM, which actively model learning and forgetting. Future research must focus on integrating the interpretability benefits of LLM-based approaches with robust modeling of dynamic knowledge acquisition, overcoming computational and context length limitations of current LLMs. Quantitatively comparing the interpretability of these models against human expert assessments remains an unaddressed question for LBMs. Ultimately, advancing these methods will contribute to more effective, personalized learning and assessment systems that provide genuinely actionable insights into student knowledge and progress.
6.7 Other Domain-Specific Applications
The practical utility of frameworks and algorithms designed to mitigate the Knowledge Acquisition Bottleneck (KAB) extends across a diverse array of specialized domains, moving beyond general natural language processing or computer vision tasks. These applications demonstrate how tailored approaches, grounded in specific theoretical foundations and architectural choices, offer effective solutions for unique domain challenges, ranging from automated event detection in healthcare to complex predictive modeling in industrial settings and socio-economic analysis.
Domain-Specific Applications: Healthcare and Socio-economic
| Domain / Application | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Clinical & Healthcare: Event Detection | Deep learning for automated detection from EHRs. | Overcomes manual chart review, handles rare events. | CNN, LSTM, Bi-LSTM, TCN for hypoglycemia detection. | Interpreting numerical values, data scarcity, flexible clinical language. |
| Clinical & Healthcare: Predictive Modeling | LLMs for expert prior elicitation. | Reduces labeling effort, improves predictive accuracy in data-scarce settings. | AutoElicit (UTI prediction). | Bias propagation from LLM-elicited priors, lack of explicit validation. |
| Clinical & Healthcare: KG Construction | Integrating biomedical sources into KGs. | Improves clinical decision support, drug repurposing. | CovidGraph, DRKG, HKGB (human-in-the-loop validation). | Manual annotation, error-prone IE, LLM limitations, ethical concerns (reproducibility). |
| Clinical & Healthcare: Biomedical Text Mining | Automating IE for scientific literature. | Accelerates knowledge transfer, structures vast literature. | KeBioLM (knowledge injection), Confidence-based re-annotation, KRDL, SciBERT. | Knowledge Complexity Mismatch, Ineffective Utilization, data quality issues. |
| Socio-economic & Environmental: Poverty Mapping | ML/DL models extract knowledge from satellite imagery. | Augments traditional surveys, enables high-resolution mapping. | SVM, Random Forests, XGBoost, CNNs (ResNet, Inception-Net) + NTL/DHS data. | Lack of scientific insight/interpretability (“why”), static models, generalizability issues. |
| Knowledge-based Visual Question Answering (KVQA) | Multimodal reasoning + external world knowledge. | Answers questions beyond image content, disentangles knowledge acquisition. | DKA (LLM for decomposition, PromptCAP for captioning, ChatGPT for retrieval). | Insufficient caption model, susceptibility to multimodal hallucinations. |
The clinical and healthcare domain represents a significant area where overcoming the KAB is critical due to the vast, complex, and often sensitive nature of medical data. Deep learning approaches have been particularly effective in tasks such as automated event detection from Electronic Health Records (EHRs). For instance, a high-performing NLP system employing Convolutional Neural Networks (CNN), Long Short-Term Memory (LSTM), Bidirectional LSTM (Bi-LSTM), and Temporal Convolutional Networks (TCN) was developed for automatically detecting hypoglycemia events from unstructured clinical notes [21]. These models, initialized with 100-dimension Word2Vec embeddings trained on combined public and medical corpora, achieved high performance (e.g., F1=$0.91 \pm 0.02$, ROC-AUC=$0.998$) in a 10-fold cross-validation. This addresses the challenge of manually reviewing patient charts and the limitations of ICD codes, despite difficulties with flexible clinical language and rare event data scarcity. A notable limitation was the model’s struggle to interpret numerical blood sugar values without explicit external human knowledge, highlighting an interpretability challenge [21].
Beyond event detection, knowledge acquisition plays a crucial role in predictive modeling and decision support. The AutoElicit framework applies Large Language Models (LLMs) for expert prior elicitation in predictive modeling, particularly in healthcare where labeled data is scarce [19]. It demonstrated significant accuracy improvements in predicting Urinary Tract Infections (UTIs) in dementia care from sensor recordings, saving over six months of labeling effort by achieving performant accuracy 220 days earlier with only 15 labels. This framework emphasizes interpretability and robustness by producing priors for linear models, crucial for clinical acceptance. Similarly, Language Bottleneck Models (LBMs) are conceptualized for clinical decision support, aiming to distill patient data into auditable textual state descriptions that forecast outcomes [50]. The theoretical framework information_must_flow_recursive_bootstrapping_for_information_bottleneck_in_optimal_transport offers conceptual insights into neurobiological processes, such as Parkinson’s Disease and Alzheimer’s Disease, by modeling memory disruption as a breakdown of recursive inference cycles due to impaired structural integrity, though it lacks direct AI application and experimental validation in clinical outcomes [46].
Knowledge Graph (KG) construction and validation are also central to managing complex medical information. Frameworks like CovidGraph and DRKG (Drug Repurposing KG) integrate multiple biomedical sources (publications, genes, diseases, drugs) to improve clinical decision support and drug repurposing, with CovidGraph managing 36M entities and 59M relations [3]. The HKGB (Health Knowledge Graph Builder) semi-automatically constructs clinical KGs from Electronic Medical Records (EMR) with human-in-the-loop validation, highlighting the need for extensive human intervention for concept and relation mapping [3]. KGValidator was evaluated on the UMLS dataset, a medical ontology, to validate domain-specific triples, though it noted the challenge of sourcing pertinent external context for such complex domains [40]. Ontology evolution frameworks like Evo-DKD have also been applied to healthcare ontology refinement, dynamically updating knowledge graphs to improve downstream Retrieval-Augmented Generation (RAG) queries, for example, by adding triples about drug efficacy for weight management in diabetic patients [17]. However, uncertainty_management_in_the_construction_of_knowledge_graphs_a_survey highlights challenges like manual annotation effort, error-prone IE methods, and LLMs' poor performance on specific domains as limitations for clinical KGs. A comprehensive survey identified health as the most prominent domain for KGs in NLP, covering subdomains like biomedicine, pharmacology, and mental health, yet noted ethical concerns due to poor reproducibility metrics [74].
Biomedical text mining and Named Entity Recognition (NER) are critical for structuring vast scientific literature. Revisiting the Knowledge Injection Frameworks investigated biomedical NER using KeBioLM, a BioBERT-based model injecting entity knowledge from UMLS. Surprisingly, injecting aligned biomedical knowledge yielded comparable F1 scores to injecting random knowledge, indicating a Knowledge Complexity Mismatch and Ineffective Knowledge Utilization. This suggests that the challenge lies not merely in the availability of domain knowledge but in the model’s ability to effectively leverage it [7]. GPT-3-powered Information Extraction also tackled biomedical IE, but its in-context learning did not outperform fine-tuned BERT-sized models, suggesting limitations in addressing specialized domain accuracy and efficiency challenges [18]. Addressing data quality issues, single_versus_multiple_annotation_for_named_entity_recognition_of_mutations proposed confidence-based and similarity-based ranking methods to selectively re-annotate training data, significantly reducing the performance gap between models trained on single-annotated vs. double-annotated data for NER of genetic mutations from scientific literature. This method reduced the BioBERT F-score gap from 9.8% to 3.6% by re-annotating only 37.6% of the data, demonstrating a cost-effective strategy for high-quality data acquisition [25]. Deep learning for precision oncology also leverages knowledge-efficient deep learning (KRDL) for automating knowledge curation from biomedical literature [16]. The “Knowledge AI” framework applies fine-tuned models like SciBERT/BERT and BioGPT to medical (PubMedQA) and biological (GENIA) datasets for abstractive QA and NER, demonstrating strong domain understanding [2].
Advanced Retrieval-Augmented Generation (RAG) and KG approaches further enhance knowledge utilization. Graph-based Approaches and Functionalities in Retrieval Augmented Generation surveys specialized frameworks such as MedGraphRAG and HyKGE for healthcare, focusing on safety and dependability by iteratively refining answers with LLMs and leveraging KGs for reasoning chains [71]. REALM integrates RAG with multimodal EHRs to improve clinical predictive capabilities. For biomedical QA, GLBK uses KGs to retrieve and prioritize relevant documents from vast corpora like PubMed, mitigating biases and improving access to long-tail knowledge [71]. The Synthetic Knowledge Ingestion (Ski) method improves LLM performance in biomedical QA by addressing the domain knowledge deficit through knowledge refinement and injection [5]. StructSense, a task-agnostic agentic framework, applies schema-based extraction to clinical and psychological assessments in neuroscience, leveraging an ontology database for semantic grounding and improving data FAIRness [70]. The PU-ADKA framework enhances LLMs in drug discovery and cancer drug development by cost-efficiently acquiring specialized knowledge through expert interaction, utilizing Positive-Unlabeled learning for question-expert matching and Multi-Agent Reinforcement Learning for question selection, achieving significant improvements in win rates over baselines [4].
Limitations and Future Research in Clinical/Healthcare: A recurring challenge is the Knowledge Complexity Mismatch and Ineffective Knowledge Utilization where available domain knowledge (e.g., UMLS) is not effectively leveraged by models [7]. Data scarcity for rare medical events and the interpretability of numerical values remain critical issues [21]. Future research should focus on how to properly align semantic labels with medical ontologies to improve data integration and ontology management in clinical KGs [3]. Overcoming the ethical concerns of reproducibility identified in KG applications for health is also paramount [74]. Developing robust mechanisms for LLMs to effectively integrate and reason with complex biological concepts and graphical representations of chemical structures is a key direction [30]. The conceptual insights from frameworks like information_must_flow_recursive_bootstrapping_for_information_bottleneck_in_optimal_transport need to be translated into practical AI-driven diagnostic or therapeutic tools.
Robust knowledge extraction solutions are vital for industrial operations and business intelligence, where the accurate interpretation of domain-specific, often unstructured, data can significantly enhance safety, efficiency, and decision-making. In aviation, trusted_knowledge_extraction_for_operations_and_maintenance_intelligence focuses on extracting critical operational insights from unstructured FAA Accident/Incident reports. By evaluating 16 off-the-shelf NLP tools for NER, Coreference Resolution, Named Entity Linking, and Relation Extraction, the study highlighted significant performance limitations of general NLP tools and underscored the necessity for domain-specific adaptation to achieve reliable and trustworthy knowledge extraction in this specialized field [48]. This framework suggests transferability to other fields like healthcare, law, and logistics that share similar characteristics of specialized terminology and sensitive data.
In software development, nlp_based_relation_extraction_methods_in_requirements_engineering addresses the KAB in Requirements Engineering (RE) by automating the identification and classification of relations between textual requirements, using the European Rail Traffic Management System (ERTMS/ETCS) as a case study. Ontology-based methods (e.g., OpenReq-DD) offer interpretability and low computational costs, inferring relations like refines and requires with high efficiency (27 seconds for extraction). Machine Learning-based methods (e.g., fine-tuned BERT on the PURE dataset) provide expressive power, adaptability, and scalability, detecting relations with high accuracy despite higher training costs (9,224 seconds) [6]. Both approaches are limited by the availability and completeness of their respective knowledge sources, whether ontologies or annotated datasets.
Financial NLP and business intelligence also face substantial KAB challenges. Revisiting the Knowledge Injection Frameworks found that in financial NER, injecting aligned knowledge from sources like CnDbpedia and HowNet did not significantly outperform random knowledge injection, again pointing to Ineffective Knowledge Utilization by models [7]. This underscores a general problem in effectively leveraging specialized domain knowledge even when it is readily available. The Synthetic Knowledge Ingestion (Ski) method, however, demonstrated significant improvements in nDCG@1 and Recall@1 on the FiQA dataset for financial question-answering, suggesting that proper knowledge refinement and injection can overcome LLM domain knowledge deficits in specialized financial tasks [5]. Knowledge mechanisms in Large Language Models identifies finance and law as domains requiring sophisticated reasoning and decision-making based on specialized knowledge, with challenges stemming from data sparsity and diversity [30]. Natural Language Processing for Information Extraction notes that Business Intelligence (BI) tools rely on IE for data collection, extraction, and summarization, but future research needs to address noisy unstructured data and real-time stream data processing to enhance robustness [9].
Knowledge Graph Engineering (KGE) is also integral to industrial operations. Amazon’s AutoKnow system constructs a product KG for e-commerce, comprising over 30 million entities and 1 billion relations, utilizing an ontology suite for taxonomy enrichment (GNNs) and relation discovery, and a data suite for imputation and cleaning [3]. This highlights the use of hybrid methods, combining symbolic (ontology) and neural (GNNs, transformers) approaches. Standardizing Knowledge Engineering Practices also lists commercial settings and enterprise infrastructures as domains where KGE is applied, though often with custom architectures lacking standardized workflows [59]. Beyond specific applications, current_and_future_challenges_in_knowledge_representation_and_reasoning emphasizes the role of Knowledge Representation (KR) methods in information systems for ontology-mediated data access, data exchange, and data integration, as well as in Business Process Management (BPM) for modeling and analyzing complex, knowledge-intensive processes [29]. CEGA’s cost-effective GNN acquisition principles are also conceptually applicable to fraud detection, where GNNs are highly performant and efficient model acquisition is essential [45].
Limitations and Future Research in Industrial Operations: A significant limitation across industrial applications is the persistent Ineffective Knowledge Utilization where even available domain knowledge is not fully exploited by AI systems [7]. The challenges of expert dependency and maintainability for ontology-based methods, and computational costs and limited interpretability for ML-based methods, require further mitigation [6]. The need for IE techniques that can handle noisy and streaming data for real-time analytics remains an open problem in business intelligence [9]. Future work should focus on developing methods for LLMs to better understand and leverage complex domain knowledge structures in finance and law, particularly in the face of data sparsity and diversity [30].
Accurate knowledge acquisition is instrumental in socio-economic and environmental monitoring, where large-scale data analysis can yield critical insights for policy and humanitarian efforts. satellite_image_and_machine_learning_based_knowledge_extraction_in_the_poverty_and_welfare_domain extensively details the application of machine learning (ML) and deep learning (DL) models to extract knowledge about poverty and welfare from satellite imagery. These models, including Support Vector Machines (SVM), Random Forests, XGBoost, and various Convolutional Neural Networks (CNNs) like ResNet and Inception-Net, predict wealth indices, consumption expenditures, and poverty classifications. Often pre-trained on ImageNet and fine-tuned with night-time lights (NTL) or DHS data, these approaches achieve high predictive accuracy, sometimes explaining up to 85% of variation in survey-measured poverty. The tangible impact is the augmentation of traditional surveys, enabling higher spatial resolution poverty mapping and filling data gaps in data-scarce regions [39].
However, significant challenges persist. The primary limitation is the lack of scientific insight and interpretability, as models primarily focus on predictive performance without explaining “why” poverty exists or the causal relationships. The precise feature attribution from satellite imagery to socio-economic indicators remains opaque, leading to models potentially identifying “unexplained processes.” Most models are static, failing to address dynamic changes in poverty over time, and generalizability issues can arise across different indicators or the poorest regions [39]. The uncertainty_management_in_the_construction_of_knowledge_graphs_a_survey highlights that issues like timeliness (facts changing over time) and heterogeneous data sources are highly relevant to these dynamic and data-rich domains, requiring robust uncertainty management for accurate insights [55]. For environmental and health domains, Bench4KE’s benchmark dataset for Competency Question (CQ) generation includes projects focused on water and health, as well as health and climate services, illustrating the need for efficient ontology definition in interdisciplinary areas [14].
Limitations and Future Research in Socio-economic and Environmental Monitoring: The critical need is to move beyond predictive accuracy to interpretable and explainable models that can provide scientific insights into causal mechanisms. Future research should prioritize developing dynamic models to track changes over time and improve the generalizability of models across diverse geographical and socio-economic contexts. Addressing uncertainty management in KGs that integrate rapidly changing and heterogeneous data is also crucial [55].
Knowledge-based Visual Question Answering (KVQA) is a complex domain that necessitates multimodal reasoning and the integration of external world knowledge to answer questions that cannot be resolved from image content alone. The DKA framework addresses this by disentangling knowledge acquisition, leveraging LLMs for question decomposition and answer generation, PromptCAP for question-aware image captioning, and ChatGPT for external factual knowledge retrieval. This architecture explicitly tackles the issues of coupled knowledge acquisition, which leads to noise and confusion, and the implicit nature of LLM knowledge needs [61]. DKA achieved state-of-the-art performance on prominent KVQA benchmarks, with 62.1% accuracy on OK-VQA and 59.9% on AOK-VQA test sets, demonstrating significant improvements over previous LLM-based methods.
Limitations and Future Research in KVQA: The primary limitation identified in DKA is the insufficient ability of the caption model, particularly its susceptibility to multimodal hallucinations, which can propagate incorrect visual information and affect interpretability [61]. Future research should focus on improving caption models, potentially with LLM assistance, to generate more accurate and reliable visual descriptions, thereby enhancing the overall fidelity of KVQA systems.
Beyond the explicitly requested domains, knowledge acquisition techniques are applied across a multitude of other specialized fields.
Scientific Literature and Computer Science: The Knowledge AI framework fine-tunes NLP models like SciBERT for Named Entity Recognition on computer science publications (SciERC dataset), demonstrating superior performance on smaller datasets compared to BERT [2]. EneRex specifically extracts technical facets from computer science scholarly literature, including dataset usage, methods, and computing resources, enabling the discovery of trends like rising GitHub usage and shifts in deep learning framework popularity [51]. The unique challenge here is extracting nuanced technical information from full texts and dealing with data scarcity for novel facets. StructSense also applies NER term extraction from full-text neuroscience articles, utilizing an ontology database to provide semantic grounding for complex terminology, addressing data scarcity in neuroscience [70]. The SciNLP-KG framework focuses on constructing knowledge graphs for the NLP domain itself, extracting Tasks, Datasets, and Metrics, with potential generalizability to other scientific fields like computer vision or bioinformatics [11]. Graph-based Approaches and Functionalities in Retrieval Augmented Generation also details applications in scientific literature (DALK, ATLANTIC, KGP) for building domain-specific KGs and document graphs to improve retrieval faithfulness and relevance, as well as GraphCoder for code completion by integrating repository-specific knowledge into code LLMs [71].
Materials Science: MatSKRAFT provides a framework for large-scale materials knowledge extraction from scientific tables, covering domains from ceramics to nuclear materials. Its ability to identify rare property combinations is crucial for energy storage, electronics, and sustainable material development, directly addressing knowledge discovery in a data-intensive field [65].
Robotics and Autonomous Systems: A Survey of Behavior Learning Applications in Robotics highlights diverse applications in robotics beyond typical locomotion, including archery, playing with toys (Astrojax, Maracas), drumming, and calligraphy. These tasks involve acquiring knowledge about precise trajectories, force control, and rhythmic patterns, typically using imitation learning and policy refinement [64]. Knowledge Engineering Using Large Language Models conceptually extends to self-driving vehicles, acknowledging similar challenges in managing diverse forms of knowledge [52].
General Knowledge and Cultural Heritage: KGValidator applies its framework to general knowledge KGs like FB15K-237N and Wiki27K, achieving high accuracy with GPT-4 and web/Wikidata context [40]. Evo-DKD has been used for cultural heritage timeline modeling, extracting triples about historical events and artifact relationships [17]. Bench4KE includes cultural heritage projects for ontology-driven CQ generation [14]. Knowledge Graph Extension by Entity Type Recognition addresses the unique challenges of Chinese character KGs, managing semantic continuities and variations due to their evolutionary nature, and also demonstrates extending general KGs with domain-specific knowledge for local transportation and education systems [31].
Social Network Analysis and Cybersecurity: Large Graph Models are deemed critical for deriving insights from complex, graph-structured data in social network analysis, biological network analysis, and network security, often leveraging special pre-training mechanisms [12]. However, these models often do not outperform traditional small models in tasks reliant on structured knowledge like link prediction, indicating performance limitations for certain specialized graph analyses [12]. CEGA’s cost-effective GNN acquisition is conceptually applicable to fraud detection and healthcare diagnostics, addressing data sharing limitations and annotation costs [45]. In cybersecurity, KGs are constructed from log data to detect threats and vulnerabilities using frameworks like SLOGERT, which parse log files and utilize NLP for entity recognition [3].
Computer Vision: Net2Net accelerates the training of deep neural networks for image classification, demonstrating Net2WiderNet and Net2DeeperNet operations that significantly speed up convergence and achieve state-of-the-art accuracy on ImageNet, enabling efficient exploration of larger and deeper architectures [62]. Quantum Learning and Essential Cognition is applied to pedestrian re-identification, achieving high accuracy by addressing challenges of different data distributions and insufficient training data through continuous adaptation and robust feature learning [37].
Across these diverse applications, several cross-cutting limitations and areas for future research emerge. A pervasive challenge is the ineffective knowledge utilization by AI systems, where even readily available domain knowledge is not always effectively leveraged, particularly with knowledge injection techniques into LLMs [7]. This suggests a Knowledge Complexity Mismatch where current models struggle to integrate and reason with highly structured or nuanced domain knowledge. Data scarcity, especially for rare events or novel facets, remains a fundamental bottleneck, often requiring innovative solutions like targeted re-annotation strategies [21,25,51].
Interpretability and explainability are critical, especially in sensitive domains like healthcare and socio-economic monitoring, where model predictions need to be auditable and provide scientific insight rather than just high accuracy [21,39,50]. The timeliness and heterogeneity of data sources, coupled with the dynamic nature of many domains, demand robust uncertainty management in knowledge acquisition processes [55]. Furthermore, the generalizability of solutions across different contexts or subdomains, without extensive re-adaptation, continues to be a challenge, particularly for specialized domain KGs that may miss broader context [3].
Future research should prioritize the development of hybrid AI systems that can better integrate symbolic knowledge representation with sub-symbolic machine learning models to overcome the Knowledge Complexity Mismatch. Strategies for cost-effective expert involvement in data annotation and validation, as demonstrated by frameworks like PU-ADKA, are crucial for sensitive, expert-intensive domains [4]. Enhancing the robustness of IE tools to handle noisy and streaming data, particularly for real-time applications, is another vital direction. Finally, addressing ethical concerns and improving the reproducibility of domain-specific applications, especially in health, is paramount for building trust and facilitating wider adoption. This comprehensive landscape of applications underscores the sustained need for innovative, domain-aware approaches to tackle the KAB effectively.
6.8 Cross-Domain and Versatile Knowledge Acquisition
The challenge of acquiring knowledge that is both cross-domain and versatile is central to overcoming the Knowledge Acquisition Bottleneck (KAB), particularly in enabling systems to operate effectively in unfamiliar or “out-of-domain” contexts without extensive re-engineering. This demands frameworks and algorithms capable of robustly adapting to new data distributions, semantic structures, and architectural environments. Key to achieving this versatility are underlying assumptions about knowledge generalizability, theoretical foundations emphasizing transfer and invariance, and architectural choices that prioritize modularity and adaptive learning strategies.
Strategies for Cross-Domain and Versatile Knowledge Acquisition
| Strategy Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| General-Purpose World Knowledge | Leveraging broad, non-domain-specific knowledge. | Foundational for diverse applications, reduces domain-specific data needs. | Encyclopedic KGs (Wikidata, BabelNet), KNOW ontology, modular DeepKE. | Capturing nuances of specialized domains, ensuring semantic richness. |
| Transfer Learning | Adapting pre-trained models to new data/environments. | Bridges domain gaps, reduces data dependency, accelerates learning. | OOD generalization issues, architectural mismatch, interpretability bottlenecks. | |
| Domain Invariance | Disentangling semantics from nuisance factors. | Robustness to cross-domain variations (e.g., compilers). | Pluvio (CVIB for assembly clone search). | Assumes identifiable nuisance factors, potential loss of subtle context. |
| LLMs for Versatility | Instruction-driven learning, few/zero-shot capabilities. | Adaptability to diverse tasks, high generalizability. | Self-Tuning (cross-domain QA), AutoElicit (diverse priors), multilingual LLMs. | “Knowledge acquisition utilization gap,” hallucination, computational costs. |
| Agentic Problem-Solving | Abstracting experiences into transferable patterns. | Cross-domain experience sharing, improved complex problem-solving. | Agent KB (variable generalization, step compression). | Diminishing returns in highly dissimilar domains. |
| RL for Transferable Exploration | Learning generalizable exploration strategies. | Efficient adaptation to new environments without full retraining. | InfoBot (encoders for decision states), IBOL (skill discovery in MuJoCo). | Sim-to-real gap, designing effective reward functions. |
| Retrieval-Augmented Generation (RAG) | Grounding LLMs with external, structured KGs. | Robust and versatile KA across diverse domains. | Graph-based RAG (ATLANTIC, GraphCoder), SAC-KG (flexible KG construction). | Scalability of external memory, inference overhead, potential for semantic loss. |
A foundational principle for cross-domain versatility lies in leveraging general-purpose world knowledge that is not inherently tied to a specific domain [72]. Frameworks utilizing encyclopedic knowledge graphs (KGs) such as Wikidata, DBpedia, and BabelNet provide broad, multilingual semantic networks covering diverse topics and languages, serving as versatile sense inventories and foundational knowledge bases [1,3,10,55]. For instance, TeKGen leverages Wikidata for open-domain factual knowledge verbalization, demonstrating generalizability across various knowledge-intensive natural language processing (NLP) tasks [1]. Similarly, the KNOW ontology, built on “established human universals” like spacetime and social concepts, aims for broad applicability in real-world generative AI use cases, facilitating AI interoperability through code-generated SDKs for diverse programming languages [36]. The modular design of systems like DeepKE also supports customization across diverse tasks and domains by offering flexible components for data processing, model training, and evaluation [38]. The theoretical underpinning of invariance further promotes versatility by enabling models to adapt across situations, contexts, or environments, and to process diverse data types beyond traditional formats, through mechanisms like meta-learning and self-supervised learning [47]. The C^4 metacognitive modeling framework also conceptually emphasizes lifelong learning and adaptation of ontological concepts and lexical material for cross-domain human-AI interaction [58].
Transfer learning stands out as a primary mechanism for bridging domain gaps, especially through the use of pre-trained models. Pluvio exemplifies this by addressing the challenging “out-of-domain architectures and libraries” problem in assembly clone search [24]. Its framework leverages the all-mpnet-base-v2 sentence transformer, transferring general semantic understanding from natural language to assembly code. A critical architectural choice in Pluvio is the integration of a Conditional Variational Information Bottleneck (CVIB), which disentangles the semantic essence of assembly functions from “nuisance information” such as architecture and optimization settings. By conditioning on these factors during training to “forget” them, CVIB ensures that learned embeddings are invariant to cross-domain variations, thereby enhancing robustness to new, unseen environments. This approach achieves superior performance, with an AUC of 0.887 and an accuracy of 0.825 in out-of-domain scenarios [24]. Beyond binary code analysis, transfer learning from natural image datasets (e.g., ImageNet) to specialized visual domains like satellite imagery for poverty estimation also demonstrates its power, leveraging generalized visual feature detectors [39]. In scientific information extraction, models like SciBERT, pre-trained on extensive scientific corpora, exhibit robust generalization across various scientific sub-domains such as computer science and biology [2,51]. DeepKE also showcases cross-domain few-shot Named Entity Recognition (NER) by fine-tuning models on new textual styles and entity categories with limited data, achieving state-of-the-art results [38]. The concept of “universal thief datasets” is also explored in frameworks designed for extracting Deep Neural Networks (DNNs) across modalities. For instance, a framework successfully extracts DNNs for both image and text classification tasks by using distinct “universal thief datasets” (ImageNet for vision, WikiText-2 for NLP), highlighting adaptability to different data types and architectural variations with significant performance gains (e.g., 4.70x for image tasks, 2.11x for text tasks) [15].
Large Language Models (LLMs) inherently offer considerable versatility and generalizability due to their instruction-driven learning, zero- or few-shot capabilities, and capacity to handle diverse tasks [12,52]. Instruction tuning, which converts data from various tasks into unified instruction formats, significantly enhances LLMs’ generalization ability to new problems [12]. The Self-Tuning framework, for example, improves knowledge acquisition and retention by enabling LLMs to absorb knowledge from raw documents via a self-teaching strategy, demonstrating superior performance in multi-domain and cross-domain QA settings, with up to a 13% exact match improvement in cross-domain knowledge extraction [68]. AutoElicit further demonstrates versatility by generating informative priors for linear models across diverse clinical datasets (Heart Disease, Diabetes, UTI) and regression problems, improving predictive performance with fewer samples by leveraging the LLM’s “breadth of information across various domains” [19]. Multilingual approaches further extend versatility; BabelNet, a multilingual semantic network, integrates knowledge across 250+ languages and diverse sources, enabling cross-domain semantic annotation [10]. Methods like KRDL and multilingual vocabulary expansion improve the robustness of LLMs to Out-of-Vocabulary (OOV) issues across languages and tasks, facilitating knowledge transfer through English as an “interlingua” [16].
For complex agentic problem-solving, leveraging cross-domain experience is critical. The Agent KB framework facilitates this by employing an “experience abstraction pipeline” that transforms concrete experiences into abstract, transferable patterns through variable generalization, step compression, and domain neutralization [33]. This allows LLM-based reasoning to infer and apply domain-specific transformations, leading to improved success rates by up to 6.06 percentage points on general AI assistant tasks (GAIA) and significant improvements in software engineering code repair (SWE-bench) [33]. Similarly, the R1-Searcher++ framework demonstrates generalizability by applying learned knowledge acquisition strategies to out-of-domain multi-hop QA datasets and adapting to online web search environments, even when trained on local corpora [27]. This suggests robust and efficient knowledge acquisition strategies that bridge the gap between training and real-world inference. In reinforcement learning, InfoBot uses Conditional Variational Information Bottleneck (CVIB) to learn transferable exploration strategies across diverse environments (grid-world, Mujoco, Atari games), enhancing generalizability by learning encoders for decision states that are effective on unseen, more complex task variants without retraining the full policy [56]. IBOL also discovers skills across various MuJoCo environments by simplifying environment dynamics, enabling skill discovery across different systems without extensive re-engineering [35].
Retrieval-Augmented Generation (RAG), especially when enhanced with graph-based approaches, is crucial for robust and versatile knowledge acquisition across diverse domains [71]. Graph-based RAG frameworks like ATLANTIC integrate heterogeneous document graphs for interdisciplinary scientific tasks, enhancing retrieval coherence across scientific fields. GraphCoder utilizes a Code Context Graph to achieve language-agnostic code completion across Python and Java, effectively bridging domain-specific code knowledge into LLMs [71]. The generative capabilities of LLMs combined with structured KGs, as seen in SAC-KG and generative KGC methods, allow for flexible construction of KGs from diverse text corpora and across various domains like news, web content, and specialized fields, outperforming traditional Open Information Extraction (OIE) benchmarks [23,66]. GLM also shows state-of-the-art performance on out-of-domain question answering by leveraging self-supervised pre-training to inject structured knowledge implicitly into LMs, making them robust to knowledge from different but related domains [42].
Despite significant advancements, several limitations and challenges hinder truly versatile knowledge acquisition. Many approaches demonstrate versatility within specific sub-domains (e.g., within NLP, within scientific literature, or within robotics simulations), but fail to generalize to entirely different domains or data modalities without substantial re-engineering [37,48,70]. For instance, while DeepKE demonstrates multimodal integration, it does not explicitly detail theoretical aspects of robust adaptation mechanisms beyond empirical results [38]. The “black-box” nature of features transferred via transfer learning, as noted with ImageNet to satellite imagery, can obscure what knowledge is being leveraged, posing an interpretability bottleneck [39]. Similarly, AutoPrompt’s automatically generated prompts often “lack interpretability,” hindering understanding of why they work across domains [43].
A critical limitation in versatile knowledge application, even within known domains, is highlighted by the knowledge acquisition utilization gap in pretrained language models. Research indicates that while PLMs may acquire encyclopedic facts, they exhibit a “generalization gap” in knowledge utilization when faced with distributional shifts, specifically unseen relation types in downstream tasks [53]. This means that models often fail to generalize the application of their knowledge to novel relational patterns, even within the same broad domain of encyclopedic facts. This indicates a lack of robust versatility in applying learned knowledge dynamically, even when the underlying factual knowledge is present. This limitation is compounded by the phenomenon of knowledge entropy decay during LLM pre-training, where lower knowledge entropy in later stages negatively impacts the acquisition of new knowledge and increases forgetting, suggesting reduced versatility and generalizability for adapting to new information sources [69]. LLMs also face issues with hallucination, which limits their reliability and accuracy, especially for specialized or long-tail information, impacting their versatility [12,52]. The conversion of structured KGs to text for LLM processing can also lead to semantic loss, limiting the depth of versatile knowledge utilization [12]. Furthermore, many claims of versatility are theoretical or conceptual, lacking broad empirical validation across truly disparate domains, as observed in frameworks like Language Bottleneck Models [50], Quantum Learning [37], and Reference Architectures for KE [59]. The focus of current knowledge acquisition efforts often remains within specific problem classes (e.g., image-based classical planning in Latplan) rather than extending to diverse AI problems [28].
Future research needs to focus on quantifying and enhancing the robustness of cross-domain transfer mechanisms, developing domain-agnostic representations, and designing evaluation benchmarks that rigorously test versatility across fundamentally different data modalities and knowledge types. Addressing the “knowledge entropy decay” in LLMs and improving the effective utilization of acquired knowledge under distributional shifts are crucial for building truly robust and versatile knowledge acquisition systems.
7. Challenges, Limitations, and Future Directions
Despite remarkable advancements in artificial intelligence, the quest for truly intelligent systems capable of efficient and robust knowledge acquisition remains bottlenecked by a complex interplay of fundamental challenges. These impediments span technical limitations in system design, resource-intensive operational requirements, difficulties in ensuring trust and transparency, intricate human-AI interaction dynamics, and critical ethical and societal considerations. A comprehensive understanding of these challenges is essential for guiding future research toward developing more adaptable, intelligent, and responsible knowledge acquisition frameworks.
One major category of challenges revolves around bridging performance gaps in real-world deployment, encompassing issues of generalizability, robustness, and scalability [12,48]. Current AI models often struggle with Out-of-Distribution (OOD) generalization, exhibiting significant performance degradation on unseen or novel data, which limits their broader applicability, especially in specialized domains like operations and maintenance intelligence or robotics where a “reality gap” persists [48,64]. Architectural mismatches, where models fail to effectively process domain-specific structures or align internal knowledge representations with human cognitive structures, further compound these generalizability issues [12,48]. For Large Language Models (LLMs), a “persistent utilization gap” highlights that merely increasing model size does not guarantee effective knowledge application or robustness to distribution shifts, challenging the scalability hypothesis [53]. Moreover, the dynamic and ever-changing nature of real-world knowledge poses a significant challenge, as many knowledge base construction methods are “batch-like” and struggle with continuous updates and schema evolution [3,20].
A second core set of challenges stems from resource and data bottlenecks. The extreme data dependency of modern AI models, particularly LLMs, necessitates “internet-scale text with a word count in the trillions” for training, starkly contrasting with human few-shot learning abilities [26]. This leads to a severe annotation bottleneck, where acquiring vast quantities of high-quality, labeled data is expensive, time-consuming, and demands specialized human expertise [3,10,48]. The computational cost for training and updating large models is prohibitive, demanding “extensive cloud-based compute infrastructure” and incurring “prohibitive per-token costs” for operations, creating major scalability and sustainability concerns [18,20,65]. The quality and distribution of training data are paramount, as “improper learning data” is a “fundamental and primary cause” of knowledge fragility, leading to issues like insufficient representation of low-frequency facts and vulnerability to data noise [30]. Even the process of “high-quality prompt engineering” for LLMs has emerged as a direct, labor-intensive annotation bottleneck, underscoring the pervasive nature of this issue [12,52].
The third major challenge involves ensuring trust and understanding in AI systems. Many knowledge acquisition and extraction systems operate as “black boxes,” obscuring their internal decision-making and knowledge representations, which undermines user confidence and hinders debugging efforts [12,71]. LLMs frequently suffer from issues like hallucination, where they generate plausible but incorrect information, and inconsistent reasoning, severely impacting trustworthiness and explainability [2,12]. The “unreliability of parametric knowledge” and the “knowledge acquisition-utilization gap” further exacerbate these transparency issues, as models may possess factual knowledge but fail to apply it consistently or transparently [53]. A lack of provenance and reliability information for extracted knowledge also hinders validation in knowledge fusion approaches, impacting their trustworthiness [55]. While Knowledge Graphs (KGs) offer inherent interpretability due to their structured, symbolic nature, their construction is not immune to data quality issues, which can propagate implicit biases and inconsistencies [9,12].
A fourth area of concern lies in navigating the complexities of human-AI collaboration. Despite automation, human expertise remains indispensable for critical tasks such as prompt engineering, data curation, ontology development, and knowledge validation [12,70]. This human involvement, while crucial for refining systems and validating extracted knowledge, is often time-consuming, laborious, and costly, creating scalability issues for ubiquitous deployment [70,72]. The “human-AI knowledge gap” is a pervasive challenge, manifesting when AI’s internal representations diverge from human understanding, or when LLMs prioritize their internal, potentially outdated knowledge over provided context [12,20]. This gap also includes fundamental differences in human prior biases, divergent objectives, and computational capacities, as observed in human experts interacting with AI like AlphaZero [54].
Finally, the increasing power and pervasive application of knowledge acquisition systems bring critical ethical and societal implications to the forefront. The potential for AI to generate misinformation (e.g., hallucinations in LLMs) poses severe risks for scientific data dissemination and general knowledge provision [2,12]. Bias, embedded within vast training datasets or introduced through human input, can lead to unfair or skewed outcomes, necessitating robust mitigation strategies [19,32]. Privacy and intellectual property concerns are paramount, with risks ranging from verbatim memorization of training data by LLMs to model extraction attacks against proprietary AI systems [15,60]. Beyond technical vulnerabilities, responsible deployment demands consideration of safety (especially in robotics), sustainability (“Green AI”), and the ethical implications of human-AI interaction, including potential over-reliance and the commoditization of expert knowledge [51,54,64].
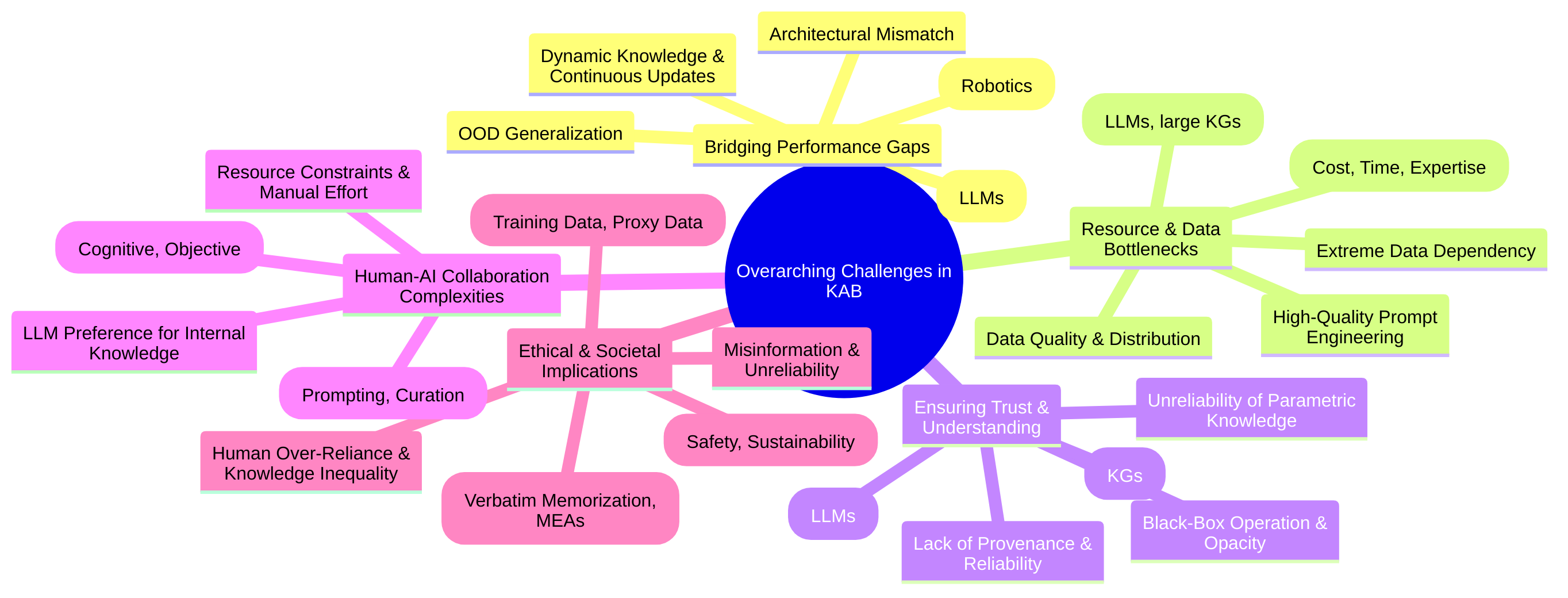
Addressing these interconnected challenges necessitates a concerted push towards innovative frameworks and future directions. Key areas of opportunity include the continued development of neuro-symbolic AI, integrating the strengths of LLMs with structured Knowledge Graphs to mitigate hallucinations, provide verifiable reasoning, and enable dynamic knowledge management [36,71]. Research into data-efficient and lifelong learning paradigms is critical, encompassing few-shot, zero-shot, active learning, and self-supervised strategies to alleviate annotation bottlenecks, alongside mechanisms for continual learning, forgetting, and knowledge evolution to handle dynamic environments [34,38,50]. Advancements towards intrinsically interpretable and steerable AI aim to move beyond surface-level explanations, focusing on architectures like Language Bottleneck Models and Concept Bottleneck LLMs that provide human-understandable representations and allow for direct human intervention and bias mitigation [32,50]. Fundamentally, all future work must prioritize responsible and sustainable AI development, embedding ethical guidelines, bias mitigation, privacy-preserving techniques, and resource-efficient models as core design principles, rather than afterthoughts [12,15]. Finally, fostering interdisciplinary research that leverages insights from cognitive science and other fields, coupled with the development of robust, dynamic evaluation benchmarks, is paramount for guiding progress and ensuring that knowledge acquisition systems serve humanity effectively and responsibly [14,30].
7.1 Generalizability, Robustness, and Scalability
The pursuit of artificial intelligence systems capable of acquiring and utilizing knowledge effectively is intrinsically linked to their generalizability, robustness, and scalability. These three properties represent fundamental challenges and benchmarks for evaluating the utility and applicability of any knowledge acquisition framework. Generalizability pertains to a system’s ability to perform well on unseen data or in novel environments, robustness concerns its resilience to noise, inconsistencies, or adversarial inputs, and scalability relates to its capacity to handle increasing data volumes, task complexities, or computational demands [12,48].
Generalizability, Robustness, and Scalability Challenges by Domain
| Challenge Type | Large Language Models (LLMs) | Knowledge Graphs (KGs) & IE Systems | Robotics & Autonomous Systems | Model Extraction & Security |
|---|---|---|---|---|
| Generalizability | OOD generalization, Persistent utilization gap, Limited context window. | Batch-like construction, schema evolution, limited dynamic updates. | “Reality gap” (sim-to-real), limited versatility of skills. | Architectural mismatch, specific sub-domains of transfer. |
| Robustness | Hallucination, knowledge conflicts, noisy external data, side effects of editing. | Noisy data, inconsistencies, dynamic consistency maintenance. | Unforeseen conditions, reproducibility of behaviors, hardware damage. | Adversarial inputs, noisy predictions as defense, transfer of functional knowledge. |
| Scalability | Prohibitive computational/per-token costs, retraining. | Manual effort, computational expense of ER, batch processing. | “Curse of dimensionality,” high energy consumption. | Query cost limits, computational cost of active learning. |
| Architectural Mismatch | Human-like vs. LM internal knowledge storage. | Lack of unified KG understanding, non-unified input formats. | Processing domain-specific structures, language for control. | Fidelity of extracted model based on architecture. |
| Data Resource Limitations | Requires “internet-scale text,” high computational cost. | Manual effort for construction, high cost for ER. | Sparse training data, robot wear/tear, costly real-world data. | High query budget, computational cost of active learning. |
A critical analysis reveals that many current methods often “over-adapt” to specific tasks, limiting their broader applicability and creating a significant bottleneck for further advancements [42].
A pervasive challenge across diverse AI domains is Out-of-Distribution (OOD) generalization, where models trained on one data distribution perform significantly worse when applied to a different one. In Knowledge Extraction (KE) for operations and maintenance, off-the-shelf NLP tools show “significantly lower” performance on domain-specific datasets due to uncommon syntax, shorthand, and acronyms, underscoring a severe OOD generalization issue [48]. Similarly, traditional machine learning models often “overfit to a specific domain they are trained based on” [72]. Robotic systems exhibit a pronounced “reality gap,” where behaviors learned in simulation fail to generalize to physical robots due to unmodeled dynamics [64]. This problem extends to open-world models, which struggle with domain transfer due to “significant differences in data distribution and feature representation” [37].
Another core impediment is architectural mismatch, which manifests in various forms. The inability of general NLP models to process domain-specific linguistic structures or “out-of-domain architectures and libraries” is a form of architectural mismatch requiring specialized adaptation [48]. In knowledge graph (KG) construction, the absence of a unified understanding of what a KG entails leads to a lack of robustness to varied input formats [74]. For language models (LMs), the internal knowledge storage mechanisms often differ from human cognitive structures, hindering controllability and complex associative reasoning [12]. The assumption of a “quasi-static knowledge state” in Language Bottleneck Models (LBMs) also presents an architectural mismatch with dynamic, evolving student knowledge over time [50].
Computational and data resource limitations present cross-cutting issues that hinder progress across all domains. The sheer scale of modern AI, particularly Large Language Models (LLMs), demands “extensive cloud-based compute infrastructure” and incurs “prohibitive per-token costs” for operations such as knowledge extraction [18,65]. Retraining LLMs to incorporate new knowledge is “prohibitively expensive” and environmentally unsustainable, creating a major scalability bottleneck for dynamic updates [20]. Even for smaller models, active learning strategies that involve retraining in each round are computationally intensive, requiring thousands of training runs [57]. Robotics, in particular, faces high energy consumption for large models and real-time control, along with the “curse of dimensionality” as state-action spaces expand dramatically for complex systems [64].
Challenges in Large Language Models (LLMs) are particularly acute in the context of generalizability, robustness, and scalability. Despite their large parameter counts, LLMs face a “persistent utilization gap,” meaning that simply increasing model size does not proportionally improve the amount of knowledge that can be effectively utilized [30,53]. This gap, coupled with a lack of robustness to distribution shifts, impedes their reliability as knowledge sources [53]. LLMs frequently exhibit robustness issues such as hallucination, knowledge conflicts (favoring internal, potentially outdated, knowledge over external context), and susceptibility to noisy external data [2,12]. Knowledge editing, while promising, can lead to “side effects” that impair general capabilities and exhibit limited propagation of edited knowledge, posing generalizability challenges [20,30]. Furthermore, LLMs are constrained by “limited context window” sizes, restricting their ability to process lengthy documents or complex interactions [36,65]. Research on knowledge mechanisms and interpretability is also often “restricting analysis to smaller models” due to computational constraints, raising questions about the generalizability of findings to much larger LLM architectures [30,34].
Knowledge Graphs (KGs) and Information Extraction (IE) systems also grapple with significant challenges. For KGs, manual effort for construction and maintenance limits scalability, making them “costly and time-consuming” [55]. Most current KG construction pipelines are “batch-like,” leading to “enormous amount of redundant computation” and hindering continuous updates [3]. Entity resolution within KGs is “computationally expensive because the number of comparisons between entities typically grows quadratically” [3]. The evolution of KG schemas and the integration of emerging entities present continuous generalizability challenges [3]. Robustness is compromised by noisy data, inconsistencies, and the difficulty of maintaining consistency in dynamic, large KGs [3,55]. DeepKE, an IE toolkit, demonstrates improved robustness to low-resource settings and generalizability to complex, multimodal data by offering few-shot capabilities and supporting document-level extraction [38]. However, MatSKRAFT’s domain-specific optimizations for materials knowledge extraction suggest generalizability issues for other scientific fields without substantial re-engineering [65]. The SciNLP-KG framework, while demonstrating strong scalability by constructing a large KG, faces domain generalizability issues as it is specialized for NLP and its claims for other domains remain unverified [11].
In the domain of robotics, the “reality gap” stands out as a major generalizability limitation, as behaviors learned in simulation rarely transfer seamlessly to physical systems [64]. Coupled with the limited versatility of learned skills (e.g., bipedal walking only in controlled environments), scaling robotic intelligence to diverse real-world scenarios remains difficult [64]. Robustness in robotics is challenged by unforeseen conditions, the difficulty of reproducing learned behaviors, and the complex problem of adapting to hardware defects or “injuries” [64]. Comparing this to AI agents like AlphaZero, the challenge of learning robust latent representations is evident in Latplan’s “Symbol Stability Problem,” where latent propositions can randomly flip, hindering planning and robustness under noisy inputs [28]. Furthermore, AlphaZero’s concept discovery framework is limited to linear sparse concept vectors, and faces scalability challenges for human evaluation of its learned concepts [54].
Model extraction and security present another domain with distinct generalizability, robustness, and scalability concerns. Model extraction attacks, such as those discussed in [15], highlight an “architectural mismatch” where the fidelity of an extracted model is highest when its architecture mirrors that of the target model. Divergent complexities between secret and substitute models can degrade performance, though “reasonably high” agreement can still be achieved, suggesting some generalizability [15]. The “OOD performance” of Pluvio, an assembly clone search tool, demonstrates a more successful approach to generalizability and robustness by tackling “out-of-domain architectures and libraries” through transfer learning and conditional variational information bottleneck, achieving significant improvements (e.g., 35% accuracy increase in OOD settings) [24]. Scalability in model extraction is often limited by the “computational cost” of active learning strategies and stringent query budgets, with “excessive querying” leading to “substantial computational and financial costs” and security alerts [15,45].
Synthesizing these challenges, several overarching themes emerge:
- The difficulty of capturing ever-changing world knowledge: LLMs struggle with knowledge conflicts and side effects during updates, and existing knowledge editing methods show “little propagation of edited knowledge” [20]. KG construction methods are often batch-oriented, lacking robust mechanisms for continuous, dynamic updates and schema evolution [3].
- The complexity of learning robust latent space representations: Deep latent models, such as Latplan, face a “Symbol Stability Problem” where latent propositions can randomly flip, leading to disconnected search spaces and interpretability concerns [28]. This highlights the challenge of ensuring learned representations are stable and reliable.
- The scalability of graph-based approaches: While KGs offer rich knowledge representation, their construction and maintenance pose significant scalability issues, especially for real-time updates and consistency across large, dynamic datasets [3,55]. Graph-based RAG systems, for instance, struggle to maintain performance with expansive and intricate KGs due to processing speed and resource usage [71].
- The “persistent utilization gap” and the lack of “robustness to distribution shifts”: These fundamental issues critically impede the scalability and generalizability of Pre-trained Language Models (PLMs) as reliable knowledge sources, despite their growing parameter counts [53]. This means that merely increasing model size does not guarantee effective knowledge application, challenging the scaling hypothesis.
- Scaling mechanistic interpretability findings: The computational constraints and methodological limitations of current circuit discovery methods restrict analyses to smaller models, questioning the generalizability of findings to very large LLM architectures [30,34].
Common hurdles in transitioning from theoretical efficacy to broad practical applicability include the high computational costs of training and inference, especially for LLMs and complex robotic systems [12,51]. The reliance on specialized hardware, extensive datasets, and manual effort for annotation or domain adaptation often limits widespread deployment [10,25]. Furthermore, frameworks can “over-adapt” to specific tasks, diminishing their generalizability to other downstream applications [42].
Future research directions should prioritize developing more resource-efficient models, particularly for LLMs, to mitigate their substantial computational footprints and enable wider adoption [20,65]. Leveraging transfer learning effectively, as demonstrated by Pluvio for OOD architectures in binary analysis, and Self-Tuning for knowledge acquisition strategies across LLM architectures, is crucial for improving generalizability to new domains and tasks [24,68]. Developing novel data augmentation strategies and robust data filtering mechanisms are essential for improving models’ robustness to noisy or insufficient data, as highlighted by challenges in IE and sense-annotated corpora [10,25]. Advancements in neuro-symbolic approaches, such as KNOW, aim to balance expressiveness with computational tractability for improved scalability and generalizability [36]. Furthermore, the establishment of comprehensive, multi-domain benchmarks is vital to accurately assess and compare generalizability and robustness across diverse systems, moving beyond synthetic evaluations to real-world applicability [14,74]. Addressing these interconnected challenges will be paramount for pushing the boundaries of knowledge acquisition in AI.
7.2 Data Dependency and Annotation Bottleneck
The pervasive challenge of data dependency and the annotation bottleneck fundamentally constrains knowledge acquisition in artificial intelligence systems, spanning various domains from natural language processing to robotics. This bottleneck manifests as a critical need for vast quantities of high-quality, labeled data, which is inherently expensive, time-consuming, and often requires specialized human expertise to produce [3,6,10,12,23,25,29,41,48,52,57,70,72,74]. Traditional artificial neural networks (ANNs) and modern large language models (LLMs) are notoriously data-hungry, with LLMs requiring “internet-scale text with a word count in the trillions” for training, starkly contrasting with human few-shot learning abilities [26].
Mitigating Data Dependency and Annotation Bottleneck
| Strategy Category | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| Data-Efficient Learning | Minimizes reliance on extensive labeled data. | Reduces annotation cost/time, enables learning from fewer examples. | Still requires some labeled data, may not cover extreme scarcity. | |
| Few-shot/Zero-shot Learning | Learns from very few or no labeled examples. | Reduces manual annotation drastically, especially for NER/RE. | DeepKE (few-shot NER/RE), AutoElicit (LLM priors), KRDL (zero-shot EL). | Performance drop compared to full supervision, often needs proxy labels. |
| Self-Supervised Learning | Exploits intrinsic patterns in unlabeled data for automatic labels. | Mitigates annotation dependency, uses vast raw data. | IBOL (skill discovery), Self-Tuning (knowledge-intensive tasks), KG-guided pre-training. | Quality of auto-derived labels, still needs data for pre-training. |
| Active Learning (AL) | Iteratively selects most informative samples for human annotation. | Optimizes annotation budgets, reduces data requirements significantly. | Uncertainty sampling (Deep Bayesian AL), PU-ADKA (expert selection), CEGA (GNN sampling). | Computational cost of retraining, optimal acquisition function selection. |
| Data Distribution & Quality Management | Ensures balanced, high-quality data for robust learning. | Prevents knowledge fragility, ensures sufficient representation of facts. | Data augmentation/filtering, targeted re-annotation, LLM prompt generation. | Identifying/mitigating bias, data leakage, “more is not better” without purity. |
| Addressing Prompt Engineering Bottleneck | Automates/optimizes prompt generation for LLMs. | Reduces laborious manual effort, improves elicitation efficiency. | AutoPrompt (gradient-guided search), HIL for prompt refinement (StructSense). | Prompts can be uninterpretable, brittleness, still requires labeled data for optimization. |
| Annotation Strategy Optimization | Improves efficiency and quality of human annotation. | Reduces cost, time, and errors in labeled data creation. | Targeted re-annotation (confidence-based ranking), HIL (StructSense). | Resource constraints, human bias, scalability of crowdsourcing. |
| Leveraging Pre-trained Knowledge | Transfers broad knowledge from large models. | Reduces need for domain-specific labeled data. | Pluvio (MPNet for binary analysis), SciBERT (domain pre-training), RetroPrompt. | OOD generalization issues, architectural mismatch, requires large base models. |
This extreme data demand highlights a significant resource constraint and an annotation bottleneck that impedes the development of robust, generalizable knowledge acquisition systems.
Ongoing efforts to develop more data-efficient learning paradigms directly tackle this annotation bottleneck. Few-shot learning, for instance, enables Named Entity Recognition (NER) and Relation Extraction (RE) with as few as 8 to 16 labeled instances, significantly reducing reliance on extensive manual annotation [38]. Methods like AutoElicit further reduce the sample complexity of predictive models by leveraging informative priors from LLMs, saving substantial labeling effort, with one case quantifying a saving of “over 6 months of labeling effort” to achieve comparable accuracy with 15 labels [19]. GPT-3’s in-context learning also offers notable savings by utilizing few-shot examples [18]. Language Bottleneck Models (LBMs) achieve comparable accuracy to state-of-the-art Knowledge Tracing methods with “orders-of-magnitude fewer student trajectories,” demonstrating effective generalization from minimal examples [50]. Zero-shot learning, as explored by the KRDL framework, aims to achieve “zero manually labeled examples” for tasks like biomedical entity linking by unifying weak supervision, thereby leveraging distant supervision to reduce direct annotation needs [16]. Episodic memory further enables zero-shot augmentation for LLMs, allowing dynamic acquisition of new factual knowledge without retraining or new labeled data for every fact [16].
Self-supervised learning offers another powerful avenue to mitigate annotation dependency by exploiting intrinsic patterns in raw, unlabeled data. This approach formulates “pretext tasks” where labels are automatically derived, tapping into “untapped potential” in raw data to reduce the burden of human-annotated labels [47]. Examples include unsupervised skill discovery methods like IBOL, which operates without external rewards or human-annotated behaviors, discovering skills solely from environmental interactions [35]. The Self-Tuning framework, using a Self-Teaching strategy, augments documents with self-supervised knowledge-intensive tasks, generating learning tasks automatically from raw text without additional annotation costs [68]. Similarly, leveraging existing Knowledge Graphs (KGs) to guide learning from raw text through self-supervised tasks reduces the reliance on extensive human-annotated data for structured knowledge acquisition [42].
Active learning strategies are instrumental in optimizing annotation budgets by interactively querying an oracle for uncertain or informative predictions. This approach is particularly effective in reducing data requirements for deep learning models, which often exhibit “extreme data-dependence” [57]. For instance, active learning can reduce the labeled data needed by up to 2.5 times compared to random sampling for tasks like NER, significantly alleviating the annotation bottleneck [57]. In the context of specialized domains with costly expert input, PU-ADKA efficiently integrates expert feedback by strategically selecting and querying the most appropriate expert, maximizing the value of each annotated data point within a fixed budget [4]. Future research for classical planning models like Latplan also anticipates active learning to relax uniform sampling requirements and improve data efficiency [28].
The critical role of data distribution and quality for robust knowledge acquisition and model operation cannot be overstated. “Improper learning data,” in terms of both its distribution and quantity, is identified as a “fundamental and primary cause” of knowledge fragility in LLMs [30]. LLMs tend to prioritize memorizing “more frequent and challenging facts,” which significantly hinders the memorization of low-frequency facts and leads to “insufficient representations” for such knowledge [12,20,30,34,40,55,69,73]. This “positive correlation with knowledge frequency” highlights a subtle yet critical form of data dependency even in highly autonomous learning systems, pointing to the need for balanced or adaptive data sampling strategies to prevent a “scarcity of data and low cognitive confidence” leading to “imbalanced data samples” [37]. Even small amounts of data in the post-training stage can compromise the robustness of knowledge representation, necessitating “sufficient augmentation” through paraphrasing or sentence shuffling during pre-training to make knowledge extractable and applicable [30,73]. Moreover, knowledge quality is paramount; “more does not mean better without controlling knowledge purity,” as injecting excessive or overly complex knowledge can lead to performance degradation [7]. Data leakage and noise are also significant concerns, with synthetic data generation potentially introducing “noise” and “reward signal misalignment” [63]. Robust knowledge acquisition systems require careful monitoring of data quality and consistency [59].
The challenge of “high-quality prompt engineering being time-consuming and laborious” has emerged as a direct annotation bottleneck in the era of LLMs [12,20,30,52]. This task, akin to traditional knowledge engineering, demands significant human effort and ingenuity to craft effective prompts for knowledge elicitation [26]. While methods like AutoPrompt aim to automate prompt generation, they often still require labeled data for their optimization phase, shifting rather than eliminating the data dependency [43]. Even in self-supervised learning frameworks, initial evaluation datasets might involve “handcrafted prompts” for LLM-based generation [68].
The efficacy of different annotation strategies significantly impacts human effort and data quality. For specialized domains, the ideal approach of using “multiple annotators” and “adjudication” for high-quality data is often not feasible due to “resource constraints,” making manual annotation a time-consuming and expensive activity [25]. Single annotation, while cheaper, can lead to “inconsistencies or errors” that degrade model performance significantly (e.g., a 9.8% F-score drop for BioBERT) [25]. Solutions include intelligently sampling for targeted second annotation, where selectively re-annotating a subset of data (e.g., 7.5% or 37.6%) can significantly reduce the performance gap without the full cost of double annotation [25]. Human-in-the-loop (HIL) approaches, exemplified by StructSense, enable humans to correct and guide LLM outputs, serving as an efficient method for refining generated data rather than undertaking extensive manual annotation from scratch [70]. Crowdsourcing, while providing “cheap labels” for simple tasks, struggles with complex or diverse data, highlighting its limitations in fully addressing the annotation bottleneck [72].
The trade-offs between model complexity, data requirements, and performance in knowledge acquisition are evident across various domains. In robotics, data demands are extreme due to sparse training data, robot wear and tear, sample inefficiency (e.g., 100 years of experience for in-hand manipulation), and the difficulty of acquiring data for dangerous situations [64]. The “reality gap” further limits the utility of simulated data, necessitating real-world data collection which is often labor-intensive and costly due to continuous human supervision [64]. Strategies like lifelong learning, knowledge transfer, and bootstrapping are proposed to mitigate these challenges, enabling systems to efficiently reuse knowledge across tasks [64]. Unsupervised skill discovery methods like IBOL also address this by operating without external rewards, making them suitable for sparse-reward environments inherent to robotics [35].
Conversely, in game AI, data-efficient concept learning has been explored using AlphaZero’s (AZ) self-play games and Monte Carlo Tree Search (MCTS) statistics to discover novel, machine-unique concepts without relying on human labels. This reduces data dependency for discovery, though validation still relies on “human crafted datasets” and “human experts” [54]. Latplan also tackles the annotation bottleneck in classical planning by learning from “unlabeled image pairs” rather than manual symbolic modeling, though it introduces new data dependency challenges related to uniform sampling and feature imbalance [28]. InfoBot implicitly addresses data scarcity in sparse reward environments by generating intrinsic motivation, thereby reducing the need for meticulously designed reward functions [56].
Comparing active learning for model extraction versus leveraging vast pre-trained knowledge for transfer learning reveals distinct approaches to data efficiency in resource-scarce specialized domains. In model extraction, active learning strategies like those employed by [15] are used to minimize queries to Machine Learning as a Service (MLaaS) models, effectively reducing the “computational cost” for an adversary seeking to replicate a model. This framework leverages large, public “universal thief datasets” and active learning to select a small yet informative set of samples, achieving significant query efficiency (e.g., 4.70x for image, 2.11x for text) over uniform noise baselines [15]. Similarly, CEGA applies active sampling for Graph Neural Networks (GNNs) to train high-performing models with minimal supervision, tackling the annotation bottleneck in biomedicine by selectively sampling informative nodes [45]. This contrasts with a broader application of active learning, which focuses on reducing annotation for training new models.
For resource-scarce specialized domains, transfer learning leveraging vast pre-trained knowledge is a powerful strategy. Pluvio, for example, mitigates data scarcity for “low-resource or proprietary processor toolchains” by utilizing “human common knowledge through large-scale pre-trained natural language models” for assembly clone search, reducing direct dependence on extensive domain-specific labeled data [24]. Domain pre-training, such as SciBERT, significantly impacts knowledge acquisition in K-Shot scenarios for extractive Question Answering, outperforming general models like BERT, especially when data size is low [2]. Cross-domain adaptation, a feature of tools like DeepKE, further helps mitigate the annotation bottleneck by generalizing from source domain knowledge to new domains with minimal data [38]. The use of proxy labels, such as night-time lights for poverty estimation from satellite imagery, is another form of transfer learning that indirectly addresses the annotation bottleneck by leveraging readily available (though imperfect) signals to fine-tune pre-trained models [39]. The RetroPrompt approach also decouples knowledge from memory by training an external knowledge base independently, reducing reliance on the LLM’s internal “mechanical memorization” for long-tailed samples and thereby reducing data dependency for the main model [12].
Despite significant advancements, several limitations and areas for future research remain in addressing data dependency and the annotation bottleneck. The solutions proposed in [16], while effective in reducing annotation needs, still face challenges such as improving denoising strategies for evidence extraction and overcoming difficulties in multilingual alignment. Human annotation remains complex for intricate tasks, where even human ground truth might be incomplete. Generating zero-shot prompts efficiently without any labeled data is still an open question [43]. The internal dynamics of LLMs, such as the decay of “knowledge entropy” during pretraining, reduce their efficiency in acquiring new knowledge, implying a need for methods to guide active learning strategies by selecting data points that most effectively impact knowledge retention and update [69]. Autonomous mechanisms for identifying outdated knowledge and triggering updates are also largely unaddressed [20]. Future work needs to focus on managing severe data imbalance or extreme scarcity for truly novel classes, especially in semi-supervised settings where initial samples are rare [37]. Developing scalable and automated methods to “purify and prune” knowledge from existing knowledge bases is crucial for improving knowledge quality and utilization by LLMs [7]. Additionally, extending self-supervised learning to entirely new domains lacking pre-existing KGs and adapting classical planning models to learn from sparse or noisy real-world data streams are critical research directions [28,42]. Overcoming the reliance on “universal thief datasets” in model extraction for highly niche or proprietary domains, and quantitatively assessing the cost reduction by data-efficient paradigms, represent further research opportunities [15,47]. The long-standing problem of creating new resources (corpora, benchmarks, KGs) also remains fundamental, particularly for ensuring robust out-of-domain generalization and fair evaluation of novel approaches [74].
7.3 Interpretability and Transparency
Achieving interpretability and transparency in knowledge acquisition and extraction systems is paramount for fostering trust, enabling refinement, and ensuring the ethical deployment of AI technologies [29,39]. Current knowledge acquisition and extraction systems frequently operate as “black boxes,” obscuring the decision-making processes and internal knowledge representations, which undermines user confidence and hinders debugging efforts [12,71].
Interpretability and Transparency in Knowledge Acquisition
| Challenge / Approach | Core Mechanism / Goal | KAB Addressed / Benefit | Key Tools / Examples | Limitations / Challenges |
|---|---|---|---|---|
| LLM Opacity Challenges | Inherent black-box nature, unreliability of parametric knowledge. | - | Hallucination, utilization gap, inconsistent reasoning, opaque prompts. | Undermines trust, hinders debugging, limits high-stakes adoption. |
| Probing Techniques | Reveal linearly encoded knowledge within hidden states. | Diagnostics for internal representations, insights into knowledge storage. | P-Probing, Q-Probing (LLM hidden states). | Limited to linear interpretability, does not explain complex reasoning. |
| Mechanistic Interpretability (MI) | Reverse-engineers internal computations of neural networks. | Deeper understanding of how knowledge is acquired/processed. | Knowledge Circuits (EAP-IG), Knowledge Entropy (FFNs). | Computationally intensive, often limited to smaller models, difficult to translate to human terms. |
| Intrinsically Interpretable Architectures | Designs models to be interpretable by nature. | Provides human-understandable explanations & steerability. | Language Bottleneck Models (LBMs), Concept Bottleneck LLMs (CB-LLMs). | Architectural constraints, potential for oversimplification, trade-offs with performance. |
| Explainable AI (XAI) Principles | Presents AI predictions in human-understandable form. | Enhances trust, enables scientific insight, aids debugging. | Attribution Maps (GradCam), Feature importance, KGValidator (reasons), StructSense (ontologies). | Often surface-level, may not capture true causality, computational cost. |
| Knowledge Graphs (KGs) | Structured, symbolic representation of knowledge. | Inherent interpretability, traceable reasoning, factual grounding. | KG triples, OWL, SHACL. | Construction not immune to quality issues, may not explain neural processes. |
| Neuro-Symbolic Integration | Combines neural learning with symbolic reasoning. | Balances pattern recognition with explainable reasoning. | LRNLP, Evo-DKD (structured edits + natural language justifications). | Complexity of integration, ensuring consistent interplay between components. |
| Concept Discovery (Game AI) | Extracts human-interpretable concepts from AI latent space. | Bridges human-AI knowledge gap, makes AI strategies transparent. | AlphaZero (concept puzzles for grandmasters). | Limited to specific domains, relies on human expert validation. |
| Uncertainty Quantification | Estimates model confidence in predictions. | Provides transparency on reliability, guides decision-making. | Confidence scores, probability distributions. | May not reflect true uncertainty, can be opaque for complex models. |
A primary limitation of contemporary knowledge acquisition and extraction systems stems from the inherent opacity of deep learning models. In Large Language Models (LLMs), this manifests as the “unreliability of parametric knowledge” and the “knowledge acquisition-utilization gap” [53], where a model might possess factual knowledge but fail to consistently or transparently apply it in reasoning, leading to unreliable outputs and a lack of transparency [20,73]. This gap can be attributed to the implicit nature of knowledge storage, contrasting sharply with the explicit and human-readable nature of symbolic knowledge representations [72]. Furthermore, LLMs frequently exhibit issues such as hallucination, generating plausible but incorrect information, and inconsistent reasoning, which severely impacts trustworthiness and explainability [2,12,52]. Techniques like AutoPrompt, while effective for knowledge elicitation, often generate semantically opaque prompts, further contributing to the interpretability deficiency of LLMs [43]. The internal mechanisms of knowledge injection in LLMs are also challenged, with evidence suggesting that injected knowledge often doesn’t form distinct internal representations, leading to ineffective utilization and opaqueness about how specific knowledge content is processed [7].
To address these challenges, several approaches focus on enhancing interpretability. Probing techniques, such as P-probing and Q-probing, attempt to reveal how knowledge is linearly encoded within LLM hidden states, providing insights into specific knowledge storage locations and their linear extractability [73]. While useful for diagnosing internal representations, these methods are often limited to linear interpretability and do not fully demystify non-linear reasoning processes or provide human-understandable explanations for complex decisions [73].
Mechanistic interpretability offers a deeper understanding by reverse-engineering the internal computations of neural networks. Studies have successfully identified “knowledge circuits”—computational subgraphs within LLMs—that govern knowledge acquisition. This research reveals a “deep-to-shallow pattern” of knowledge acquisition and the functional roles of specialized components, such as distinct attention heads (e.g., mover, relation, mixture), thereby increasing transparency into how knowledge is stored and processed within the model [30,34]. The concept of knowledge entropy further provides a mechanistic measure of how LLMs utilize their internal parametric knowledge, explaining why models may struggle with new knowledge acquisition or exhibit increased forgetting by analyzing the broadness of memory vector engagement in feed-forward layers [69]. This quantitative approach contributes to understanding the internal confidence or spread of knowledge activation, although it needs further integration with human-understandable explanations [69].
Frameworks like Language Bottleneck Models (LBMs) and Concept Bottleneck Large Language Models (CB-LLMs) represent significant advancements towards intrinsically interpretable knowledge systems. LBMs provide human-understandable representations of student knowledge states by forcing all predictive information through a concise natural-language bottleneck, offering faithful and steerable summaries for knowledge tracing. This contrasts with traditional knowledge tracing methods that rely on opaque, high-dimensional latent vectors and LLM-based approaches prone to hallucination [50]. Similarly, CB-LLMs integrate a Concept Bottleneck Layer (CBL) that compels LLMs to represent information using human-interpretable concepts, yielding faithful explanations and transparent decision-making. This architectural choice directly addresses the “inherent opacity” of LLMs, enabling user control and promoting safer, more reliable outputs [32].
The integration of explainable machine learning (XAI) principles is crucial across domains. In areas like socio-economic analysis based on satellite imagery, interpretability and explainability are critically underdeveloped, making it difficult to trust or act upon AI-derived insights. True explainability demands understanding relationships encoded in the model using domain-specific concepts, moving beyond mere attribution maps to address “what, how, and why” questions about causality [39]. The need for explainable AI is universal, extending to systems like StructSense, which provides principled, interpretable outputs through ontologies and human-in-the-loop evaluations, and KGValidator, which outputs explicit reasons for validation decisions, enhancing the transparency of knowledge graph construction [40,70].
In specialized domains, interpretability challenges and solutions vary. Learned robotic behaviors, particularly those involving reinforcement learning, often lack interpretability due to emergent properties and “reward hacking,” where robots achieve goals in unintended or unsafe ways. The inability of robots to explain their actions hinders trust and human-robot collaboration [64]. Efforts to bridge this “human-AI knowledge gap” include concept discovery in game AI, such as making AlphaZero’s internal knowledge transparent by extracting concepts and presenting them through “puzzles” that human experts can understand and generalize from [54]. The InfoBot framework also offers conceptual interpretability by identifying “decision states” where an agent makes goal-dependent choices [56]. Similarly, in binary code analysis, methods like Conditional Variational Information Bottleneck (CVIB) in Pluvio contribute to an interpretable and invariant latent space by disentangling core functional semantics from domain-specific “nuisance information” [24]. The IBOL framework likewise promotes disentanglement in skill latents for interpretable skill discovery in unsupervised settings [35].
Knowledge Graphs (KGs) are inherently interpretable due to their structured, symbolic nature, offering traceable reasoning and human-centric understanding, which LLMs often lack due to their fully parameterized, implicit knowledge storage and proneness to hallucination [12,74]. Combining LLMs with KGs has been shown to improve factual correctness and explanations, promoting quality and interpretability of AI decision-making [3,36]. This neuro-symbolic integration, exemplified by Logical Reasoning over Natural Language (LRNLP), offers stepwise interpretability, contrasting with the opacity of end-to-end neural methods [75]. Other systems like Evo-DKD enhance interpretability by providing structured ontology edits with natural language justifications, improving trust in AI-curated knowledge bases through transparent self-reflection mechanisms [17].
Despite these advances, significant limitations persist. Interpretability is often at the output level (e.g., verbalized text from KGs [1], PDDL output from planning systems [28], or structured information from Information Extraction [9,11]), rather than deep mechanistic interpretability of the AI models themselves [44,66]. The ability of LLMs to generate explanations does not always guarantee true conceptual understanding, as shown by models fabricating agreeable responses rather than accurately assessing validity [40]. Furthermore, the lack of provenance and reliability information from LLMs regarding extracted knowledge is a severe interpretability limitation, hindering trustworthiness and validation in knowledge fusion approaches [55]. Even when models predict well, they can yield “intuitively inconsistent” results that are difficult to explain, highlighting a persistent interpretability gap [39].
Future research directions must focus on developing more transparent knowledge-based AI systems. This includes creating novel methods for mechanistic interpretability that can translate complex internal mechanisms into human-understandable terms, developing more robust evaluation metrics for human interpretability and explanation fidelity, and enhancing the inherent transparency of knowledge acquisition processes by designing architectures and training processes that promote modularity, sparsity, and monosemanticity [30]. Addressing the “unreliability of parametric knowledge” and the “utilization gap” remains a fundamental challenge, requiring further investigation into how LLMs can consistently apply their acquired knowledge transparently. Moreover, there is a need to develop standardized approaches for tracking provenance and certainty in knowledge graphs derived from diverse sources, particularly LLMs, to improve their reliability and trustworthiness [55]. Bridging the gap between a model’s effectiveness and its human comprehensibility will necessitate continued interdisciplinary efforts, leveraging insights from cognitive science and human-computer interaction to build AI systems that are not only powerful but also truly understandable and accountable.
7.4 Human-in-the-Loop and Human-AI Collaboration
The persistent challenge of knowledge acquisition, even amidst rapid advancements in automation, underscores the continuing necessity for human involvement and supervision.
Challenges in Human-AI Collaboration for Knowledge Acquisition
| Challenge Category | Description / Manifestation | Impact on Knowledge Acquisition | Key Examples / Contexts |
|---|---|---|---|
| Resource Constraints & Manual Effort | Initial KA tasks remain human-dependent, laborious, and costly. | Limits scalability, increases development time, high operational costs. | Prompt engineering for LLMs, manual KG construction/validation, gold-standard dataset creation. |
| Human-AI Knowledge Gap | AI’s internal representations or reasoning diverge from human understanding. | Leads to miscommunication, distrust, ineffective collaboration. | LLMs favoring internal knowledge, AI-discovered concepts in AlphaZero, ML models lacking scientific insight. |
| Prior Biases | Human pre-existing beliefs influence interpretation or guidance. | Can impede adoption of AI insights, introduce unwanted bias. | Chess grandmasters’ resistance to AlphaZero’s unconventional moves. |
| Divergent Objectives | AI optimizes for different goals than humans. | Mismatch in priorities leads to unexpected/undesirable outcomes. | AI seeking pure win probability vs. human seeking robust/simpler solutions. |
| Computational Capacities | AI’s superior processing leads to insights humans perceive as “risky.” | Limits human comprehension, impacts trust and adoption. | AI moves humans perceive as “risky” due to their limited cognitive budget. |
| Scaling Human Supervision | Difficulty in providing effective guidance to increasingly powerful AIs. | Weak-to-Strong generalization challenges, humans struggle to audit. | Auditing large LLMs, providing feedback for complex AI systems. |
| Resolving Conflicts | Handling conflicting inputs from multiple human experts or AI. | Leads to inconsistencies, impacts decision-making. | Aggregating expert opinions for KG validation, LLM knowledge conflicts. |
| Maintaining Trust & Interpretability | Opacity of AI systems hinders human understanding. | Reduces user confidence, impedes debugging, limits responsible use. | Black-box LLMs, uninterpretable prompts, lack of provenance. |
This section synthesizes frameworks, algorithms, and applications that either leverage or confront the complexities of human-in-the-loop (HIL) processes and human-AI collaboration (HAC), critically assessing their assumptions, architectural choices, and their efficacy in bridging the inherent “human-AI knowledge gap.”
The foundational role of human expertise is undeniable across various stages of knowledge acquisition. In many domains, initial tasks such as prompt engineering and data curation remain predominantly human-dependent, acting as a significant bottleneck. For instance, creating high-quality prompts is consistently described as “time-consuming and laborious” and requiring “significant human expertise and effort” for eliciting knowledge from Large Language Models (LLMs) [12,18,20,43,52]. Similarly, the construction of Knowledge Graphs (KGs) heavily relies on manual efforts for source selection, ontology development, mapping definition, and validation [3,48,74]. The creation of gold-standard datasets for diverse tasks, including Named Entity Recognition (NER) and Relation Extraction (RE), also necessitates “meticulous manual annotation by experts” [16,21,25,48,75].
Human-in-the-loop approaches are instrumental in refining automated systems, validating extracted knowledge, and addressing subtle errors. Frameworks like StructSense explicitly integrate HIL mechanisms to ensure the quality and validation of structured information extraction, where a “feedback agent” allows users to correct LLM outputs or provide natural language guidance, significantly enhancing reliability and trustworthiness [70]. This human oversight is particularly crucial in ambiguous tasks where it provides “critical disambiguation and grounding” [70]. In KG validation, human experts are called upon to review flagged statements or ambiguities identified by LLM validators, ensuring accuracy in vast knowledge repositories [40,55]. LLM memory-enhanced methods such as TeachMe and MemPrompt directly incorporate human feedback for refining LLM knowledge, allowing users to “check its facts and reasoning and correct it when it is wrong” [20,75]. Furthermore, the “meticulously crafted fine-tuning data” provided by humans plays a crucial role in activating and utilizing a Pre-trained Language Model’s (PLM) parametric knowledge, underscoring continued human dependence in bridging the utilization gap, particularly in Supervised Fine-Tuning (SFT) and Reinforcement Learning from Human Feedback (RLHF) paradigms [53].
Beyond mere validation, HIL strategies enhance interpretability and steerability. Language Bottleneck Models (LBMs) are designed to provide summaries that are “readable and editable by domain experts,” allowing educators to “prompt engineer the encoder” and integrate human preferences via reward signals to shape the AI’s pedagogical behavior and knowledge extraction processes [50]. Concept Bottleneck LLMs (CB-LLMs) offer “concept-level intervention,” enabling users to directly “steer” model behavior by modifying concept activations, demonstrated in applications like bias removal and toxicity reduction [32]. Similarly, AutoElicit simplifies expert prior elicitation by allowing human experts to “provide knowledge as natural language” and “steer LLMs away from unwanted bias through task descriptions” [19]. Explainable AI (XAI) also seeks to bridge comprehension gaps by presenting AI system predictions in a “human-understandable form” [29].
While HIL and HAC offer substantial benefits, they introduce their own set of challenges and trade-offs. The primary concern is the resource constraint and manual effort associated with human involvement, which can be time-consuming, laborious, and costly [9,20,72]. StructSense, while improving performance, noted that HIL “consistently increased operational cost and token usage” and introduced “additional processing overhead” [70]. Scalability remains an issue, as crowdsourcing is often limited to “simple and well-defined tasks,” struggling with more diverse and specific data [72]. Furthermore, human biases can inadvertently be introduced through manual editing or feedback, and inconsistencies can arise when aggregating input from multiple experts [33,50].
The “human-AI knowledge gap” is a persistent and multifaceted challenge. It manifests when knowledge is either unknown to both human and machine (“UH, UM” necessitating collaboration) [30] or when AI’s internal representations diverge significantly from human understanding. In robotics, this translates to a severe “knowledge bottleneck,” where “knowledge has to be provided by a human” due to safety risks, data scarcity, and the inherent difficulty of programming Human-Robot Interaction (HRI) for unpredictable human behaviors [64]. LLMs frequently exhibit this gap by “sometimes favour their internal knowledge rather than the provided context,” leading to “knowledge conflicts” and an “interpretability gap” [20]. Similarly, the “ineffective knowledge utilization” of complex human-curated factual knowledge bases by AI systems highlights a disconnect between human-designed structures and AI processing capabilities [7]. In specific scientific domains, ML models may achieve high predictive performance but fail to provide scientific insights “understandable by domain experts and policymakers,” leading to a “stakeholder interest gap” where valuable AI outputs are not effectively integrated into human decision-making and scientific inquiry [39]. The large_knowledge_model_perspectives_and_challenges paper also notes a “cognitive gap” between LLM knowledge storage and human associative thinking.
A pivotal study on AlphaZero’s concept transfer to chess grandmasters offers deep insights into the human-AI knowledge gap and its complexities [54]. This work highlights several human-AI discrepancy challenges:
- Human Prior Biases: Grandmasters possess pre-existing biases that can conflict with AlphaZero’s “unconventional” but optimal strategies.
- Divergent Objectives: AI systems are often optimized for specific goals (e.g., optimal play), while humans might prioritize practical, safer, or less complex solutions.
- Differing Computational Capacities: AI’s superior computational power allows for moves that humans perceive as “risky” due to their own limited cognitive budget.
- Human “Overthinking”: Experts might identify an AI’s optimal move but ultimately choose a different one, influenced by familiar heuristics or a reluctance to deviate from established principles. While the grandmasters improved their performance, demonstrating successful collaboration and an effort to bridge the “M-H set” (machine-unique knowledge unknown to humans), the study revealed that bridging this gap is not merely about knowledge transfer, but also about managing fundamental cognitive and objective differences [54].
Current “bridging” efforts primarily focus on managing the human-AI knowledge gap rather than fully closing it. This often involves optimizing human interaction, enhancing AI interpretability, and providing structured feedback mechanisms. PU-ADKA, for instance, focuses on “cost-efficient expert involved interaction” in sensitive domains by accurately matching questions to experts based on “knowledge boundary” estimates, thereby optimizing human resource allocation [4]. Active Learning (AL) explicitly integrates human experts as an “oracle” to label “uncertain predictions,” optimizing the interaction between automated systems and human expertise to overcome the annotation bottleneck in relation extraction [6]. The implicit incorporation of “human common knowledge” through pre-trained LLMs, as seen in Pluvio for assembly code analysis or in GLM’s reliance on human-curated KGs like ConceptNet, represents a form of indirect human expertise leverage, where foundational models learn from vast human-generated text and data, rather than requiring direct, continuous interaction [24,42,63].
Looking forward, several areas warrant critical assessment and further research. A significant challenge lies in scaling human supervision and input for increasingly powerful AI models, particularly in the context of “Weak-to-Strong generalization,” where humans may struggle to provide effective guidance to AIs that far exceed their capabilities [12]. Resolving conflicting inputs from multiple human experts and dynamically learning from continuous corrections remain open questions for interactive systems like LBMs [50]. There is also a need for intelligent interfaces and formalisms to efficiently integrate human expert confidence and subjective judgments for uncertainty resolution in KGs [55]. Ultimately, the goal is to design ML systems that actively facilitate the co-creation of knowledge between AI and human experts, enabling iterative refinement of both models and scientific theories, rather than merely using humans for validation or data provision [39]. The shift is towards AI systems that can proactively “ask clarifying questions” from human experts when uncertain, suggesting a more symbiotic future for human-AI collaboration [17].
7.5 Ethical and Societal Implications
The rapid advancements in knowledge acquisition (KA) are accompanied by a growing imperative to critically assess their ethical and societal implications.
Ethical and Societal Implications of Knowledge Acquisition
| Ethical/Societal Challenge | Description / Manifestation | Impact of Knowledge Acquisition | Mitigations / Responsible AI Practices |
|---|---|---|---|
| Reliability & Misinformation | LLM hallucinations, factual inconsistency, “utilization gap.” | Spreads incorrect information, undermines trustworthiness. | KG grounding, HIL, traceability, accountable reasoning, transparent LLM limits. |
| Bias & Fairness | LLM biases from training data, human input biases, proxy data biases. | Perpetuates stereotypes, leads to unfair/skewed outcomes. | Bias-aware KG construction, uninformative priors, concept unlearning, data cleaning. |
| Privacy & Intellectual Property | Verbatim memorization, model extraction, data leakage. | Unauthorized copying, IP theft, privacy violations. | Strict licensing, data de-identification, privacy-preserving training, secure deployment (on-premises LLMs, sandboxing). |
| Safety | Imperfect learned behaviors in physical systems. | Physical harm to robots/humans, unsafe decision-making. | Prioritizing traditional planning methods for safety-critical tasks, robust RL. |
| Sustainability | High computational resources/energy for training large models. | Environmental impact, economic burden for continuous updates. | “Green AI” research, resource-efficient models. |
| Human Over-Reliance | Humans accepting AI outputs uncritically, stifling creativity. | Reduced critical thinking, potential for manipulation. | Transparent communication of AI limitations, encouraging human agency, interdisciplinary research. |
| Knowledge Inequality | AI insights accessible only to a few. | Exacerbates societal disparities, limits broader benefit. | Democratizing access to scientific information, open-source AI. |
| Job Displacement | Automation of knowledge engineering tasks. | Socio-economic disruption, need for reskilling. | Policy discussions, focus on human-AI augmentation. |
| Reproducibility | Lack of reproducibility in sensitive AI applications. | Undermines trust, hinders verification, ethical concerns. | Standardized benchmarks, open data, transparent methods. |
This section synthesizes key ethical challenges and opportunities presented by large-scale automated KA, spanning reliability, bias, privacy, intellectual property, safety, and responsible deployment across diverse domains.
A primary concern centers on the reliability, trustworthiness, and mitigation of misinformation generated by knowledge-intensive AI systems. Large Language Models (LLMs) are notoriously susceptible to “hallucinations,” producing factually incorrect but convincing information, which poses a significant ethical challenge when these models are employed for scientific data dissemination or general knowledge provision [2,12,20]. The observed failure of Meta AI’s Galactica LLM due to critical feedback underscores the importance of reliability and avoiding misinformation [2]. Similarly, the “knowledge acquisition-utilization gap” and “unreliability of parametric knowledge” in pre-trained language models (PLMs) raise concerns about factual inconsistency and the potential to generate misinformation [53]. To counter these issues, several approaches emphasize transparent and grounded knowledge. Knowledge Graphs (KGs) are crucial for providing factual grounding, enhancing trustworthiness, and mitigating hallucinations by enabling structured consistency and logical validation [1,3,12,17,31,36]. The integration of human-in-the-loop (HIL) components, such as StructSense’s feedback agent, directly enables humans to mitigate hallucinations and ensure reliability [70]. Furthermore, traceability through provenance tracking [52,55] and explicit justifications for KG edits enhance auditing and trust in AI-curated knowledge bases [17]. The commitment to “Accountable Reasoning” within Large Knowledge Models further advocates for reliable and interpretable outputs, which is an ethical imperative for responsible AI deployment [12].
Bias and fairness represent another pervasive ethical challenge. Bias can originate from various stages of knowledge acquisition. LLMs are inherently susceptible to biases (e.g., gender bias) embedded within their vast training datasets [12,20,30,40,55]. Critically, LLM-elicited knowledge, used to generate priors in predictive modeling, can also inadvertently contain and propagate these unwanted biases [19]. When human-provided knowledge is relied upon, biases from human input can also be introduced, as seen in robotic learning where “reward hacking” can lead to undesirable learned behaviors [64]. Bias can also arise from the construction of knowledge bases, where biased relationships or underrepresented concepts in graph structures can lead to skewed outcomes [3,7,33,71]. Implicit biases can manifest from incomplete or low-quality data sources during Knowledge Graph construction [3,9]. Furthermore, the use of proxy data, such as Night-Time Lights for wealth estimation, can introduce biases by underperforming in vulnerable regions, impacting socio-economic analysis and potentially leading to misallocation of resources [39]. Mitigation strategies for bias include developing bias-aware graph construction techniques [71], employing uninformative priors for sensitive features, and allowing experts to steer LLMs away from bias through refined task descriptions [19]. Concept Unlearning in Concept Bottleneck LLMs (CB-LLMs) offers a technical solution to remove or deactivate biased concepts, thereby enhancing prediction fairness [32]. Data cleaning, comprehensive quality measures, and a focus on “consistent algorithmic approaches to mitigate human biases” are vital for KGs to prevent bias propagation [3,31].
Privacy and intellectual property (IP) concerns are paramount in automated KA. Processes like web harvesting can raise implicit IP infringement issues [9]. More significantly, the verbatim memorization of training data by LLMs poses direct legal and copyright risks [60]. Model Extraction Attacks (MEAs) against proprietary AI models, particularly those offered as Machine Learning as a Service (MLaaS), represent a severe threat, enabling unauthorized copying and intellectual property theft, and potentially allowing adversaries to infer characteristics of the original training data [15,45]. LLMs also present privacy vulnerabilities by potentially leaking sensitive information [30,40]. To address these, measures include strict licensing compliance for data scraping [31], data de-identification in sensitive datasets like Electronic Health Records [21], and the development of privacy-preserving training methods and machine unlearning techniques [20,30,60]. Secure deployment strategies for LLMs, such as on-premises models, secure Retrieval-Augmented Generation (RAG), sandboxing, data anonymization, PII scrubbing, differential privacy, access control, encryption, and red-teaming, are essential for protecting sensitive organizational data and mitigating risks in mission-critical industries [48]. Local deployment of open-source LLMs can also safeguard data privacy by avoiding reliance on external proprietary API services [61]. RAG is further noted for its inherent compliance with privacy and copyright standards by querying external, authorized knowledge bases [12].
Responsible deployment and broader societal impact encompass a wide range of considerations. Safety is paramount, particularly in robotics, where imperfect learned behaviors can lead to physical harm to robots, objects, or humans, necessitating a preference for traditional, safety-guaranteed planning methods in safety-critical tasks [29,64]. In sensitive domains like healthcare or financial risk analysis, trustworthy and actionable knowledge is an ethical imperative, as inaccuracies or flawed insights can have severe societal consequences [3,39]. The sustainability of AI, often termed “Green AI,” is another significant ethical concern, given the substantial computational resources and energy consumption associated with training and continuously updating large models [20,40,51,64]. The ethical implications of human-AI interaction include the potential for human over-reliance on AI-generated knowledge, where human creativity or critical thinking might be stifled, as seen in the reactions of chess grandmasters to AlphaZero’s unconventional moves [54,64]. This concern highlights the need for AI systems to transparently communicate their knowledge limitations to ensure social acceptance [53]. Furthermore, the impact on human expertise, particularly the risk of “knowledge inequality” if AI insights are only accessible to a select few, warrants careful consideration [54].
The “arms race” aspect in AI security manifests through adversarial knowledge acquisition. Open knowledge acquisition systems are vulnerable to malicious actors who might spread “fake news” or engage in sabotage [55]. The internal mechanisms of LLMs can be exploited for malicious purposes, leading to “jailbreak” attacks that bypass safety alignment and generate toxic content or release private information [30]. In contrast, knowledge acquisition frameworks also offer significant positive societal impacts, such as democratizing access to scientific information and advanced problem-solving strategies [2,33,36,38,45]. They can accelerate scientific discovery, as exemplified by enhancing LLMs for critical healthcare areas like drug discovery [4], support poverty reduction initiatives through improved data analysis [39], and bolster cybersecurity by detecting intellectual property infringements and vulnerability propagation through code reuse [24]. However, the potential for job displacement and the commoditization of expert knowledge due to automated Knowledge Engineering tasks also represent notable socio-economic implications [33,52]. A lack of reproducibility in sensitive domains like health is also identified as an ethical concern, risking the trustworthiness of AI systems where verification is critical [74].
Despite acknowledging these ethical considerations, many papers primarily focus on technical performance, often outlining concerns at a high level or inferring them from technical challenges, rather than providing explicit methods, safeguards, or detailed ethical frameworks for mitigation [2,5,7,29,38,46,54,58,59,64]. There remains a critical need for interdisciplinary research avenues combining technical solutions with robust ethical guidelines and human-centered design. Future work must integrate auditing mechanisms and ethical guidelines into KA pipelines to actively detect and rectify biases from training data or malicious inputs [55]. AI systems should be architected to encourage critical evaluation and human agency rather than fostering blind acceptance of AI-derived knowledge [54]. This includes the challenge of defining and operationalizing “sophisticated ethics knowledge bases” and knowledge alignment technologies to effectively capture and enforce complex ethical considerations across diverse scenarios and moral dilemmas [12,30]. The ongoing “arms race” in AI security, particularly against model extraction, necessitates continued research into defensive mechanisms, along with clear ethical guidelines for vulnerability disclosure and legal frameworks for intellectual property in AI models [15,45]. Overall, ensuring that KA advancements serve humanity responsibly requires a concerted effort to weave technical robustness with social, legal, and ethical safeguards across all AI applications [4,15,19,39,54,64].
7.6 Emerging Trends and Research Opportunities
The landscape of knowledge acquisition in artificial intelligence is undergoing a significant transformation, driven by advancements in Large Language Models (LLMs) and the increasing demand for robust, interpretable, and continuously evolving AI systems. Current research highlights critical limitations and opens avenues for novel interdisciplinary approaches, systematic evaluation, and innovative technical solutions.
A primary challenge lies in understanding and managing the intrinsic knowledge within LLMs. Studies reveal issues such as knowledge entropy decay during pre-training, which hinders new knowledge acquisition, and the problem of catastrophic forgetting during continual learning [34,69]. This necessitates the development of sophisticated continual learning strategies, including data curriculums, knowledge augmentation for reactivating long-tail knowledge, and data replay interventions to maintain knowledge circuit elasticity and plasticity [34,68]. Furthermore, a persistent “utilization gap” exists, where LLMs acquire knowledge but fail to apply it effectively in downstream tasks, particularly concerning procedural and task knowledge beyond mere encyclopedic facts [53,73]. Future research must focus on crafting fine-tuning data to specifically enhance utilization efficiency, especially for smaller models, and investigating knowledge capacity scaling laws to understand the interplay between model size, data signal-to-noise ratio, and knowledge acquisition capability [34,53].
The integration of LLMs with external, structured knowledge sources, particularly Knowledge Graphs (KGs), forms a critical and rapidly advancing area, often termed neuro-symbolic AI [12,29,30,36,58]. This approach aims to augment LLMs’ parametric knowledge, mitigate issues like outdated information and hallucinations, and provide verifiable, interpretable reasoning. Opportunities include developing more architectural and learning strategies for organizing knowledge within LLMs, refining KG construction techniques to handle uncertainty, granularity, and mixed data types, and implementing dynamic KG updating and evolution mechanisms [3,31,51,55]. Specifically, advancements in prompt generation can inform more efficient active learning acquisition functions. For instance, the systematic optimization of prompts can significantly improve knowledge elicitation from LLMs, as demonstrated by techniques like AutoPrompt, which explore discrete prompt spaces for optimal performance [43]. This can be extended to guide active learning by generating contextually relevant queries that maximize information gain, thereby enhancing acquisition functions and reducing data dependency [13,50]. The application of graph-based methods can also profoundly improve LLM knowledge representation, particularly within Retrieval-Augmented Generation (RAG) systems. Research focuses on advanced graph construction, dynamic and multi-modal graphs, scalable graph retrieval, and adaptive prompts that align with LLM’s pre-trained knowledge to navigate complex graph structures [1,71]. This synergy addresses the LLMs’ struggle with structural comprehension and noisy contexts [20,27].
Human-in-the-Loop (HIL) systems and expert interaction are crucial for cost-efficient knowledge acquisition, especially in sensitive and specialized domains. Future work involves refining expert integration, such as fine-tuning LLMs on relevant literature and using chain-of-thought elicitation to make LLM-derived priors more transparent [19]. Active learning strategies, from targeted re-annotation to advanced uncertainty quantification, remain central to reducing manual effort and improving data efficiency [15,25,45,57]. The creation of new benchmarks, such as CKAD, designed for cost-efficient expert-involved interaction, is vital for fostering innovation in this area [4].
A paradigm of persistent learning is emerging, emphasizing lifelong knowledge management, dynamic knowledge transfer, and automation. This involves overcoming learning gaps and supporting continuous knowledge curation, updating, and justification [8,14,17,60]. Research into dynamic knowledge state modeling for continuous learning and forgetting, as well as developing active sensing capabilities to select information-maximizing questions, is crucial [22,50]. The need for automation is underscored by efforts like Bench4KE, which aims to benchmark automated competency question generation, highlighting the drive to reduce manual effort in knowledge engineering [14]. Similarly, dynamic knowledge transfer is critical for lifelong learning systems, which require mechanisms to efficiently share and reuse knowledge across tasks and domains, moving beyond static knowledge bases [33,37,62,64].
Interdisciplinary research is increasingly vital for attacking the Knowledge Acquisition Bottleneck (KAB). Insights from cognitive science, neuroscience, and psychology can inform AI development, particularly in areas like memory consolidation, learning strategies, and metacognition [26,30,56,58,67,72]. For instance, the information bottleneck principle, exemplified by InfoBot, offers a framework for disentangled representations and skill discovery, drawing parallels to cognitive processes [24,35,56]. Moreover, novel learning paradigms are essential to address “current and future challenges in knowledge representation and reasoning” and the need for “machine learning for world knowledge acquisition or organization” [29,72]. This includes developing neuro-symbolic systems that integrate deep learning with explicit symbolic reasoning, exploring quantum learning concepts for transferable knowledge representations, and focusing on commonsense acquisition [28,37].
Robust evaluation and standardized benchmarks are paramount for measuring progress and bridging the research-practice gap. There is a critical need for comprehensive, real-time benchmarks that can assess dynamic world knowledge, moving beyond static evaluations [3,20,64,74]. Developing improved metrics for semantic plausibility, conceptual alignment, and evaluating the effectiveness of solutions in industry contexts is crucial [39,70,75].
Considering these trends and challenges, we propose several innovative research agendas:
-
Innovative Solution 1: Adaptive Knowledge Bottleneck Orchestration for Resource-Aware and Interpretable AI. This agenda proposes a meta-learning framework capable of dynamically modulating the “knowledge bottleneck” within AI systems. Inspired by InfoBot’s $\beta$ parameter for balancing compression and interpretability [56] and Language Bottleneck Models’ (LBMs) natural-language summaries [50], this framework would adaptively adjust information flow based on task criticality, computational budget, real-time data, and human auditability requirements. For example, in safety-critical autonomous systems, the internal causal knowledge bottleneck could be tightened for high interpretability, potentially increasing computational cost. Conversely, for exploratory data analysis, it could be loosened for rapid pattern discovery. This interdisciplinary approach, integrating meta-learning, resource optimization, and human-computer interaction, aims to create ‘metacognitive’ AI systems that optimize both performance and trustworthiness.
-
Innovative Solution 2: Generative Lifelong Knowledge Ledger with Human-in-the-Loop Refinement. This solution envisions a comprehensive system for lifelong knowledge acquisition by extending LBMs’ interpretable natural-language summaries [50] into a “living knowledge ledger.” This ledger would continuously track acquired, modified, forgotten, and consolidated information, complete with timestamps and provenance, akin to human memory processes of forgetting and consolidation [33,67]. Drawing inspiration from InfoBot’s identification of critical “decision states” for exploration [56], the system would actively identify “knowledge inflection points” where new data mandates significant updates. Generative AI would synthesize new hypotheses, generate targeted diagnostic questions to resolve ambiguities (bridging learning gaps identified in FictionalQA [60]), and provide natural-language explanations for knowledge updates or obsolescence. This human-auditable and continuously evolving knowledge base would address the dynamism of real-world information and ensure human trust and intervention through transparent knowledge management.
-
Innovative Solution 3: Natural Language-Driven Hierarchical Policy Synthesis with Explainable Decision Points for Embodied AI. This framework combines advanced natural language understanding with hierarchical reinforcement learning (HRL) for embodied AI, such as robotics [64]. Human experts would provide high-level goals and safety constraints in natural language. An LBM-like component [50] would process these linguistic inputs to derive an interpretable, structured representation of human intent, guiding an InfoBot-inspired HRL agent [56] to discover optimal policies by efficiently exploring decision states relevant to human-specified subgoals. Crucially, the system would generate natural language explanations for its chosen decision states or sub-policies, and how these actions contribute to the high-level human goal. This bidirectional communication bridges the human-AI knowledge gap, makes complex RL policies auditable, and allows for efficient, human-steered knowledge acquisition in complex robotic tasks by providing rich feedback loops beyond sparse rewards [20,24,46].
These research directions collectively underscore a paradigm shift towards more adaptive, interpretable, and human-aligned AI systems that can continuously acquire, evolve, and manage knowledge in complex and dynamic environments, addressing the KAB through interdisciplinary innovation and rigorous evaluation.
8. Conclusion
The persistent challenge of the knowledge acquisition bottleneck (KAB) has been a central theme in artificial intelligence research, fundamentally hindering the development of robust, generalizable, and trustworthy AI systems. This survey has explored the diverse frameworks, algorithms, and applications designed to mitigate this bottleneck, revealing significant progress driven by the synergistic integration of Large Language Models (LLMs), Knowledge Graphs (KGs), and sophisticated learning paradigms. The KAB, broadly characterized by the immense manual effort required for data annotation and expert knowledge elicitation, data scarcity, and issues with knowledge fragility and utilization, has necessitated innovative solutions across various domains [9,10,16,25].
Significant breakthroughs have emerged from leveraging the inherent knowledge within LLMs and augmenting it with structured information. LLM-centric approaches have notably enhanced knowledge acquisition and utilization. Frameworks like DKA have demonstrated the effectiveness of disentangled knowledge acquisition and LLM feedback for complex tasks such as Knowledge-based Visual Question Answering (KVQA), achieving state-of-the-art performance with minimal demonstration examples [61]. Similarly, Self-Tuning introduces a “self-teaching” paradigm, enabling LLMs to acquire new knowledge effectively from raw documents by augmenting self-supervised, knowledge-intensive tasks, thereby addressing the KAB in dynamic knowledge environments [68]. R1-Searcher++ further advances dynamic knowledge acquisition by allowing LLMs to seamlessly integrate and alternate between internal knowledge and external retrieval, continuously enriching their knowledge base through a two-stage training strategy incorporating reinforcement learning [27]. AutoElicit has successfully employed LLMs to automatically elicit informative prior distributions for predictive models, drastically reducing the knowledge acquisition burden in data-scarce and sensitive domains like healthcare by saving substantial labeling effort [19]. For interpretability, Concept Bottleneck Large Language Models (CB-LLMs) offer a novel framework for creating inherently interpretable LLMs that match or outperform traditional black-box models while providing faithful and human-understandable interpretations, bypassing the data annotation bottleneck through automatic concept generation [32]. Language Bottleneck Models (LBMs) extend this by reframing knowledge tracing as an inverse problem, inferring interpretable natural-language knowledge states with superior data efficiency and human steerability [50]. Insights into LLM internal dynamics, such as the decay of knowledge entropy during pretraining, underscore the challenge of new knowledge acquisition and forgetting, suggesting optimal balance points for plasticity and stability [69].
In parallel, advancements in Knowledge Graph (KG) construction and Information Extraction (IE) have directly tackled the KAB by automating the creation and management of structured knowledge. KGValidator leverages LLMs to automate the validation of KG completion models, significantly reducing the cost and time of manual annotation under the Open-World Assumption [40]. SAC-KG employs LLMs as “skilled automatic constructors” for domain-specific KGs, mitigating contextual noise and hallucination through iterative generation, verification, and pruning, achieving high precision and domain specificity without labeled data [66]. Tools like SciNLP-KG and MatSKRAFT demonstrate the feasibility of end-to-end automated extraction of scientific knowledge from unstructured and semi-structured texts, facilitating the rapid construction of large-scale KGs in specialized domains like NLP research and materials science, often outperforming LLMs in accuracy and computational efficiency for structured data extraction [11,65]. The concept of generative KGC further aims to overcome the traditional pipeline’s error propagation and poor adaptability by utilizing sequence-to-sequence models [23].
A particularly promising direction lies in hybrid neuro-symbolic approaches, which synergistically combine the strengths of LLMs and KGs. The vision of a “Large Knowledge Model” (LKM) emphasizes the deep integration of KGs to augment LLM pretraining, mitigate hallucination, and enhance reasoning, while LLMs concurrently bolster traditional KG technology through instruction-driven extraction and reasoning capabilities [12,36]. Methods like TeKGen verbalize entire KGs into synthetic corpora to overcome the architectural mismatch between structured and unstructured data, leading to improved factual accuracy in language models [1]. Retrieval-Augmented Generation (RAG) systems, especially those incorporating graph-based techniques, have shown superior performance in leveraging external knowledge for LLM reasoning and question answering, demonstrating how LLMs can effectively interact with large KGs for structured exploration and pruning [63,71].
Furthermore, advancements in data-centric and learning paradigms have directly addressed the KAB. Active Learning (AL) frameworks, such as Deep Bayesian Active Learning (DAL), consistently outperform passive learning by reducing data scarcity and manual effort in NLP tasks, offering robust strategies for efficient annotation [57]. The significance of high-quality annotation has been underscored, with studies showing substantial performance drops when models are trained on single-annotated data versus multiple-annotated data, leading to the development of data-centric ranking approaches for targeted re-annotation [25]. Frameworks like Net2Net accelerate learning by transferring knowledge from smaller, pre-trained networks to larger ones, reducing training costs and facilitating lifelong learning [62]. Cognitive-inspired mechanisms of forgetting and consolidation provide a principled way to manage evolving knowledge bases, addressing the “Stability-Plasticity dilemma” in incremental acquisition systems [67]. The Information Bottleneck principle has been instrumental in developing efficient learning and exploration strategies, enabling agents to learn default behaviors and disentangled skills in sparse reward environments [24,35,56].
Despite these impressive strides, several overarching challenges persist. The data scarcity and data quality issues remain critical, particularly in specialized or low-resource domains, hindering reproducibility and generalizability [48,74]. Scalability and computational costs continue to be bottlenecks, especially for extremely large KGs and advanced LLM deployments, alongside the need for efficient incremental updates and quality assurance in KG construction [3,40]. The fundamental problem of interpretability and explainability persists, particularly for LLMs that often lack accuracy in specific domains and numerical facts and do not provide provenance or reliability information, limiting their adoption in high-stakes applications and scientific discovery [39,55]. The robustness and generalizability of models, especially when confronted with out-of-distribution (OOD) data or domain-specific jargon, remain significant concerns, highlighting the severe generalizability limitations of many off-the-shelf NLP tools [48]. The “knowledge acquisition-utilization gap,” where models fail to effectively apply a substantial portion of the knowledge they possess, and the “knowledge complexity mismatch” between LLMs and intricate knowledge bases, indicate deeper issues in knowledge representation and processing [7,53]. Addressing LLM hallucination and bias is also paramount for developing trustworthy AI systems [52]. Finally, the lack of standardized evaluation metrics and benchmarks for automated knowledge engineering tasks makes rigorous comparative analysis challenging [14,74].
Looking ahead, the future landscape of knowledge acquisition research is poised for transformative advancements. A deeper and more sophisticated neuro-symbolic integration remains a crucial frontier, moving towards models that can seamlessly bridge sub-symbolic learning with explicit symbolic reasoning for greater understanding and control [12,36]. Emphasis will be placed on dynamic, continual, and adaptive learning systems that can efficiently align with ever-changing world knowledge, manage knowledge conflicts, and learn from experience across diverse tasks and domains, evolving cumulative intelligence rather than static snapshots [20,33,67]. Enhanced human-AI collaboration will be vital, with AI not merely as a tool but as a partner in knowledge discovery, requiring models that offer actionable scientific understanding and can even teach humans novel concepts [39,54,70]. Research will increasingly prioritize knowledge purity, transparency, and provenance, ensuring that acquired knowledge is accurate, auditable, and free from biases, moving towards “conceptual knowledge” and integrated uncertainty management [7,55]. The adoption of reference architectures and modular, open-source toolsets will be critical for standardizing knowledge engineering practices and fostering community engagement [3,59]. Finally, extending knowledge acquisition beyond textual data to multimodal inputs and developing embodied intelligence with self-evolving LLMs will pave the way for AI systems with a more profound understanding and interaction with the physical world [3,30]. These research avenues hold immense potential to unlock more reliable, interpretable, and truly intelligent AI systems, fundamentally transforming data science and AI.
# References
[1] Knowledge graph based synthetic corpus generation for knowledge-enhanced language model pre-training https://arxiv.org/abs/2010.12688
[2] Knowledge AI: Fine-tuning NLP Models for Facilitating Scientific Knowledge Extraction and Understanding https://arxiv.org/abs/2408.04651
[3] Construction of knowledge graphs: State and challenges https://arxiv.org/abs/2302.11509
[4] Active Domain Knowledge Acquisition with$100 Budget: Enhancing LLMs via Cost-Efficient, Expert-Involved Interaction in Sensitive Domains https://arxiv.org/abs/2508.17202
[5] Synthetic Knowledge Ingestion: Towards Knowledge Refinement and Injection for Enhancing Large Language Models https://arxiv.org/abs/2410.09629
[6] NLP-based Relation Extraction Methods in Requirements Engineering https://arxiv.org/abs/2401.12075
[7] Revisiting the knowledge injection frameworks https://arxiv.org/abs/2311.01150
[8] When Babies Teach Babies: Can student knowledge sharing outperform Teacher-Guided Distillation on small datasets? https://arxiv.org/abs/2411.16487
[9] Natural language processing for information extraction https://arxiv.org/abs/1807.02383
[10] A short survey on sense-annotated corpora https://arxiv.org/abs/1802.04744
[11] End-to-end nlp knowledge graph construction https://arxiv.org/abs/2106.01167
[12] Large knowledge model: Perspectives and challenges https://arxiv.org/abs/2312.02706
[13] Adaptive Elicitation of Latent Information Using Natural Language https://arxiv.org/abs/2504.04204
[14] Bench4KE: Benchmarking Automated Competency Question Generation https://arxiv.org/abs/2505.24554
[15] A framework for the extraction of deep neural networks by leveraging public data https://arxiv.org/abs/1905.09165
[16] Knowledge Efficient Deep Learning for Natural Language Processing https://arxiv.org/abs/2008.12878
[17] Evo-DKD: Dual-Knowledge Decoding for Autonomous Ontology Evolution in Large Language Models https://arxiv.org/abs/2507.21438
[18] GPT-3 Powered Information Extraction for Building Robust Knowledge Bases https://arxiv.org/abs/2408.04641
[19] AutoElicit: Using Large Language Models for Expert Prior Elicitation in Predictive Modelling https://arxiv.org/abs/2411.17284
[20] How do large language models capture the ever-changing world knowledge? a review of recent advances https://arxiv.org/abs/2310.07343
[21] HYPE: a high performing NLP system for automatically detecting hypoglycemia events from electronic health record notes https://arxiv.org/abs/1811.11945
[22] Modeling knowledge acquisition from multiple learning resource types https://arxiv.org/abs/2006.13390
[23] Generative knowledge graph construction: A review https://arxiv.org/abs/2210.12714
[24] Pluvio: Assembly clone search for out-of-domain architectures and libraries through transfer learning and conditional variational information bottleneck https://arxiv.org/abs/2307.10631
[25] Single versus multiple annotation for named entity recognition of mutations https://arxiv.org/abs/2101.07450
[26] Neural networks that overcome classic challenges through practice https://arxiv.org/abs/2410.10596
[27] R1-Searcher++: Incentivizing the Dynamic Knowledge Acquisition of LLMs via Reinforcement Learning https://arxiv.org/abs/2505.17005
[28] Classical planning in deep latent space https://arxiv.org/abs/2107.00110
[29] Current and future challenges in knowledge representation and reasoning https://arxiv.org/abs/2308.04161
[30] Knowledge mechanisms in large language models: A survey and perspective https://arxiv.org/abs/2407.15017
[31] Knowledge Graph Extension by Entity Type Recognition https://arxiv.org/abs/2405.02463
[32] Concept bottleneck large language models https://arxiv.org/abs/2412.07992
[33] Agent kb: Leveraging cross-domain experience for agentic problem solving https://arxiv.org/abs/2507.06229
[34] How do llms acquire new knowledge? a knowledge circuits perspective on continual pre-training https://arxiv.org/abs/2502.11196
[35] Unsupervised skill discovery with bottleneck option learning https://arxiv.org/abs/2106.14305
[36] Know: A real-world ontology for knowledge capture with large language models https://arxiv.org/abs/2405.19877
[37] Quantum learning and essential cognition under the traction of meta-characteristics in an open world https://arxiv.org/abs/2311.13335
[38] Deepke: A deep learning based knowledge extraction toolkit for knowledge base population https://arxiv.org/abs/2201.03335
[39] Satellite image and machine learning based knowledge extraction in the poverty and welfare domain https://arxiv.org/abs/2203.01068
[40] Kgvalidator: a framework for automatic validation of knowledge graph construction https://arxiv.org/abs/2404.15923
[41] Axcell: Automatic extraction of results from machine learning papers https://arxiv.org/abs/2004.14356
[42] Exploiting structured knowledge in text via graph-guided representation learning https://arxiv.org/abs/2004.14224
[43] Autoprompt: Eliciting knowledge from language models with automatically generated prompts https://arxiv.org/abs/2010.15980
[44] KnowMap: Efficient Knowledge-Driven Task Adaptation for LLMs https://arxiv.org/abs/2506.19527
[45] CEGA: A Cost-Effective Approach for Graph-Based Model Extraction and Acquisition https://arxiv.org/abs/2506.17709
[46] Information must flow: Recursive bootstrapping for information bottleneck in optimal transport https://arxiv.org/abs/2507.10443
[47] Knowledge as Invariance–History and Perspectives of Knowledge-augmented Machine Learning https://arxiv.org/abs/2012.11406
[48] Trusted Knowledge Extraction for Operations and Maintenance Intelligence https://arxiv.org/abs/2507.22935
[49] Better together: Enhancing generative knowledge graph completion with language models and neighborhood information https://arxiv.org/abs/2311.01326
[50] Language Bottleneck Models: A Framework for Interpretable Knowledge Tracing and Beyond https://arxiv.org/abs/2506.16982
[51] Lessons from Deep Learning applied to Scholarly Information Extraction: What Works, What Doesn’t, and Future Directions https://arxiv.org/abs/2207.04029
[52] Knowledge engineering using large language models https://arxiv.org/abs/2310.00637
[53] Measuring the knowledge acquisition-utilization gap in pretrained language models https://arxiv.org/abs/2305.14775
[54] Bridging the human-ai knowledge gap: Concept discovery and transfer in alphazero https://arxiv.org/abs/2310.16410
[55] Uncertainty Management in the Construction of Knowledge Graphs: a Survey https://arxiv.org/abs/2405.16929
[56] Infobot: Transfer and exploration via the information bottleneck https://arxiv.org/abs/1901.10902
[57] Deep bayesian active learning for natural language processing: Results of a large-scale empirical study https://arxiv.org/abs/1808.05697
[58] Metacognition in Content-Centric Computational Cognitive C4 Modeling https://arxiv.org/abs/2503.17822
[59] Standardizing knowledge engineering practices with a reference architecture https://arxiv.org/abs/2404.03624
[60] A Fictional Q&A Dataset for Studying Memorization and Knowledge Acquisition https://arxiv.org/abs/2506.05639
[61] Knowledge acquisition disentanglement for knowledge-based visual question answering with large language models https://arxiv.org/abs/2407.15346
[62] Net2net: Accelerating learning via knowledge transfer https://arxiv.org/abs/1511.05641
[63] GRAIL: Learning to Interact with Large Knowledge Graphs for Retrieval Augmented Reasoning https://arxiv.org/abs/2508.05498
[64] A Survey of Behavior Learning Applications in Robotics–State of the Art and Perspectives https://arxiv.org/abs/1906.01868
[65] MatSKRAFT: A framework for large-scale materials knowledge extraction from scientific tables https://arxiv.org/abs/2509.10448
[66] Sac-kg: Exploiting large language models as skilled automatic constructors for domain knowledge graphs https://arxiv.org/abs/2410.02811
[67] Forgetting and consolidation for incremental and cumulative knowledge acquisition systems https://arxiv.org/abs/1502.05615
[68] Self-tuning: Instructing llms to effectively acquire new knowledge through self-teaching https://arxiv.org/abs/2406.06326
[69] Knowledge entropy decay during language model pretraining hinders new knowledge acquisition https://arxiv.org/abs/2410.01380
[70] STRUCTSENSE: A Task-Agnostic Agentic Framework for Structured Information Extraction with Human-In-The-Loop Evaluation and Benchmarking https://arxiv.org/abs/2507.03674
[71] Graph-based Approaches and Functionalities in Retrieval-Augmented Generation: A Comprehensive Survey https://arxiv.org/abs/2504.10499
[72] Machine learning with world knowledge: The position and survey https://arxiv.org/abs/1705.02908
[73] Physics of language models: Part 3.1, knowledge storage and extraction https://arxiv.org/abs/2309.14316
[74] A decade of knowledge graphs in natural language processing: A survey https://arxiv.org/abs/2210.00105
[75] Logical reasoning over natural language as knowledge representation: A survey https://arxiv.org/abs/2303.12023